Este artigo foi publicado como parte do Data Science Blogathon

Introdução
Aprendizagem. A regressão logística é geralmente usada quando temos que classificar os dados em duas ou mais classes. Um é binário e o outro é regressão logística multi-classe. Como o nome sugere, a classe binária tem 2 classes que são Sim / Não, Verdade / Falso, 0/1, etc. Na classificação de múltiplas classes, há mais de 2 Classes para classificar dados. Mas, antes de sairmos, Vamos primeiro definir a regressão logística:
“Regressão logística é um algoritmo de classificação para variáveis categóricas como Yes / Não, Verdade / Falso, 0/1, etc.”
Como é diferente da regressão linear??
Você também pode ter ouvido falar de regressão linear. Deixe-me dizer-lhe que há uma grande diferença entre regressão linear e regressão logística.. A regressão linear é usada para gerar valores contínuos, como o preço da casa, Receita, A população, etc. Na regressão logística, Geralmente calculamos a probabilidade que se encontra entre o intervalo 0 e 1 (Ambos inclusivos). Então a probabilidade pode ser usada para classificar os dados. Por exemplo, se a probabilidade calculada for superior a 0,5, em seguida, os dados pertenciam à classe A e, pelo contrário, por menos de 0,5, os dados pertenciam à classe B.
Mas minha pergunta é se ainda podemos usar a regressão linear para classificação.. Minha resposta será "Sim!! Por que não? Mas com certeza é uma ideia absurda.". Minha razão será que você pode atribuir um valor limite para regressão linear, quer dizer, se o valor previsto for superior ao valor limite, pertenciam à classe A; pelo contrário, para a classe B. Mas vai dar um grande erro e um modelo pobre com baixa precisão, que realmente não queremos. Direita? Sugiro que você use apenas algoritmos de classificação.
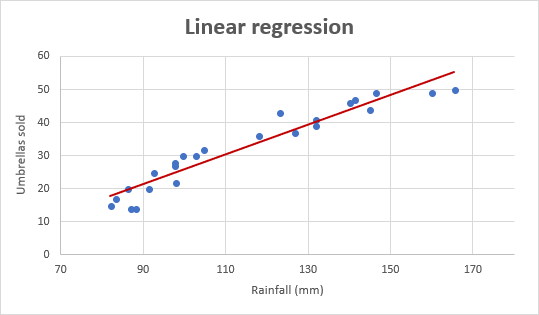
Agora vamos olhar para o gráfico de regressão linear mostrado abaixo.
(Cortesia: https://www.ablebits.com/)
O gráfico é uma linha reta que passa por alguns pontos, pois sempre evitamos curvas de overfit e incompatibilidade..
Agora vamos dar uma olhada no gráfico de regressão logística:
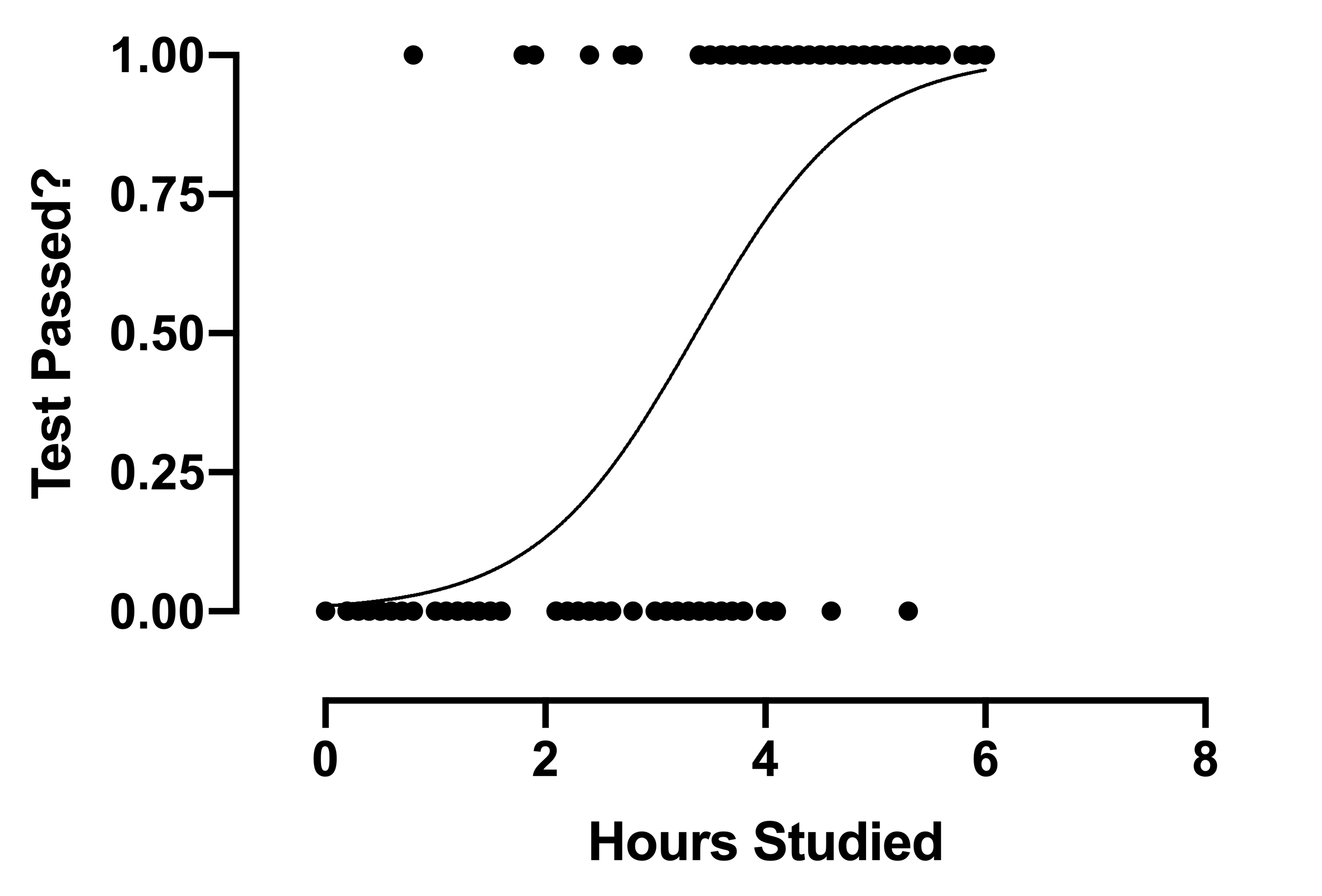
O gráfico é uma linha curva em vez de uma linha reta, Ao contrário da regressão linear.
Esta é uma grande diferença entre os dois tipos de regressão que acabamos de falar.. Então minha próxima pergunta é.
Por que temos uma linha curva para regressão logística em vez de uma linha reta?
Para responder a esta pergunta, Vamos caminhar um pouco através da regressão linear e a partir daí vamos chegar à curva de regressão logística. Está okey? Vamos começar.
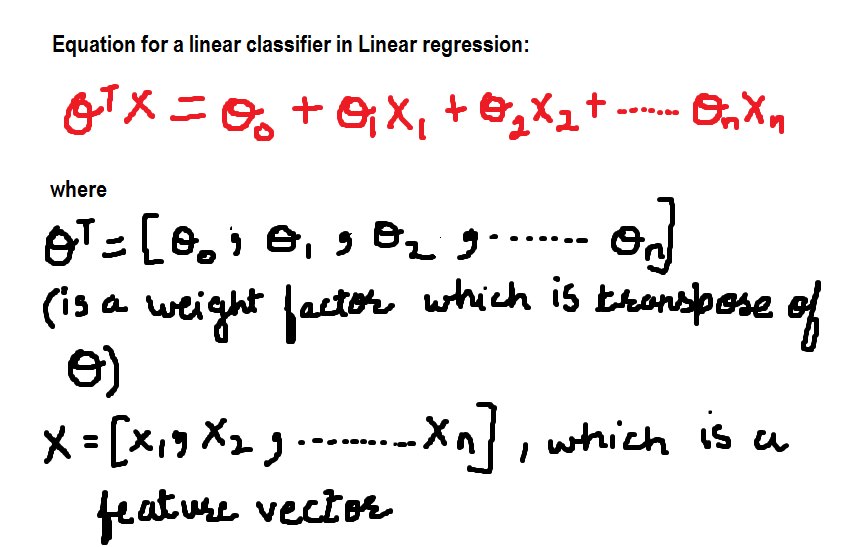
Por agora, A equação para o classificador linear é:
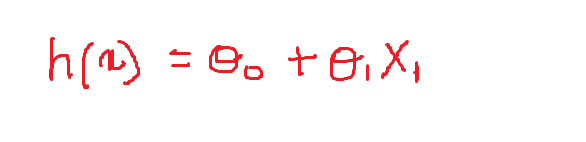
Agora vamos definir os valores dos pesos variáveis:
theta_0 = -1 e theta = 0.1
Então, nossa equação se parece com isso e o seguinte é o gráfico representando a equação no plano 2D:
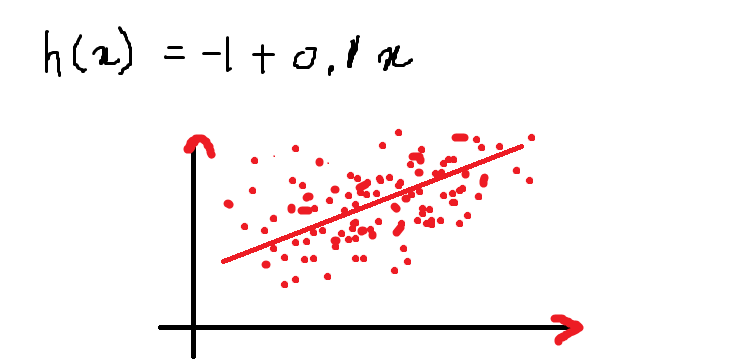
Acima está uma equação de uma linha para a equação dada:
h (x) = – 1 + 0.1x
O valor da função h (x) quando x = 13 isto é:
h (13) = – 1+ (0,1) * (13) = 0,3
Como descrito anteriormente neste artigo, Estou definindo o limiar em 0.5, que é qualquer valor de h maior do que (igual a) 0.5 será rotulado como 1 e, pelo contrário, 0. Podemos defini-lo da seguinte forma de função de etapa:

Agora, Conformemente, h tem um valor de 0.3, daí o valor da y_hat = 0 de acordo com a função definida acima.
Agora, Uma coisa deve notar aqui que cada valor maior do que 0.5, Suponha que eu diga que o valor de 'h’ isto é 1000 por algum valor de x, será então rotulado como 1 só, Não há diferença entre o valor 1 e 1000 uma vez que ambos são classificados como 1 só. Está correto? Podemos aceitar essa solução? Bem, não! Eu não aceitaria! !!!
Mais uma coisa, Qual é a probabilidade de que H tem um valor de 0.3? Todas essas perguntas permanecem sem resposta. Por essas razões, Os cientistas de dados não preferem usar regressão linear para fins de classificação.
Antes de continuar, Quero mostrar como a função se comporta graficamente y_hat:
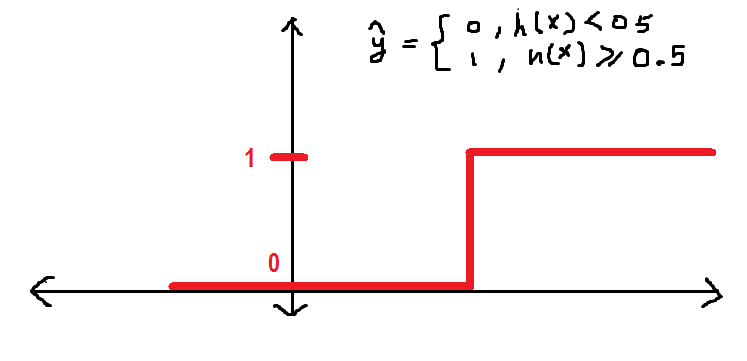
Será melhor se tivermos uma curva mais suave em vez da anterior. Vamos a ver:
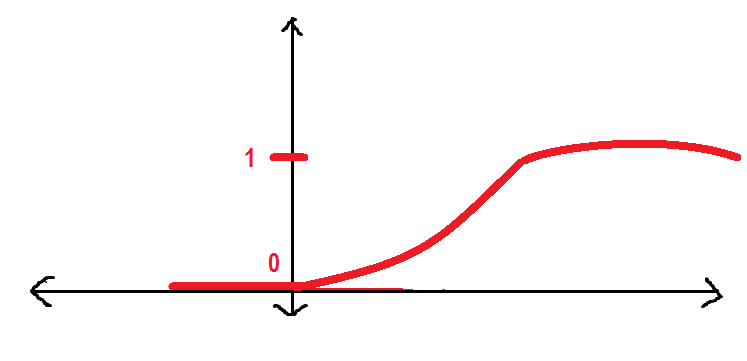
A curva anterior é conhecida como Função sigmoide que vamos usar ao longo deste artigo. Aqui eu vou introduzir a função sigmoid.
Qual é a função sigmoide?
A função sigmoide é representada pelo símbolo sigma. Su comportamiento gráfico se ha descrito en la figura"Figura" é um termo usado em vários contextos, Da arte à anatomia. No campo artístico, refere-se à representação de formas humanas ou animais em esculturas e pinturas. Em anatomia, designa a forma e a estrutura do corpo. O que mais, em matemática, "figura" está relacionado a formas geométricas. Sua versatilidade o torna um conceito fundamental em várias disciplinas.... anterior. A equação matemática para a função sigmoide é descrita abaixo:
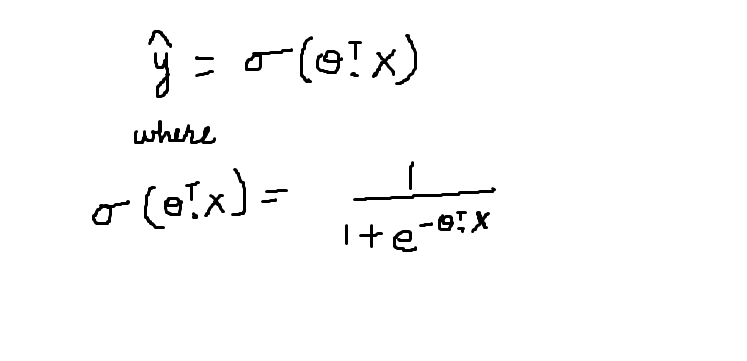
A função sigmoid dá a probabilidade de que os dados pertencem a uma classe específica que está no intervalo [0,1]. Aceita o produto escalar da transposição de e o vetor X característico como parâmetro. O valor resultante é a probabilidade.
Portanto, quando P (Y = 1 | X) = sigmóide (theta * X)
P (Y = 0 | X) = 1- Sigmóide (theta * X)
O que mais, Eu quero que você observe o comportamento da função sigmoid:
- Quando theta (transposição) * X fica muito maior, O valor do sigmoide torna-se igual a 1
- Quando theta (transposição) * X torna-se muito pequeno o valor do sigmoide torna-se igual a 0
Aplicações de regressão logística
Nesta secção, Gostaria de discutir algumas das aplicações da regressão logística.
1. Prever a probabilidade de uma pessoa ter um ataque cardíaco
2. Prever a propensão de um cliente a comprar um produto ou suspender uma assinatura.
3. Prever a probabilidade de falha de um determinado processo ou produto.
Antes de terminar este artigo, Eu só quero recapitular quando você deve usar a regressão logística:
- Quando seus dados são binários: 0/1, Verdade / Falso, sim / Não
- Quando você precisa de resultados probabilísticos
- Quando seus dados podem ser separados linearmente
- Quando você precisa entender o impacto do recurso.
Muitos outros algoritmos de classificação são amplamente utilizados além da regressão logística como kNN, Árvores de decisão, Algoritmos aleatórios de floresta e clustering como clustering K-means. Mas a regressão logística é um algoritmo amplamente utilizado e também fácil de implementar..
Então foi o algoritmo de regressão logística para iniciantes.. Nós falamos sobre tudo o que você precisa saber sobre a teoria da regressão logística. Espero que tenham gostado do meu artigo!!
A mídia mostrada neste artigo não é propriedade da DataPeaker e é usada a critério do autor.