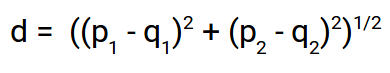Semelhança de imagem | Implementar similaridade de imagem em Python

Se você acha que nossa imagem de teste é semelhante à nossa primeira imagem de referência, é certo. Se você acredita de outra forma, Vamos descobrir junto com o poder da matemática e da programação.

“O futuro da pesquisa se concentrará em imagens em vez de palavras-chave”. – Ben Silbermann, CEO do Pinterest.

Imagem vetorial

Cada imagem é armazenada em nosso computador na forma de números e um vetor de tais números que pode descrever completamente nossa imagem é conhecido como Vetor de Imagem.

Distância euclidiana:

A distância euclidiana representa a distância entre quaisquer dois pontos em um espaço n-dimensional. Uma vez que representamos nossas imagens como vetores de imagens, eles nada mais são do que um ponto em um espaço de n dimensões e vamos usar a distância euclidiana para encontrar a distância entre eles.

Histograma:

Um histograma é uma exibição gráfica de valores numéricos. Usaremos o vetor imagem para as três imagens e então encontraremos a distância euclidiana entre elas.. Com base nos valores retornados, a imagem com uma distância menor é mais parecida que a outra.

Para encontrar a semelhança entre as duas imagens, vamos usar a seguinte abordagem:

1. Leia os arquivos de imagem como um array.
2. Como os arquivos de imagem são coloridos, existem 3 canais para valores RGB. Vamos nivelá-los para que cada imagem seja uma única matriz 1-D.
3. Assim que tivermos nossos arquivos de imagem como um array, vamos gerar um histograma para cada imagem onde para cada índice 0-255 vamos contar a ocorrência desse valor de pixel na imagem.
4. Assim que tivermos nossos histogramas, usaremos a regra L2 ou a distância euclidiana para encontrar a diferença entre os dois histogramas.
5. Com base na distância entre o histograma da nossa imagem de teste e as imagens de referência, podemos encontrar a imagem à qual nossa imagem de teste é mais semelhante..

Codificação para similaridade de imagem em Python

Importe as dependências que vamos usar

from PIL import Image
from collections import Counter
import numpy as np

Usaremos o NumPy para salvar a imagem como uma matriz NumPy, Imagem para ler a imagem em termos de valores numéricos e Contador para contar o número de vezes que cada valor de pixel ocorre (0-255) nas imagens.

Leia a imagem

reference_image_1 = Imagem.open('Reference_image1.jpg')
reference_image_arr = np.asarray(reference_image_1)
imprimir(np.shape(reference_image_arr))
>>> (250, 320, 3)

Podemos ver que nossa imagem foi lida corretamente como uma matriz 3-D. Na próxima etapa, devemos achatar esta matriz 3-D em uma matriz unidimensional.

flat_array_1 = array1.flatten()
imprimir(np.shape(flat_array_1))
>>> (245760, )

Faremos as mesmas etapas para as outras duas imagens. Vou pular aqui para que você possa testar mais a fundo.

Gerando o vetor de histograma de contagem:

RH1 = Contador(flat_array_1)

A próxima linha de código retorna um dicionário onde a chave corresponde ao valor do pixel e o valor chave é o número de vezes que o pixel está presente na imagem.

Uma limitação da distância euclidiana é que ela precisa que todos os vetores sejam normalizados, Em outras palavras, ambos os vetores devem ter as mesmas dimensões. Para ter certeza de que nosso vetor de histograma está normalizado, vamos usar um loop para de 0-255 e iremos gerar nosso histograma com o valor-chave se a chave estiver presente na imagem; caso contrário, nós adicionamos um 0.

H1 = []
para eu no alcance(256):
    se eu estiver em RH1.keys():
        H1.append(D1[eu])
    outro:
        H1.append(0)

O trecho de código acima gera um vetor de tamanho (256,) donde cada índiceo "Índice" É uma ferramenta fundamental em livros e documentos, que permite localizar rapidamente as informações desejadas. Geralmente, é apresentado no início de um trabalho e organiza os conteúdos de forma hierárquica, incluindo capítulos e seções. Sua correta preparação facilita a navegação e melhora a compreensão do material, tornando-se um recurso essencial para estudantes e profissionais de várias áreas.... corresponde al valor del píxel y el valor corresponde al recuento del píxel en esa imagen.

Seguimos os mesmos passos para as outras duas imagens e obtemos seus vetores de contagem-histograma correspondentes. Neste ponto, temos nossos vetores finais tanto para as imagens de referência quanto para a imagem de teste e tudo o que faremos é calcular as distâncias e prever.

Função de distância euclidiana:

def L2Norm(H1,H2):
    distance =0
    for i in range(len(H1)):
        distância + = np.square(H1[eu]-H2[eu])
    return np.sqrt(distância)

La función anterior toma dos histogramasHistogramas são representações gráficas que mostram a distribuição de um conjunto de dados. Eles são construídos dividindo o intervalo de valores em intervalos, o "Caixas", e contando quantos dados caem em cada intervalo. Essa visualização permite identificar padrões, tendências e variabilidade de dados de forma eficaz, facilitando a análise estatística e a tomada de decisões informadas em várias disciplinas.... y devuelve la distancia euclidiana entre ellos.

Avaliação:

Como temos tudo o que precisamos para encontrar as semelhanças na imagem, Vamos descobrir a distância entre a imagem de teste e nossa primeira imagem de referência.

dist_test_ref_1 = L2Norm(H1, test_H)
imprimir("A distância entre Reference_Image_1 e Test Image é : {}".formato(dist_test_ref_1))
>>> A distância entre Reference_Image_1 e Test Image é : 9882.175468994668

Vamos agora descobrir a distância entre a imagem de teste e nossa segunda imagem de referência.

dist_test_ref_2 = L2Norm(H2, test_H)
imprimir("A distância entre Reference_Image_2 e Test Image é : {}".formato(dist_test_ref_2))
>>> A distância entre Reference_Image_2 e Test Image é : 137929.0223122023

conclusão

Com base em resultados anteriores, podemos ver que a distância entre nossa imagem de teste e nossa primeira imagem de referência é muito menor do que a distância entre nosso teste e nossa segunda imagem de referência, o que faz sentido porque tanto a imagem de teste quanto nossa primeira imagem de referência são imagens de Piegon, enquanto nossa segunda imagem de referência é de um pavão.

No próximo tutorial, aprendemos como usar matemática básica e pouca programação para construir nosso próprio preditor de semelhança de imagens com resultados bastante decentes.

O código completo pode ser encontrado junto com as imagens. aqui.

Sobre o autor

Meu nome é Prateek Agrawal e sou um estudante do terceiro ano no Instituto Indiano de Design e Fabricação de Tecnologia da Informação Kancheepuram, cursando B.Tech e M.Tech Dual Degree em Ciência da Computação. Sempre tive um talento especial para aprendizado de máquina e ciência de dados e tenho praticado isso há cerca de um ano e tenho algumas vitórias em meu currículo..

Eu pessoalmente acredito que Paixão é tudo que você precisa. Lembro-me de ficar com medo de ouvir as pessoas falarem sobre a CNNS, RNN e Deep Learning porque eu não conseguia entender uma única parte, mas eu não desisti. Eu tive a paixão e comecei a dar pequenos passos em direção ao aprendizado e aqui estou postando meu primeiro blog. Espero que você tenha gostado de ler isso e se sinta um pouco autoconfiante. Confie em mim, sim posso, você pode.

Por favor, escreva-me em caso de dúvidas ou apenas para dizer olá.

LinkedIn: https://www.linkedin.com/in/prateekagrawal1405/
Github: https://github.com/prateekagrawaliiit

Créditos

• Wikipedia
• AnalyticsAnalytics refere-se ao processo de coleta, Meça e analise dados para obter insights valiosos que facilitam a tomada de decisões. Em vários campos, como negócio, Saúde e esporte, A análise pode identificar padrões e tendências, Otimize processos e melhore resultados. O uso de ferramentas avançadas e técnicas estatísticas é essencial para transformar dados em conhecimento aplicável e estratégico.... Vidhya
• Metade
• Imagens do google