Este artigo foi publicado como parte do Data Science Blogathon.
Introdução
Este trabalho tem como objetivo apresentar a simulação de Monte Carlo para análise de incertezas variávelEm estatística e matemática, uma "variável" é um símbolo que representa um valor que pode mudar ou variar. Existem diferentes tipos de variáveis, e qualitativo, que descrevem características não numéricas, e quantitativo, representando quantidades numéricas. Variáveis são fundamentais em experimentos e estudos, uma vez que permitem a análise de relações e padrões entre diferentes elementos, facilitando a compreensão de fenômenos complexos..... Monte Carlo pode substituir a propagação de erro porque supera as desvantagens da propagação de erro. Discutiremos:
- Como propagar o erro;
- Por que usar Monte Carlo em vez de propagação de erro? e
- Os passos para perceber a incerteza de Monte Carlo.
Vamos começar esta discussão com coisas simples. Quanto um funcionário da cidade A gasta em despesas de manutenção por mês? Existem milhares de funcionários na cidade A com diferentes despesas de subsistência. Para responder a pergunta anterior, devemos perguntar a vários funcionários e registrar suas respostas. Esses funcionários vão responder de forma diferente. Seu custo de vida irá variar em uma distribuição de probabilidade. Embora não tenhamos recursos para solicitar a todos os funcionários, podemos experimentar um grupo de, por exemplo, 50 funcionários para que a pesquisa represente a população.
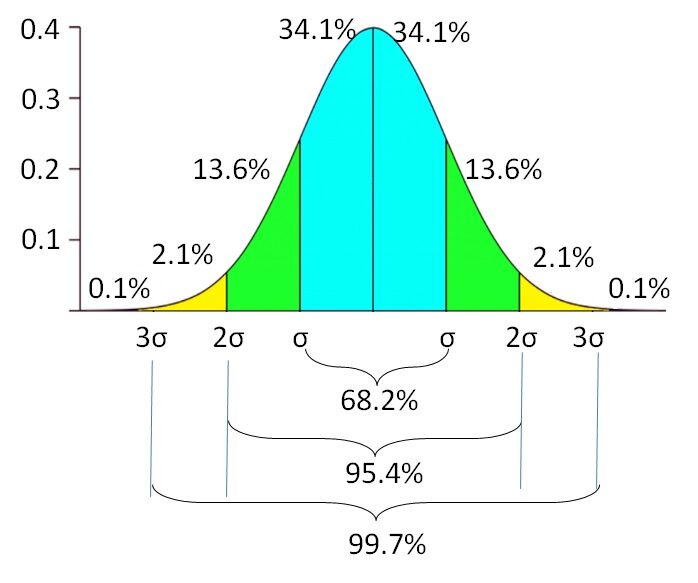
Porém, ainda precisamos de um número para representar o custo total de vida. Digamos que entendemos que a despesa média mensal de vida é $ 2000. O bem, Outra maneira é usar o medianaA mediana é uma medida estatística que representa o valor central de um conjunto de dados ordenados. Para calculá-lo, Os dados são organizados do menor para o maior e o número no meio é identificado. Se houver um número par de observações, Os dois valores principais são calculados em média. Este indicador é especialmente útil em distribuições assimétricas, uma vez que não é afetado por valores extremos.... para representar o gasto total. Para expressar outras possíveis despesas de subsistência, podemos usar o desvio padrão. Por exemplo, gasto mensal de vida na cidade A é $ 2000 ± 500 (média ± desvio padrão).
Isso significa que se os dados são normalmente distribuídos, a 68,2% de funcionários gastam entre $ 1500 e $ 2500. Há outro 31,8% de funcionários que gastam menos do que $ 1500 e mais de $ 2500 no custo de vida mensal. A probabilidade de o gasto de vida diminui para mediro "medir" É um conceito fundamental em várias disciplinas, que se refere ao processo de quantificação de características ou magnitudes de objetos, Fenômenos ou situações. Na matemática, Usado para determinar comprimentos, Áreas e volumes, enquanto nas ciências sociais pode se referir à avaliação de variáveis qualitativas e quantitativas. A precisão da medição é crucial para obter resultados confiáveis e válidos em qualquer pesquisa ou aplicação prática.... que está longe da média. Existe uma probabilidade de 0,1% de encontrar funcionários com despesas de subsistência menores que $ 500 o superiores a $ 3500. O desvio padrão reflete a incerteza variável das despesas de vida. Indica a extensão inferior e superior da variável, em vez de confiar em um único valor.
Propagação de erro
Como os funcionários da cidade A têm renda: $ 3200 ± 2000, custo de vida: $ 2000 ± 500, crédito: $ 180 ± 130, receitas ou despesas inesperadas: $ 20 ± 300 e taxa de juros do banco: 0,85 ± 0,35% por mês. Queremos calcular quanto um funcionário pode economizar em um mês. A equação é expressa abaixo:
Poupança = (Renda – Custo de vida – Crédito + Renda / despesas inesperadas) × (1 + Interesses)
A economia mensal é calculada como a renda total deduzida das despesas de moradia e crédito e adicionada a receitas ou despesas inesperadas.. Depois de um mês, a poupança nominal aumenta devido aos juros bancários. Vamos calcular a economia média mensal e a incerteza. Veja a seguinte equação sobre como calcular a incerteza.
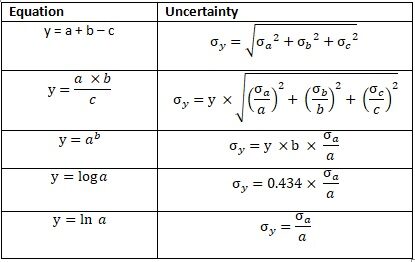
Fig. 2 Propagação de erro
Salvando 1 = ((3200 ± 2000) - (2000 ± 500) - (180 ± 130) + (20 ± 300)) × (1 + (0.0085 ± 0.0035)) Salvando 1 = 1040 ± σSaving_1
σSaving_1 = ((20002 + 5002 + 1302 + 20002))0.5 σSaving_1 = 2087
Salvando 1 ± σSaving_1 = 1040 ± 2087
Isso calcula a economia mensal após contabilizar os juros bancários.
Salvando = Salvando 1 × (1 + (0.0085 ± 0.0035)) Salvando = (1040 ± 2087) × (1.0085 ± 0.0035) Salvando = 1049 ± σSaving_2
σSalvando = 1049 × ((2087/1040)2 + (0.0035/1.0085)2)0.5 σSalvando = 1049 × 2.01 σSalvando = 2105
Poupança ± σSalvando = 1049 ± 2105
Do resultado, nós podemos ver isso, em média, as pessoas podem salvar $ 1049 em um mês com a incerteza de $ 2105. O limite inferior da economia mensal é – $ 1056 ($ 1049 – $ 2105), o que é um valor negativo. A própria incerteza é 2105, o que é 2 vezes maior que o valor médio. Se visualizarmos o gráfico, podemos ver que as economias dos funcionários variam de – $ 6000 e $ 8000. Parece estranho porque os limites inferior e superior são quase equilibrados. Creio que, na realidade, o valor da economia deve ter uma variabilidade maior do que o valor do déficit.
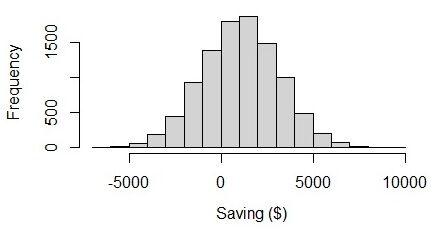
Fig. 3 Visualização da economia em uma distribuição normal
Como isso esta acontecendo? O problema está nos dados de renda. A renda de $ 3200 ± 2000 tem alta incerteza devido à variabilidade da receita. A incerteza é mais de um terço do valor médio. Se assumirmos que esta é uma distribuição normal, veremos que o 4.8% da população tem rendimentos abaixo 0, o que não parece provável que aconteça. De fato, a renda deve estar sempre acima de% 0. Este problema ocorre quando assumimos que todas as variáveis são normalmente distribuídas, mas na realidade eles não são.
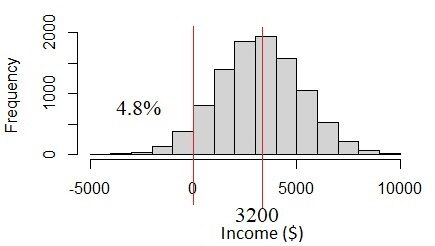
Fig. 4 Distribuição normal se o desvio padrão da renda for muito grande
Simulação de Monte Carlo
Qual é a solução? Outra forma de avaliar a incerteza é aplicando a simulação de Monte Carlo. Monte Carlo é originalmente o nome de uma área administrativa em Mônaco. Mas o Monte Carlo em nossa discussão hoje é coisa estatística.. Monte Carlo pode superar o lado negativo da propagação do erro. A simulação de Monte Carlo, em oposição à propagação do erro, pode trabalhar em uma distribuição de dados diferente da distribuição normal e em dados com um grande desvio padrão.

Fig. 5 Monte Carlo em Mônaco. Fonte: Mapa de Google
A simulação de Monte Carlo simula ou gera um conjunto de números aleatórios de acordo com a distribuição dos dados e a parametroso "parametros" são variáveis ou critérios usados para definir, medir ou avaliar um fenômeno ou sistema. Em vários domínios, como a estatística, Ciência da Computação e Pesquisa Científica, Os parâmetros são essenciais para estabelecer normas e padrões que orientam a análise e interpretação dos dados. Sua seleção e manuseio adequados são cruciais para obter resultados precisos e relevantes em qualquer estudo ou projeto.... de cada variável. Uma vez gerado, todos os valores das variáveis são calculados usando a equação. Isso parece um pouco mais complicado do que usar propagação de erro. Mas use ferramentas de ciência de dados, como Python o R, vai ser muito simples. Nesta discussão, vamos demonstrar o uso da linguagem estatística R.
Etapas para realizar uma simulação de Monte Carlo
1. Verifique a função de densidade de probabilidade da distribuição de dados.
Digamos que examinemos o registro de dados fornecido pela pesquisa de 50 pesquisado. Existem muitos tipos de funções de densidade de probabilidade e temos que determinar qual se encaixa em nossos dados. Variáveis com distribuição normal são apenas despesas de subsistência e receitas ou despesas inesperadas. A distribuição dos dados de renda é positiva.
Neste caso, vamos tratá-lo como uma distribuição gama. É por isso que a média e a propagação do erro não são adequadas para esses dados.. As outras duas variáveis também não têm distribuição normal.. A taxa de juros do banco é distribuída uniformemente entre 0,3 e 1,5.
A distribuição de dados sobre empréstimos para saldar crédito é bastante peculiar. Os dados são distribuídos principalmente em dois grupos populacionais. O primeiro grupo tem menos crédito do que o segundo. Digamos que a distribuição de dados de crédito não se encaixe em nenhuma função de densidade de probabilidade. Mais tarde, vamos usar uma distribuição não paramétrica.
2. Gerar simulação Monte Carlo
Gerar simulação de Monte Carlo significa gerar um conjunto de números aleatórios com a mesma distribuição de dados que os dados originais. Para fazer isso, simplesmente definimos o número de simulações e os parâmetros de distribuição de acordo com o tipo de distribuição. Definimos o número de simulações para 10,000. Isso significa que vamos simular os dados de 50 pesquisado em 10,000 dados.
Os parâmetros da distribuição normal são médios / média e desvio padrão. Sabemos que as médias ± desvios padrão das despesas de subsistência e receitas ou resultados inesperados são 2000 ± 500 e 20 ± 300 respectivamente. Agora, podemos gerar as distribuições. Neste artigo, Vou usar a linguagem R. Claro, outras linguagens de ciência de dados, como Python, eles podem fazer isso também. Veja que os dados simulados têm uma média e um padrão semelhantes, não é o mesmo, do que parâmetros de entrada.
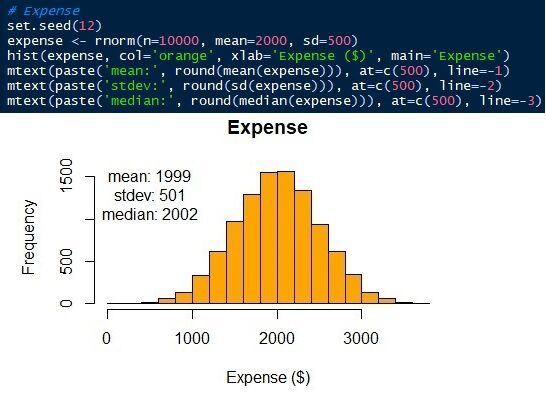
Fig. 6 Distribuição normal de despesas de subsistência
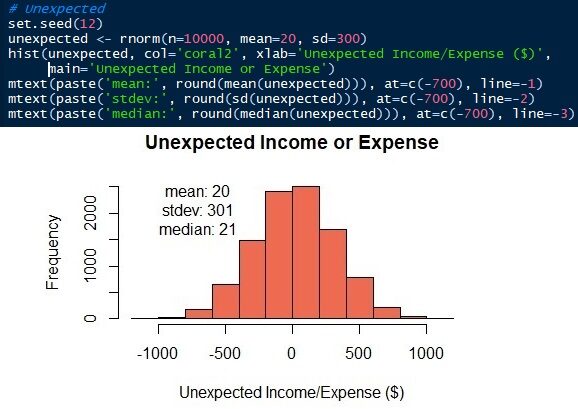
Fig. 7 Distribuição normal de receitas ou despesas inesperadas
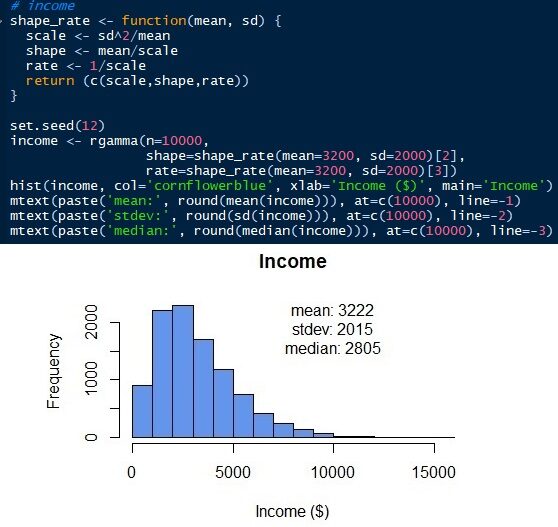
Para gerar a distribuição gama, precisamos conhecer outros parâmetros. Ao contrário da distribuição normal, a distribuição gama tem escala, forma e velocidade como parâmetros. Mas podemos obter esses parâmetros com a média e o desvio padrão (a partir de). Scale = sd2/significar. Forma = médio / escala. Taxa = 1 / escala. Mais tarde, podemos simular a distribuição gama da renda dos funcionários, conforme mostrado abaixo. A distribuição gama só pode ter valores positivos. Não há nenhum valor abaixo 0 uma vez que a renda de todos os funcionários deve ser um número positivo. A distribuição normal daria valores negativos se o erro padrão for muito grande. Veja que a distribuição simulada tem uma média e desvio padrão de 3222 e 2015 respectivamente, que estão próximos dos parâmetros de entrada originais. Mas temos uma mediana de 2805. A mediana da distribuição gama, ao contrário da distribuição normal, está longe da média.
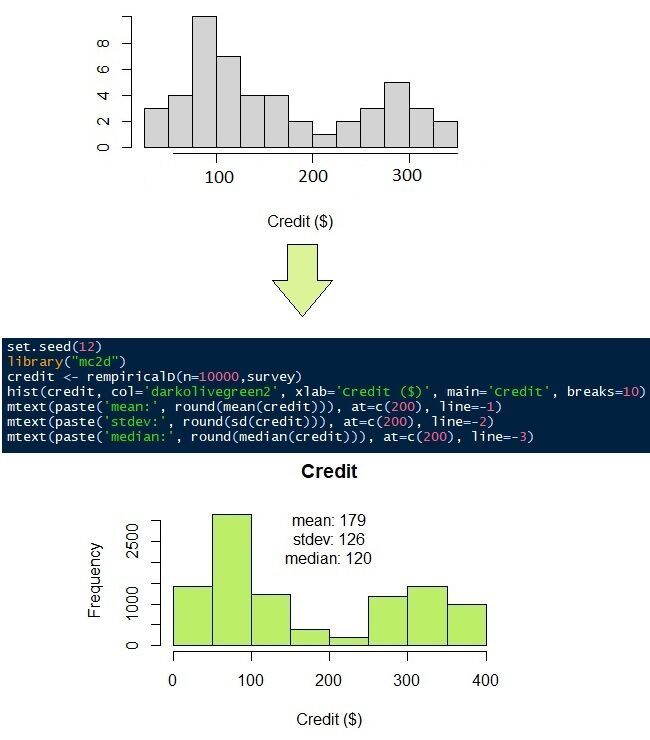
O crédito para pagar mensalmente, como mencionado anteriormente, não tem uma função de densidade de probabilidade adequada. Dê uma olhada nas respostas de 50 Pesquisas no Figura"Figura" é um termo usado em vários contextos, Da arte à anatomia. No campo artístico, refere-se à representação de formas humanas ou animais em esculturas e pinturas. Em anatomia, designa a forma e a estrutura do corpo. O que mais, em matemática, "figura" está relacionado a formas geométricas. Sua versatilidade o torna um conceito fundamental em várias disciplinas.... 9 (histograma cinza). Parece que a maioria das pessoas tem que pagar seu crédito de $ 100 e $ 300. Para simular o 50 observações em 10,000 observações, podemos usar uma distribuição não paramétrica. Como o próprio nome sugere, distribuição não paramétrica não requer parâmetros, como média, o desvio padrão, a forma ou a taxa, assim como as distribuições normal e gama. Requer apenas os dados originais.
A última variável a simular é a taxa de juros do banco. A taxa de juros do banco varia de 0,3 uma 1,5 uniformemente. Vamos fazer o mesmo 10,000 observações que variam de 0.3 uma 1.5 com a mesma probabilidade.
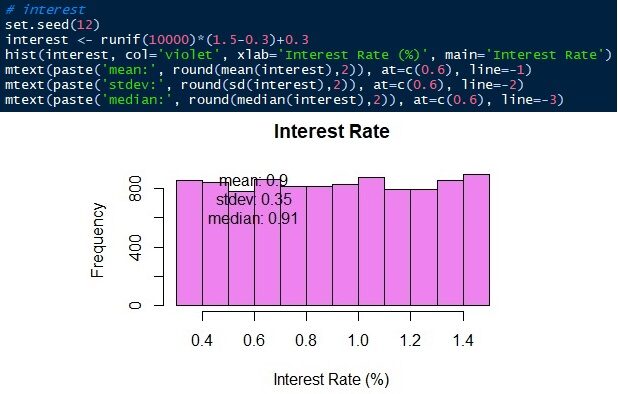
3. Combinação de simulações de Monte Carlo
A última etapa é combinar as Simulações de Monte Carlo usando a equação para calcular a economia mensal. Para fazer isso, só precisamos colocar todas as simulações juntas em uma mesa. Mais tarde, podemos calcular 10,000 linhas de economia mensal. O resultado é $ 1073 ± 2052, não muito diferente da propagação do erro. Mas, Simulação de Monte Carlo mostra densidade de probabilidade. Podemos ver que a economia média é $ 666 e os dados variam de $ 2000 e 10000.

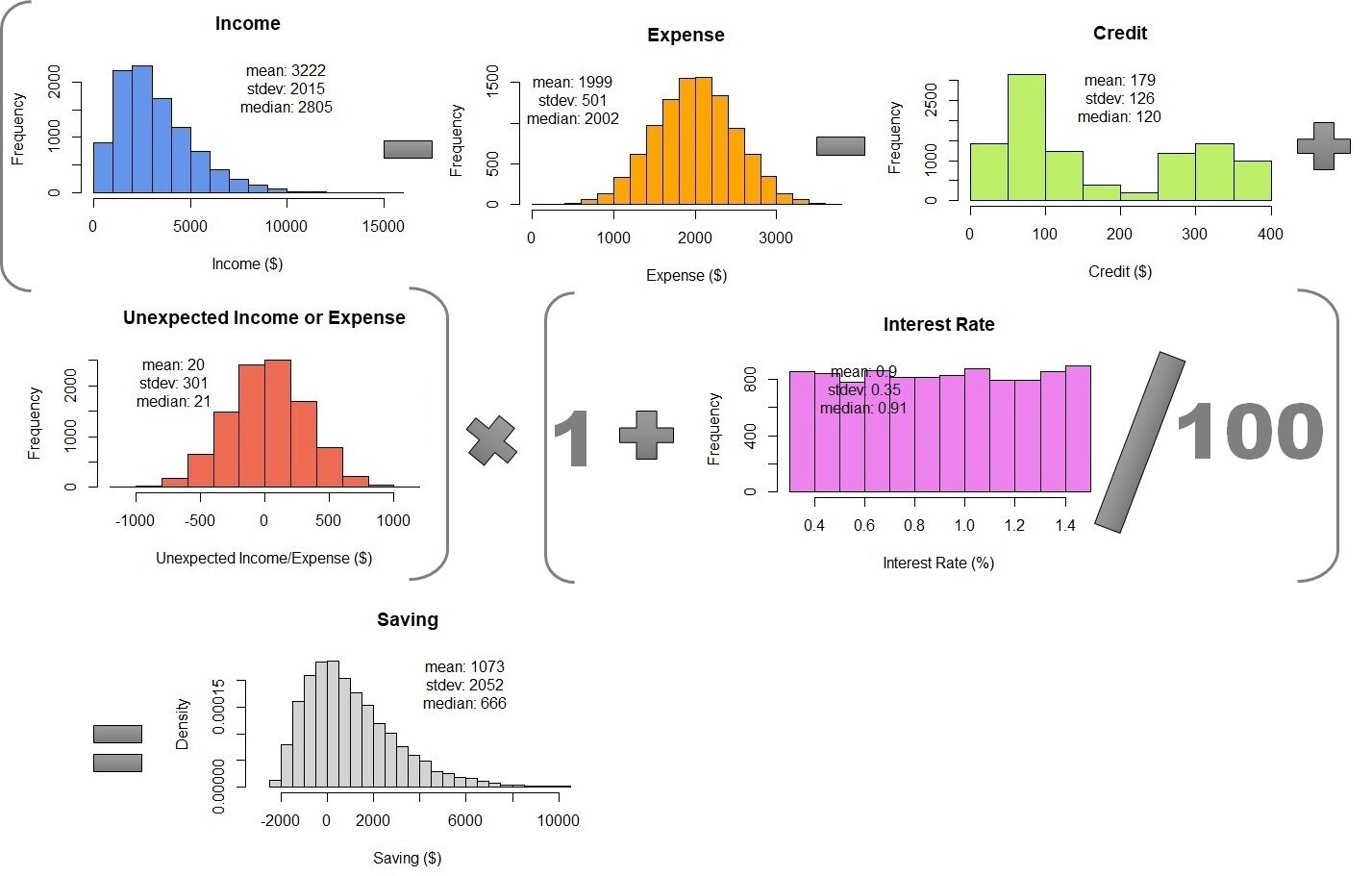
Tabela 1 – Combinação de simulações de Monte Carlo
Agora, vamos olhar para outro exemplo com variabilidade espacial e temporal. A tarefa é calcular o escoamento superficial de uma bacia. A bacia é o limite da hidrologia das águas superficiais. Toda a chuva que cai abaixo da bacia não ultrapassará o limite. Parte da chuva infiltra-se no solo de acordo com o tamanho das partículas do solo e o tipo de cobertura do solo. A água que não se infiltra no solo é chamada de escoamento superficial. O escoamento superficial fluirá para o rio como descarga do rio.
A tabela a seguir mostra a intensidade da precipitação mensal em um ano e o coeficiente de escoamento em um 1,5 km.2 cuenca. A incerteza pode ser devido à heterogeneidade espacial e temporal. O coeficiente de precipitação e escoamento (devido ao tipo de solo e cobertura da terra) varia espacialmente na bacia. A precipitação da bacia é medida com vários pluviômetros. Eles fornecem precipitação média com incerteza devido à distribuição espacial. A distribuição da cobertura do solo também dá a incerteza do coeficiente de escoamento.
Um coeficiente de escoamento é a proporção da chuva que não infiltra no solo e se torna escoamento superficial. A floresta ou tipo de solo espesso tem um baixo coeficiente de escoamento. Assentamentos ou casas têm um alto coeficiente de escoamento. A conversão da cobertura florestal em assentamentos aumenta o coeficiente de escoamento porque uma proporção maior da água da chuva será escoamento superficial.
A variabilidade temporal também ocorre porque as chuvas nas estações chuvosa e seca são diferentes.. A mudança na cobertura do solo ao longo do tempo também causa a variabilidade temporal do coeficiente de escoamento. Outras fontes de incerteza são a qualidade das ferramentas de medição, métodos de medição, condições ambientais e outras condições inexplicáveis devido à falta de conhecimento.
| Meu | Precipitação (milímetros / minha) | Coeficiente de escoamento | Área (km2) |
| 1 | 320 ± 37 | 0,3 ± 0,2 | 1,5 |
| fevereiro | 350 ± 59 | 0,3 ± 0,2 | 1,5 |
| março | 205 ± 26 | 0,4 ± 0,1 | 1,5 |
| Abr | 170 ± 41 | 0,4 ± 0,1 | 1,5 |
| maionese | 106 ± 48 | 0,4 ± 0,1 | 1,5 |
| junho | 91 ± 32 | 0,4 ± 0,1 | 1,5 |
| jul | 77 ± 16 | 0,4 ± 0,1 | 1,5 |
| atrás | 52 ± 15 | 0,7 ± 0,2 | 1,5 |
| set | 100 ± 50 | 0,7 ± 0,2 | 1,5 |
| outubro | 120 ± 46 | 0,7 ± 0,2 | 1,5 |
| nov | 253 ± 45 | 0,7 ± 0,2 | 1,5 |
| Dez | 210 ± 48 | 0,7 ± 0,2 | 1,5 |
A equação é escoamento superficial = intensidade da chuva × coeficiente de escoamento × área da bacia. Toda a distribuição é simulada usando uma distribuição gama. O escoamento superficial médio mensal é 124.000 ± 30 m3/minha. A mediana é 120.000 m3/minha.
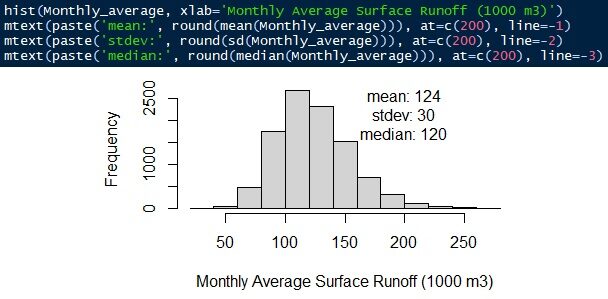
Fig. 12 Escoamento superficial médio mensal
Sobre o autor
Conecte-se comigo aqui https://www.linkedin.com/in/rendy-kurnia/
A mídia mostrada neste artigo não é propriedade da DataPeaker e é usada a critério do autor.






