Este artigo foi publicado como parte do Data Science Blogathon.
Visão geral
O cluster K-means é um algoritmo de aprendizado de máquina não supervisionado muito famoso e poderoso. Usado para resolver muitos problemas complexos de aprendizado de máquina não supervisionado. Antes de começar, Vamos dar uma olhada nos pontos que vamos entender.
Tabela de conteúdo
- Introdução
- Como funciona o algoritmo K-means?
- Como escolher o valor de K?
- Método do cotovelo.
- Método Silhouette.
- Vantagens do k-means.
- Desvantagens do k-means.
Introdução
Vamos entender o algoritmo de agrupamentoo "agrupamento" É um conceito que se refere à organização de elementos ou indivíduos em grupos com características ou objetivos comuns. Este processo é usado em várias disciplinas, incluindo psicologia, Educação e biologia, para facilitar a análise e compreensão de comportamentos ou fenômenos. No campo educacional, por exemplo, O agrupamento pode melhorar a interação e o aprendizado entre os alunos, incentivando o trabalho.. de K-means com sua definição simples.
Um algoritmo de agrupamento K-means tenta agrupar itens semelhantes na forma de clusters. O número de grupos é representado por K.
Vamos dar um exemplo. Suponha que você foi a uma loja de vegetais para comprar alguns vegetais. Lá você verá diferentes tipos de vegetais. A única coisa que você notará é que os vegetais serão organizados em um grupo de seus tipos. Como todas as cenouras ficarão no mesmo lugar, batatas vão ficar com seus tipos e assim por diante. Se você notar aqui, então você descobrirá que eles estão formando um grupo ou grupo, onde cada um dos vegetais é mantido dentro de seu tipo de grupo, formando os grupos.
Agora vamos entender isso com a ajuda de uma bela figura"Figura" é um termo usado em vários contextos, Da arte à anatomia. No campo artístico, refere-se à representação de formas humanas ou animais em esculturas e pinturas. Em anatomia, designa a forma e a estrutura do corpo. O que mais, em matemática, "figura" está relacionado a formas geométricas. Sua versatilidade o torna um conceito fundamental em várias disciplinas.....
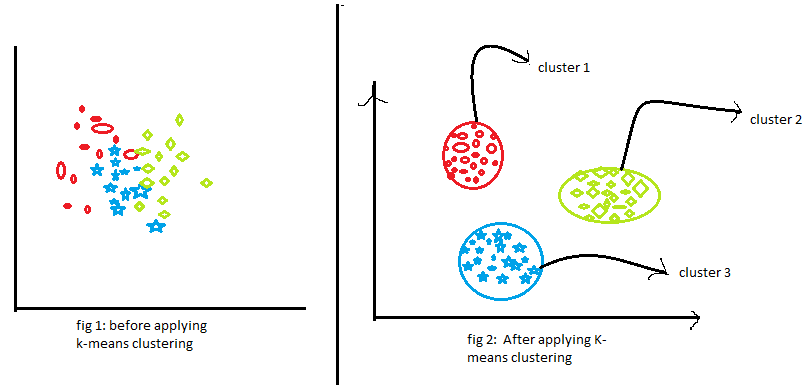
Agora, olhe para as duas figuras acima. O que você observou? Vamos falar sobre a primeira figura. A primeira figura mostra os dados antes de aplicar o algoritmo de agrupamento k-means. Aqui, as três categorias diferentes são confusas. Quando você vê esses dados no mundo real, você não será capaz de descobrir as diferentes categorias.
Agora, olhe para a segunda figura (figura 2). Isso mostra os dados após a aplicação do algoritmo de agrupamento K-means. você pode ver que os três itens diferentes são classificados em três categorias diferentes que são chamadas de grupos.
Como funciona o algoritmo de agrupamento K-means?
O agrupamento K-means tenta agrupar tipos semelhantes de itens na forma de agrupamentos. Encontre a semelhança entre os elementos e agrupe-os em grupos. O algoritmo de agrupamento K-means funciona em três etapas. Vamos ver quais são essas três etapas.
- Selecione os valores k.
- Inicialize os centróides.
- Selecione o grupo e encontre a média.
Vamos entender os passos acima com a ajuda da figura porque uma boa imagem é melhor do que milhares de palavras.
Vamos entender cada figura uma por uma.
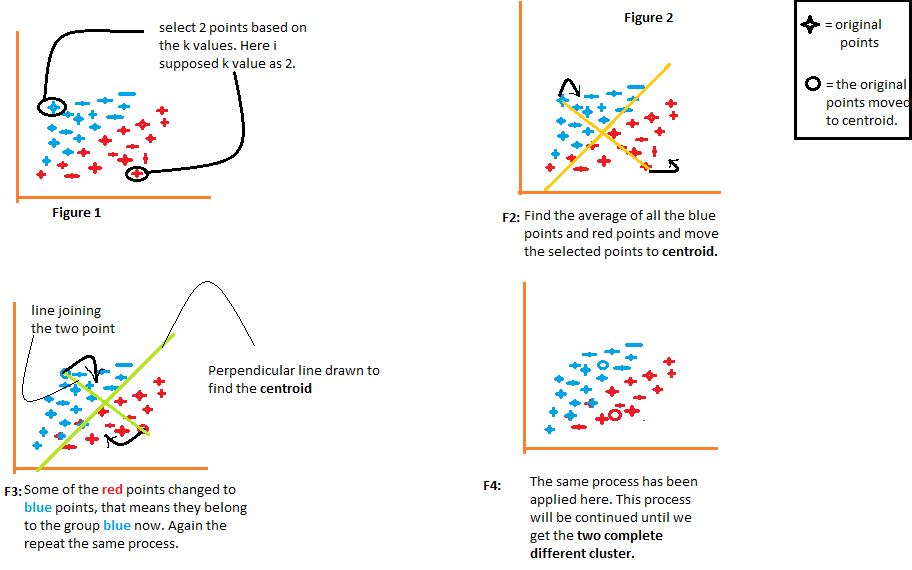
- A figura 1 mostra a representação de dados de dois elementos diferentes. o primeiro item é mostrado em azul e o segundo item é mostrado em vermelho. Aqui eu escolho o valor de K aleatoriamente como 2. Existem diferentes métodos pelos quais podemos escolher os valores de k corretos.
- Na figura 2, junte os dois pontos selecionados. Agora, para encontrar o centróide, vamos desenhar uma linha perpendicular a essa linha. Os pontos irão para o centroide. Se você olhar lá, você verá que alguns dos pontos vermelhos agora se movem para os pontos azuis. Agora, esses pontos pertencem ao grupo de elementos azuis.
- O mesmo processo continuará na figura 3. Vamos juntar os dois pontos e desenhar uma reta perpendicular a ela e encontrar o centróide. Agora os dois pontos se moverão para seu centroide e novamente alguns dos pontos vermelhos se transformarão em pontos azuis.
- O mesmo processo está acontecendo na figura 4. Este processo continuará até que tenhamos dois grupos completamente diferentes desses grupos.
NOTA: Observe que o agrupamento de K-médias usa o método da distância euclidiana para descobrir a distância entre os pontos.
Você encontrará muitas explicações sobre a distância euclidiana na Internet.
Como escolher o valor de K?
Uma das tarefas mais desafiadoras deste algoritmo de agrupamento é escolher os valores corretos de k. Qual deve ser o valor de k correto? Como escolher o valor k? Vamos encontrar a resposta para essas perguntas. Se você escolher os valores k aleatoriamente, pode ser certo ou errado. Se você escolher o valor errado, afetará diretamente o desempenho do seu modelo. Então, Existem dois métodos pelos quais você pode selecionar o valor correto de k.
- Método do cotovelo.
- Método Silhouette.
Agora, vamos entender os dois conceitos um por um em detalhes.
Método do cotovelo
O cotovelo é um dos métodos mais famosos pelo qual você pode selecionar o valor correto de k e aumentar o desempenho do seu modelo. Também realizamos ajuste de hiperparâmetros para escolher o melhor valor de k. Vamos ver como esse método de cotovelo funciona.
É um método empírico para encontrar o melhor valor de k. colete a gama de valores e tire o melhor deles. Calcule a soma do quadrado dos pontos e calcule a distância média.
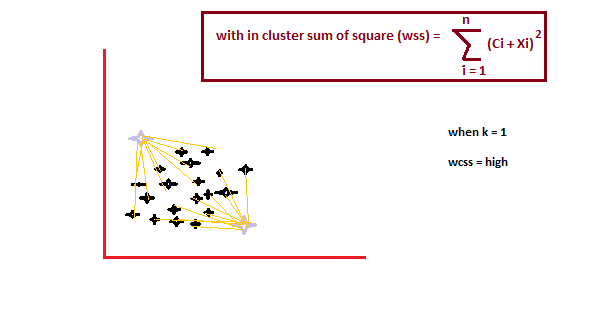
Quando o valor de k é 1, a soma do quadrado dentro do grupo será alta. UMA mediro "medir" É um conceito fundamental em várias disciplinas, que se refere ao processo de quantificação de características ou magnitudes de objetos, Fenômenos ou situações. Na matemática, Usado para determinar comprimentos, Áreas e volumes, enquanto nas ciências sociais pode se referir à avaliação de variáveis qualitativas e quantitativas. A precisão da medição é crucial para obter resultados confiáveis e válidos em qualquer pesquisa ou aplicação prática.... que aumenta o valor de k, a soma do valor quadrado dentro do grupo diminuirá.
Finalmente, vamos traçar um gráfico entre os valores k e a soma do quadrado dentro do grupo para obter o valor k. Vamos examinar o gráfico cuidadosamente. Algum dia, nosso gráfico diminuirá abruptamente. Esse ponto será considerado como um valor de k.
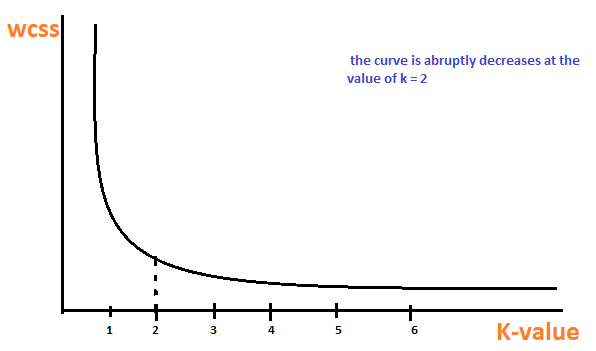
Método Silhouette
O método da silhueta é um pouco diferente. O método do cotovelo também leva o intervalo de valores k e desenha o gráfico de silhueta. Calcule o coeficiente de silhueta de cada ponto. Encontre a distância média de pontos dentro de seu grupo para (eu) e a distância média dos pontos para seu próximo grupo mais próximo chamado b (eu).

Observação: O A (eu) o valor deve ser menor que b (eu) valor, o que é ai << com um.
Agora, nós temos os valores de um (eu) e B (eu). vamos calcular o coeficiente de silhueta usando a seguinte fórmula.
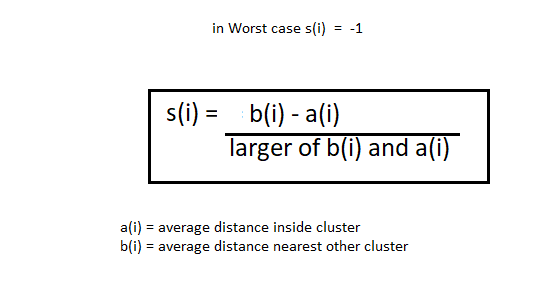
Agora, podemos calcular o coeficiente de silhueta de todos os pontos nos grupos e traçar o gráfico de silhueta. Este gráfico também será útil para detectar outliers. O enredo da silhueta está entre -1 uma 1.
Observe que para o coeficiente de silhueta igual a -1 é o pior caso.
Olhe para o gráfico e verifique qual dos valores k está mais próximo de 1.
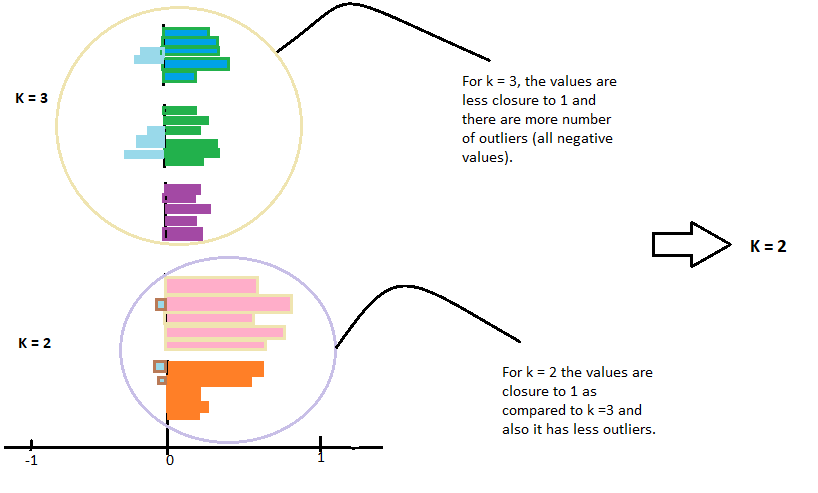
O que mais, verifique o gráfico que tem o mínimo de outliers, o que significa um valor menos negativo. Em seguida, escolha o valor de k para o seu modelo ajustá-lo.
Vantagens do K-means
- É muito fácil de implementar.
- É escalonável para um grande conjunto de dados e também mais rápido para grandes conjuntos de dados.
- adaptar novos exemplos com muita frequência.
- Generalização de clusters para diferentes formas e tamanhos.
Desvantagens do K-means
- É sensível a outliers.
- Escolher os valores k manualmente é um trabalho árduo.
- Conforme o número de dimensões aumenta, sua escalabilidade diminui.