Este artículo fue publicado como parte del Blogatón de ciencia de datos.
Introducción
se utiliza para predecir valores futuros basados en valores observados previamente y una de las mejores herramientas para el análisis de tendencias y la predicción futura.
¿Qué son los datos de series de tiempo?
Se registra a intervalos de tiempo regulares y el orden de estos puntos de datos es importante. Por tanto, cualquier modelo predictivo basado en datos de series de tiempo tendrá el tiempo como variableEn estadística y matemáticas, una "variable" es un símbolo que representa un valor que puede cambiar o variar. Existen diferentes tipos de variables, como las cualitativas, que describen características no numéricas, y las cuantitativas, que representan cantidades numéricas. Las variables son fundamentales en experimentos y estudios, ya que permiten analizar relaciones y patrones entre diferentes elementos, facilitando la comprensión de fenómenos complejos.... independiente. El resultado de un modelo sería el valor o la clasificación pronosticados en un momento específico.
Análisis de series de tiempo vs pronóstico de series de tiempo
Hablemos de alguna posible confusión sobre el análisis y la previsión de series de tiempo. El pronóstico de series de tiempo es un ejemplo de modelado predictivo, mientras que el análisis de series de tiempo es una forma de modelado descriptivo.
Para un nuevo inversor, la investigación general asociada con la bolsa o el mercado de acciones no es suficiente para tomar la decisión. La tendencia común hacia el mercado de valores entre la sociedad es altamente riesgosa para la inversión, por lo que la mayoría de las personas no pueden tomar decisiones basadas en tendencias comunes. La variación estacional y el flujo constante de cualquier índiceEl "Índice" es una herramienta fundamental en libros y documentos, que permite ubicar rápidamente la información deseada. Generalmente, se presenta al inicio de una obra y organiza los contenidos de manera jerárquica, incluyendo capítulos y secciones. Su correcta elaboración facilita la navegación y mejora la comprensión del material, convirtiéndolo en un recurso esencial tanto para estudiantes como para profesionales en diversas áreas.... ayudarán a los inversores nuevos y existentes a comprender y tomar la decisión de invertir en el mercado de valores.
Para resolver este tipo de problemas, el pronóstico de series de tiempo es la mejor técnica.
Bolsa de Valores
Los mercados de valores son los lugares donde los inversores individuales e institucionales se reúnen para comprar y vender acciones en un lugar público. Hoy en día, estos intercambios existen como mercados electrónicos.
Esa oferta y demanda ayudan a determinar el precio de cada valor o los niveles a los que los participantes del mercado de valores (inversores y comerciantes) están dispuestos a comprar o vender.
El concepto detrás de cómo funciona el mercado de valores es bastante simple. Operando de manera muy similar a una casa de subastas, el mercado de valores permite a compradores y vendedores negociar precios y realizar transacciones.
Definición de ‘stock’
Una acción o acción (también conocida como «capital» de una empresa) es un instrumento financiero que representa la propiedad de una empresa
Aprendizaje automático en el mercado de valores
El mercado de valores es muy impredecible, cualquier cambio geopolítico puede afectar la tendencia de las acciones en el mercado de acciones, recientemente hemos visto cómo covid-19 ha impactado los precios de las acciones, por lo que en los datos financieros es muy difícil hacer un análisis de tendencias confiable. . La forma más eficiente de resolver este tipo de problemas es con la ayuda del aprendizaje automático y el aprendizaje profundoEl aprendizaje profundo, una subdisciplina de la inteligencia artificial, se basa en redes neuronales artificiales para analizar y procesar grandes volúmenes de datos. Esta técnica permite a las máquinas aprender patrones y realizar tareas complejas, como el reconocimiento de voz y la visión por computadora. Su capacidad para mejorar continuamente a medida que se le proporcionan más datos la convierte en una herramienta clave en diversas industrias, desde la salud....
En este tutorial, resolveremos este problema con el modelo ARIMA.
Para conocer la estacionalidad, consulte mi blog anterior. Y para obtener una comprensión básica de ARIMA, le recomendaría que lea este blog, esto lo ayudará a comprender mejor cómo funciona el análisis de series temporales.
Implementar la previsión del precio de las acciones
Yo usaré nsepy biblioteca para extraer los datos históricos de SBIN.
Importaciones
import os
import warnings
warnings.filterwarnings('ignore')
from pylab import rcParams
rcParams['figure.figsize'] = 10, 6
from statsmodels.tsa.stattools import adfuller
from statsmodels.tsa.seasonal import seasonal_decompose
from statsmodels.tsa.arima_model import ARIMA
from pmdarima.arima import auto_arima
from sklearn.metrics import mean_squared_error, mean_absolute_error
import math
import numpy as np
from nsepy import get_history
from datetime import date
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
Run the below code to extract the historical data:
sbin = get_history(symbol="SBIN",
start=date(2000,1,1),
end=date(2020,11,1))
sbin.head()
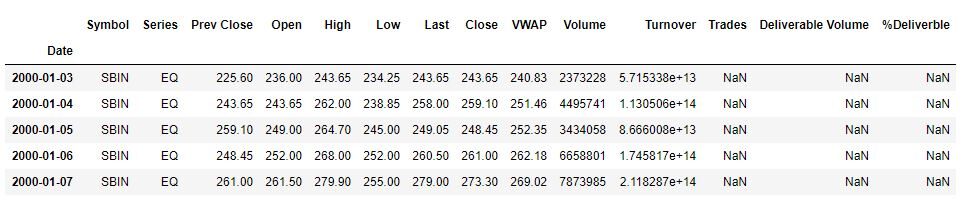
The data shows the stock price of SBIN from 2020-1-1 to 2020-11-1. The goal is to create a model that will forecast
the closing price of the stock.
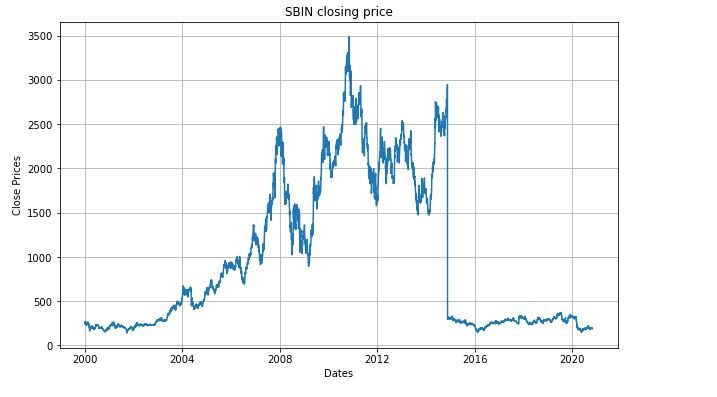
Creemos una visualización que mostrará el precio de cierre diario de la acción.
plt.figure(figsize=(10,6))
plt.grid(True)
plt.xlabel('Dates')
plt.ylabel('Close Prices')
plt.plot(sbin['Close'])
plt.title('SBIN closing price')
plt.show()
plt.figure(figsize=(10,6))
df_close = sbin['Close']
df_close.plot(style="k.")
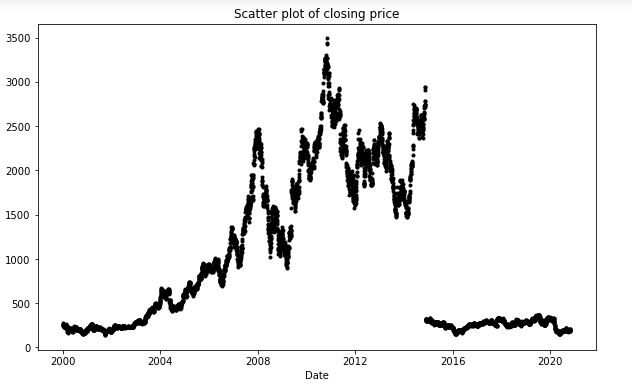
plt.title('Scatter plotUn diagrama de dispersión es una representación gráfica que muestra la relación entre dos variables. Cada punto en el gráfico corresponde a un par de valores, lo que permite identificar patrones, tendencias o correlaciones. Esta herramienta es útil en diversas disciplinas, como la estadística y la investigación científica, ya que facilita el análisis visual de datos y la comprensión de la relación entre los elementos estudiados.... of closing price')
plt.show()
plt.figure(figsize=(10,6))
df_close = sbin['Close']
df_close.plot(style="k.",kind='hist')
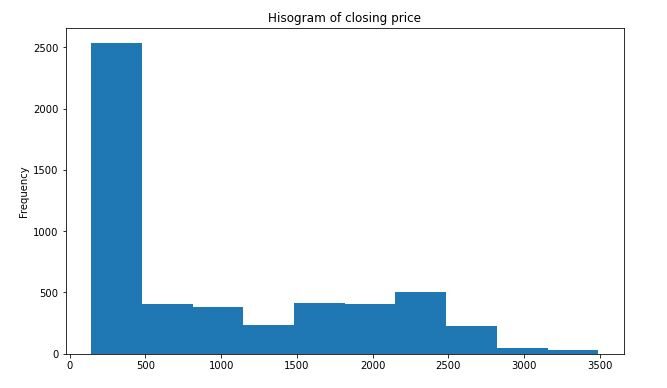
plt.title('Hisogram of closing price')
plt.show()
Primero, debemos verificar si una serie es estacionaria o no porque el análisis de series de tiempo solo funciona con datos estacionarios.
Prueba de estacionariedad:
Para identificar la naturaleza de los datos, usaremos la hipótesis nulaLa hipótesis nula es un concepto fundamental en la estadística que establece una afirmación inicial sobre un parámetro poblacional. Su propósito es ser probada y, en caso de ser refutada, permite aceptar la hipótesis alternativa. Este enfoque es esencial en la investigación científica, ya que proporciona un marco para evaluar la evidencia empírica y tomar decisiones basadas en datos. Su formulación y análisis son cruciales en estudios estadísticos.....
H0: La hipótesis nula: Es una declaración sobre la población que se cree que es cierta o se utiliza para presentar un argumento a menos que se pueda demostrar que es incorrecta más allá de una duda razonable.
H1: La hipótesis alternativa: Es una afirmación sobre la población que contradice H0 y lo que concluimos cuando rechazamos H0.
#Ho: no es estacionario
# H1: está parado
Si no rechazamos la hipótesis nula, podemos decir que la serie es no estacionaria. Esto significa que la serie puede ser lineal.
Si tanto la desviación estándar como la media son líneas planas (media constante y varianza constante), la serie se vuelve estacionaria.
from statsmodels.tsa.stattools import adfuller
def test_stationarity(timeseries):
#Determing rolling statistics
rolmean = timeseries.rolling(12).mean()
rolstd = timeseries.rolling(12).std()
#Plot rolling statistics:
plt.plot(timeseries, color="yellow",label="Original")
plt.plot(rolmean, color="red", label="Rolling Mean")
plt.plot(rolstd, color="black", label="Rolling Std")
plt.legend(loc="best")
plt.title('Rolling Mean and Standard Deviation')
plt.show(block=False)
print("Results of dickey fuller test")
adft = adfuller(timeseries,autolag='AIC')
# output for dft will give us without defining what the values are.
#hence we manually write what values does it explains using a for loop
output = pd.Series(adft[0:4],index=['Test Statistics','p-value','No. of lags used','Number of observations used'])
for key,values in adft[4].items():
output['critical value (%s)'%key] = values
print(output)
test_stationarity(sbin['Close'])
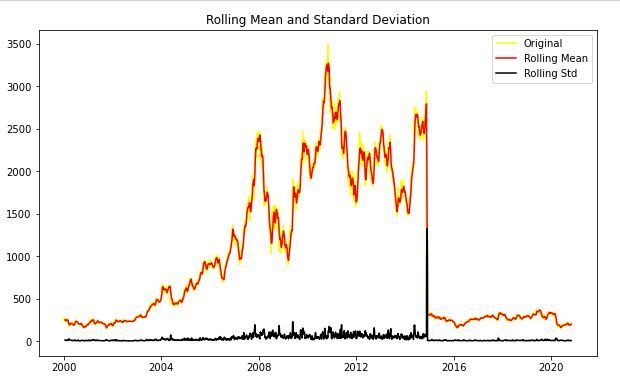
After analysing the above graph, we can see the increasing mean and standard deviation and hence our series is not stationary.
Results of dickey fuller test Test Statistics -1.914523 p-value 0.325260 No. of lags used 3.000000 Number of observations used 5183.000000 critical value (1%) -3.431612 critical value (5%) -2.862098 critical value (10%) -2.567067 dtype: float64
Vemos que el valor p es mayor que 0.05 por lo que no podemos rechazar el Hipótesis nula. Además, las estadísticas de la prueba son mayores que los valores críticos. por lo que los datos no son estacionarios.
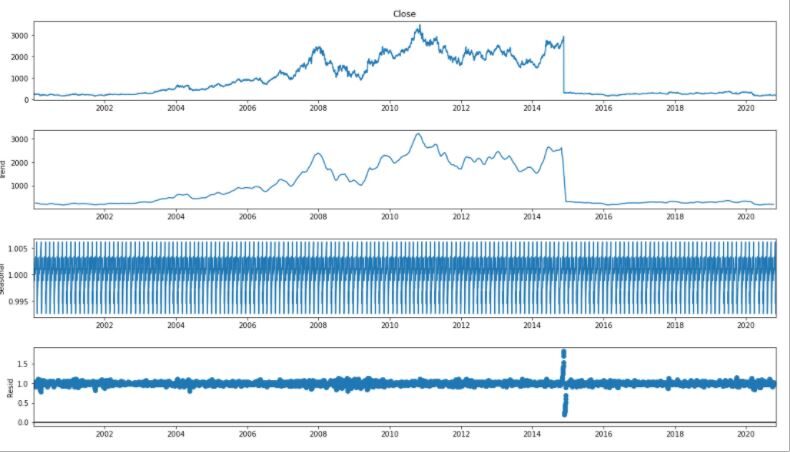
Para el análisis de series de tiempo, separamos Tendencia y Estacionalidad de las series de tiempo.
result = seasonal_decompose(df_close, model="multiplicative", freq = 30) fig = plt.figure() fig = result.plot() fig.set_size_inches(16, 9)
from pylab import rcParams
rcParams['figure.figsize'] = 10, 6
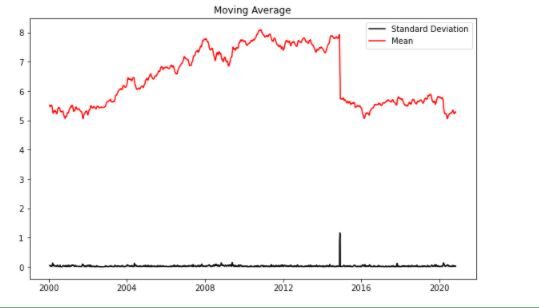
df_log = np.log(sbin['Close'])
moving_avg = df_log.rolling(12).mean()
std_dev = df_log.rolling(12).std()
plt.legend(loc="best")
plt.title('Moving Average')
plt.plot(std_dev, color ="black", label = "Standard Deviation")
plt.plot(moving_avg, color="red", label = "Mean")
plt.legend()
plt.show()
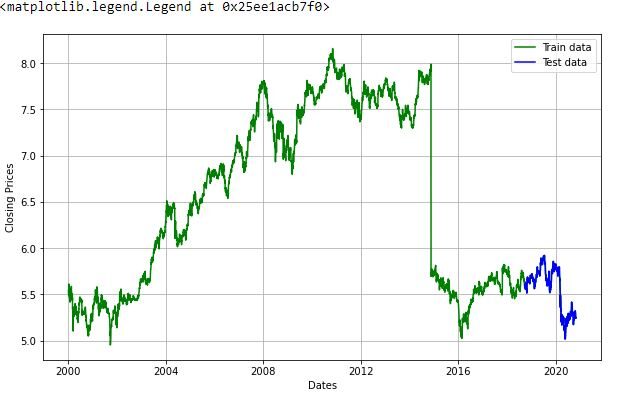
Ahora vamos a crear un modelo ARIMA y lo entrenaremos con el precio de cierre de la acción en los datos del tren. Así que dividamos los datos en entrenamientoEl entrenamiento es un proceso sistemático diseñado para mejorar habilidades, conocimientos o capacidades físicas. Se aplica en diversas áreas, como el deporte, la educación y el desarrollo profesional. Un programa de entrenamiento efectivo incluye la planificación de objetivos, la práctica regular y la evaluación del progreso. La adaptación a las necesidades individuales y la motivación son factores clave para lograr resultados exitosos y sostenibles en cualquier disciplina.... y conjunto de prueba y visualícelos.
train_data, test_data = df_log[3:int(len(df_log)*0.9)], df_log[int(len(df_log)*0.9):]
plt.figure(figsize=(10,6))
plt.grid(True)
plt.xlabel('Dates')
plt.ylabel('Closing Prices')
plt.plot(df_log, 'green', label="Train data")
plt.plot(test_data, 'blue', label="Test data")
plt.legend()
model_autoARIMA = auto_arima(train_data, start_p=0, start_q=0, test="adf", # use adftest to find optimal 'd' max_p=3, max_q=3, # maximum p and q m=1, # frequency of series d=None, # let model determine 'd' seasonal=False, # No Seasonality start_P=0, D=0, trace=True, error_action='ignore', suppress_warnings=True, stepwise=True) print(model_autoARIMA.summary())
Performing stepwise search to minimize aic
ARIMA(0,1,0)(0,0,0)[0] intercept : AIC=-16607.561, Time=2.19 sec
ARIMA(1,1,0)(0,0,0)[0] intercept : AIC=-16607.961, Time=0.95 sec
ARIMA(0,1,1)(0,0,0)[0] intercept : AIC=-16608.035, Time=2.27 sec
ARIMA(0,1,0)(0,0,0)[0] : AIC=-16609.560, Time=0.39 sec
ARIMA(1,1,1)(0,0,0)[0] intercept : AIC=-16606.477, Time=2.77 sec
Best model: ARIMA(0,1,0)(0,0,0)[0]
Total fit time: 9.079 seconds
SARIMAX Results
==============================================================================
Dep. Variable: y No. Observations: 4665
Model: SARIMAX(0, 1, 0) Log Likelihood 8305.780
Date: Tue, 24 Nov 2020 AIC -16609.560
Time: 20:08:50 BIC -16603.113
Sample: 0 HQIC -16607.293
- 4665
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
sigma2 0.0017 1.06e-06 1566.660 0.000 0.002 0.002
===================================================================================
Ljung-Box (Q): 24.41 Jarque-Bera (JB): 859838819.58
Prob(Q): 0.98 Prob(JB): 0.00
Heteroskedasticity (H): 7.16 Skew: -37.54
Prob(H) (two-sided): 0.00 Kurtosis: 2105.12
===================================================================================
model_autoARIMA.plot_diagnostics(figsize=(15,8)) plt.show()
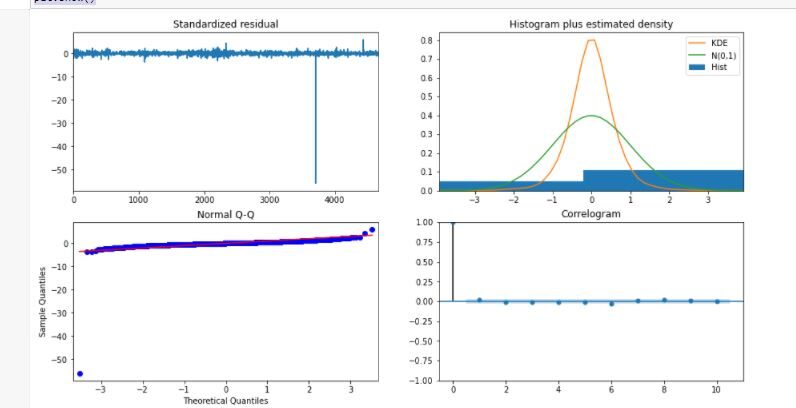
model = ARIMA(train_data, order=(3, 1, 2)) fitted = model.fit(disp=-1) print(fitted.summary())
ARIMA Model Results
==============================================================================
Dep. Variable: D.Close No. Observations: 4664
Model: ARIMA(3, 1, 2) Log Likelihood 8309.178
Method: css-mle S.D. of innovations 0.041
Date: Tue, 24 Nov 2020 AIC -16604.355
Time: 20:09:37 BIC -16559.222
Sample: 1 HQIC -16588.481
=================================================================================
coef std err z P>|z| [0.025 0.975]
---------------------------------------------------------------------------------
const 8.761e-06 0.001 0.015 0.988 -0.001 0.001
ar.L1.D.Close 1.3689 0.251 5.460 0.000 0.877 1.860
ar.L2.D.Close -0.7118 0.277 -2.567 0.010 -1.255 -0.168
ar.L3.D.Close 0.0094 0.021 0.445 0.657 -0.032 0.051
ma.L1.D.Close -1.3468 0.250 -5.382 0.000 -1.837 -0.856
ma.L2.D.Close 0.6738 0.282 2.391 0.017 0.122 1.226
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
AR.1 0.9772 -0.6979j 1.2008 -0.0987
AR.2 0.9772 +0.6979j 1.2008 0.0987
AR.3 74.0622 -0.0000j 74.0622 -0.0000
MA.1 0.9994 -0.6966j 1.2183 -0.0969
MA.2 0.9994 +0.6966j 1.2183 0.0969
-----------------------------------------------------------------------------
# Forecast fc, se, conf = fitted.forecast(519, alpha=0.05) # 95% confidence
fc_series = pd.Series(fc, index=test_data.index)
lower_series = pd.Series(conf[:, 0], index=test_data.index)
upper_series = pd.Series(conf[:, 1], index=test_data.index)
plt.figure(figsize=(12,5), dpi=100)
plt.plot(train_data, label="training")
plt.plot(test_data, color="blue", label="Actual Stock Price")
plt.plot(fc_series, color="orange",label="Predicted Stock Price")
plt.fill_between(lower_series.index, lower_series, upper_series,
color="k", alpha=.10)
plt.title('SBIN Stock Price Prediction')
plt.xlabel('Time')
plt.ylabel('Actual Stock Price')
plt.legend(loc="upper left", fontsize=8)
plt.show()
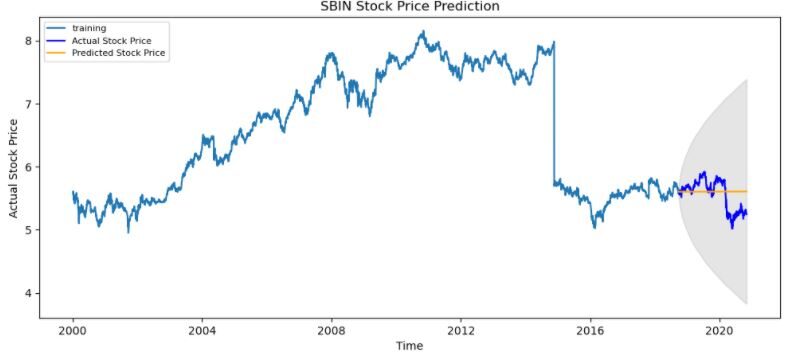
Conclusión
El pronóstico de series de tiempo es realmente útil cuando tenemos que tomar decisiones futuras o tenemos que hacer análisis, podemos hacerlo rápidamente usando ARIMA, hay muchos otros modelos de los que podemos hacer el pronóstico de series de tiempo, pero ARIMA es realmente fácil de entender.
Espero que este artículo te ayude y te ahorre una buena cantidad de tiempo. Déjame saber si tienes alguna sugerencia.
FELIZ CODIFICACIÓN.
Prabhat Pathak (Perfil de Linkedin) es analista senior y entusiasta de la innovación.






