Predicción de supervivencia del Titanic | Tu primer proyecto de ciencia de datos

Introducción

En este artículo, revisaremos el popular conjunto de datos del Titanic y trataremos de predecir si una persona sobrevivió al naufragio. Puede obtener este conjunto de datos de Kaggle, vinculado aquí. Este artículo se centrará en cómo pensar sobre estos proyectos, más que en la implementación. Muchos de los principiantes están confundidos sobre cómo comenzar, cuándo terminar y todo lo demás, espero que este artículo sirva como un manual para principiantes para ti. Te sugiero que practiques el proyecto en Kaggle.

El objetivo: predecir si un pasajero sobrevivió o no. 0 por no sobrevivir, 1 por sobrevivir.

Describiendo los datos

En este artículo, haremos un análisis de datos básico, luego un poco de ingeniería de características y, al final, utilizaremos algunos de los modelos populares para la predicción. Empecemos.

Análisis de los datos

Paso 1: Importación de bibliotecas básicas

import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline

Paso 2: leer los datos

training = pd.read_csv('/kaggle/input/titanic/train.csv')
test = pd.read_csv('/kaggle/input/titanic/test.csv')

training['train_test'] = 1
test['train_test'] = 0
test['Survived'] = np.NaN
all_data = pd.concat([training,test])

all_data.columns

Paso 3: exploración de datos

En esta sección, intentaremos extraer conocimientos de los datos y familiarizarnos con ellos para poder crear modelos más eficientes.

training.info()

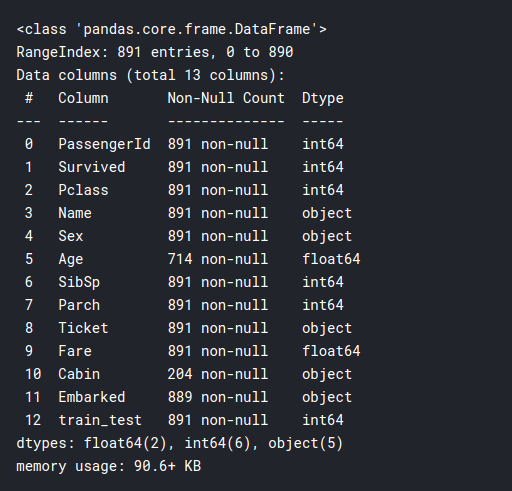
training.describe()

# seperate the data into numeric and categorical
df_num = training[['Age','SibSp','Parch','Fare']]
df_cat = training[['Survived','Pclass','Sex','Ticket','Cabin','Embarked']]

Ahora hagamos gráficos de los datos numéricos:

for i in df_num.columns:
    plt.hist(df_num[i])
    plt.title(i)
    plt.show()

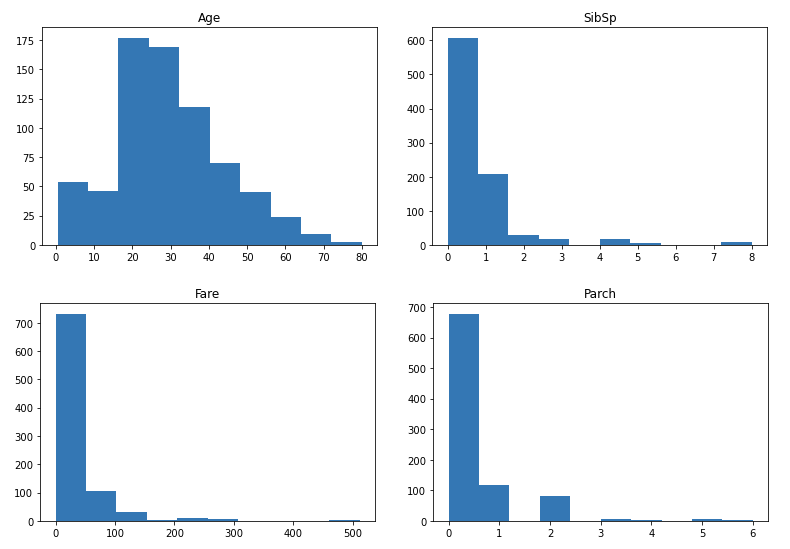
Entonces, como puede ver, la mayoría de las distribuciones están dispersas, excepto Age, está bastante normalizado. Podríamos considerar normalizarlos más adelante. A continuación, trazamos un mapa de calorUn "mapa de calor" es una representación gráfica que utiliza colores para mostrar la densidad de datos en un área específica. Comúnmente utilizado en análisis de datos, marketing y estudios de comportamiento, este tipo de visualización permite identificar patrones y tendencias rápidamente. A través de variaciones cromáticas, los mapas de calor facilitan la interpretación de grandes volúmenes de información, ayudando a la toma de decisiones informadas.... de correlación entre las columnas numéricas:

sns.heatmap(df_num.corr())

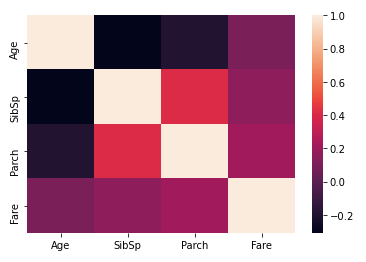
Aquí podemos ver que Parch y SibSp tienen una correlación más alta, lo que generalmente tiene sentido ya que es más probable que los padres viajen con sus múltiples hijos y los cónyuges tienden a viajar juntos. A continuación, comparemos las tasas de supervivencia entre las variables numéricas. Esto podría revelar algunas ideas interesantes:

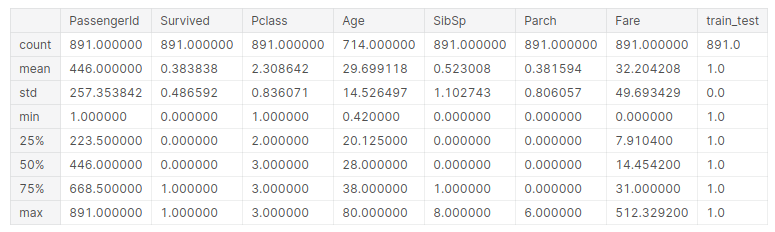
pd.pivot_table(training, index = 'Survived', values = ['Age','SibSp','Parch','Fare'])

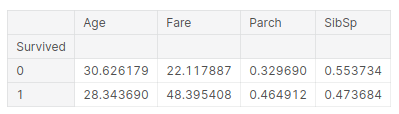
La inferencia que podemos sacar de esta tabla es:

1. La edad promedio de los sobrevivientes es de 28 años, por lo que los jóvenes tienden a sobrevivir más.
2. Las personas que pagaban tarifas más altas tenían más probabilidades de sobrevivir, más del doble. Esta podría ser la gente que viaja en primera clase. Así sobrevivieron los ricos, lo cual es una historia triste en este escenario.
3. En la tercera columna, si tiene padres, tiene una mayor probabilidad de sobrevivir. Entonces, los padres podrían haber salvado a los niños antes que ellos mismos, explicando así las tarifas
4. Y si eres un niño y tienes hermanos, tienes menos posibilidades de sobrevivir.

Ahora hacemos algo similar con nuestras variables categóricas:

for i in df_cat.columns:
    sns.barplot(df_cat[i].value_counts().index,df_cat[i].value_counts()).set_title(i)
    plt.show()

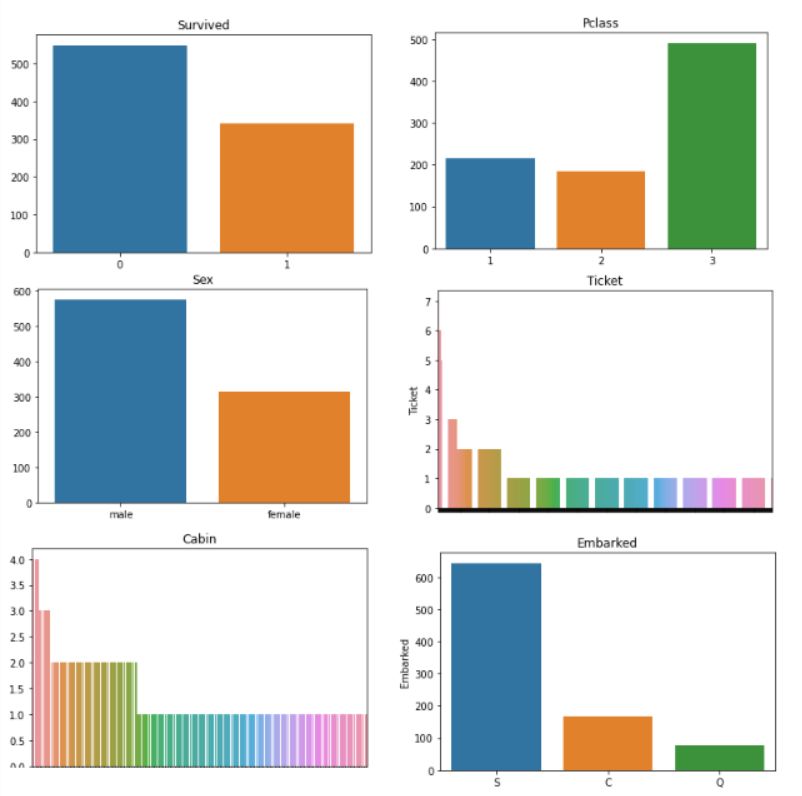
Los gráficos de Ticket y Cabin se ven muy desordenados, ¡es posible que tengamos que diseñarlos! Aparte de eso, el resto de los gráficos nos dice:

1. Sobrevivido: la mayoría de las personas murieron en el naufragio, solo unas 300 personas sobrevivieron.
2. Pclass: La mayoría de las personas que viajaban tenían boletos para la 3ra clase.
3. Sexo: había más hombres que mujeres a bordo del barco, aproximadamente el doble de la cantidad.
4. Embarcado: La mayoría de los pasajeros abordaron el barco desde Southampton.

Ahora haremos algo similar a la tabla dinámicaLa tabla dinámica es una herramienta poderosa en programas de hoja de cálculo, como Microsoft Excel y Google Sheets. Permite resumir, analizar y visualizar grandes volúmenes de datos de manera eficiente. A través de su interfaz intuitiva, los usuarios pueden reorganizar la información, aplicar filtros y crear informes personalizados, facilitando la toma de decisiones informadas en diversos contextos, desde el ámbito empresarial hasta la investigación académica.... anterior, pero con nuestras variables categóricas, y las compararemos con nuestra variableEn estadística y matemáticas, una "variable" es un símbolo que representa un valor que puede cambiar o variar. Existen diferentes tipos de variables, como las cualitativas, que describen características no numéricas, y las cuantitativas, que representan cantidades numéricas. Las variables son fundamentales en experimentos y estudios, ya que permiten analizar relaciones y patrones entre diferentes elementos, facilitando la comprensión de fenómenos complejos.... dependiente, que es si la gente sobrevivió:

print(pd.pivot_table(training, index = 'Survived', columns="Pclass",
                     values="Ticket" ,aggfunc="count"))
print()
print(pd.pivot_table(training, index = 'Survived', columns="Sex", 
                     values="Ticket" ,aggfunc="count"))
print()
print(pd.pivot_table(training, index = 'Survived', columns="Embarked", 
                     values="Ticket" ,aggfunc="count"))

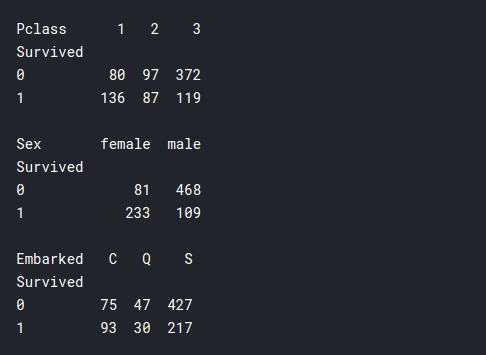
1. Pclass: Aquí podemos ver que sobrevivieron muchas más personas de la Primera clase que de la Segunda o la Tercera clase, a pesar de que el número total de pasajeros en la Primera clase fue mucho menor que en la Tercera clase. Por lo tanto, aquí se confirma nuestra suposición anterior de que los ricos sobrevivieron, lo que podría ser relevante para la construcción de modelos.
2. Sexo: la mayoría de las mujeres sobrevivieron y la mayoría de los hombres murieron en el naufragio. Por lo tanto, parece que el dicho «La mujer y los niños primero» se aplica realmente en este escenario.
3. Embarcado: Esto no parece muy relevante, tal vez si alguien fuera de «Cherburgo”Tenía una mayor probabilidad de sobrevivir.

Paso 4: Ingeniería de funciones

Vimos que nuestro billete y cabina los datos realmente no tienen sentido para nosotros, y esto podría obstaculizar el rendimiento de nuestro modelo, por lo que tenemos que simplificar algunos de estos datos con la ingeniería de funciones.

Si miramos los datos reales de la cabina, vemos que básicamente hay una letra y luego un número. Las letras pueden significar qué tipo de camarote es, en qué parte del barco se encuentra, en qué piso, para qué clase es, etc. Y los números pueden significar el número de camarote. Primero dividámoslos en cabinas individuales y veamos si alguien tenía más de una cabina.

df_cat.Cabin
training['cabin_multiple'] = training.Cabin.apply(lambda x: 0 if pd.isna(x) 
                                                    else len(x.split(' ')))
training['cabin_multiple'].value_counts()

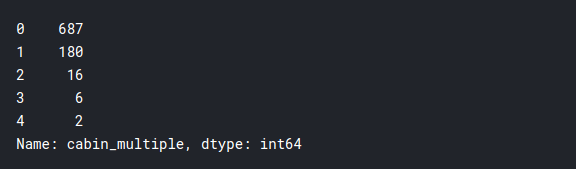
Parece que la gran mayoría no tenía cabañas individuales, y solo unas pocas personas tenían más de una cabaña. Ahora veamos si las tasas de supervivencia dependen de esto:

pd.pivot_table(training, index = 'Survived', columns="cabin_multiple",
               values="Ticket" ,aggfunc="count")

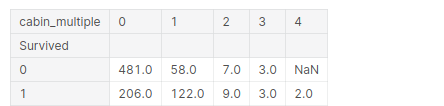
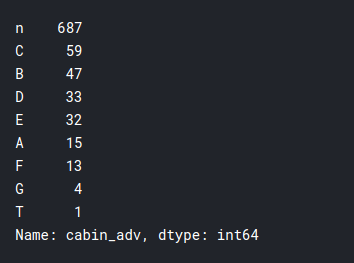
A continuación, veamos la letra real de la cabaña en la que se encontraban. Por lo tanto, podría esperar que las cabañas con la misma letra estén aproximadamente en las mismas ubicaciones o en los mismos pisos y, lógicamente, si una cabaña estuviera cerca de los botes salvavidas, tenían más posibilidades de sobrevivir. Echemos un vistazo a eso:

# n stands for null
# in this case we will treat null values like it's own category
training['cabin_adv'] = training.Cabin.apply(lambda x: str(x)[0])
#comparing survival rates by cabin
print(training.cabin_adv.value_counts())
pd.pivot_table(training,index='Survived',columns="cabin_adv", 
                        values="Name", aggfunc="count")

Hice algo de ingeniería futura en el billete columna y no arrojó muchos conocimientos importantes, que aún no conocemos, por lo que omitiré esa parte para mantener el artículo conciso. Simplemente dividiremos los tickets en numéricos y no numéricos para un uso eficiente:

training['numeric_ticket'] = training.Ticket.apply(lambda x: 1 if x.isnumeric() else 0)
training['ticket_letters'] = training.Ticket.apply(lambda x: ''.join(x.split(' ')[:-1])
                                            .replace('.','').replace('/','')
                                            .lower() if len(x.split(' ')[:-1]) >0 else 0)

Otra cosa interesante que podemos observar es el título de pasajeros individuales. Y si jugó algún papel en que consiguieran un asiento en los botes salvavidas.

training.Name.head(50)
training['name_title'] = training.Name.apply(lambda x: x.split(',')[1]
                                                        .split('.')[0].strip())
training['name_title'].value_counts()

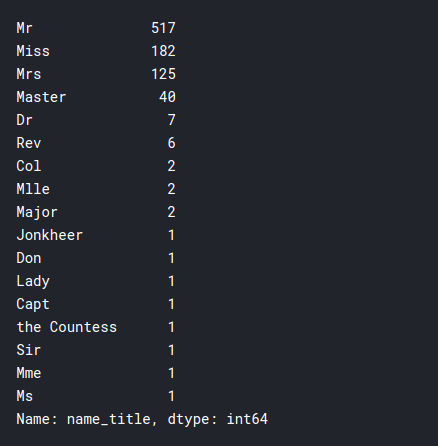
Como puede ver, el barco fue abordado por personas de muchas clases diferentes, esto podría sernos útil en nuestro modelo.

Paso 5: preprocesamiento de datos para el modelo

En este segmento, preparamos nuestros datos para modelos. Los objetivos que tenemos que cumplir se enumeran a continuación:

1. Elimine los valores nulos de la columna Embarcado
2. Incluya solo datos relevantes
3. Transforme categóricamente todos los datos, usando algo llamado transformador.
4. Imputar datos con las tendencias centrales por edad y tarifa.
5. Normalizar el tarifa columna para tener una distribución más normal.
6. utilizando datos de escala de escala estándar 0-1

Paso 6: Implementación del modelo

Aquí simplemente implementaremos los diversos modelos con parámetrosLos "parámetros" son variables o criterios que se utilizan para definir, medir o evaluar un fenómeno o sistema. En diversos campos como la estadística, la informática y la investigación científica, los parámetros son fundamentales para establecer normas y estándares que guían el análisis y la interpretación de datos. Su adecuada selección y manejo son cruciales para obtener resultados precisos y relevantes en cualquier estudio o proyecto.... predeterminados y veremos cuál produce el mejor resultado. Los modelos se pueden ajustar aún más para un mejor rendimiento, pero no están en el alcance de este artículo. Los modelos que ejecutaremos son:

• Regresión logística
• K Vecino más cercano
• Clasificador de vectores de soporte

Primero, importamos los modelos necesarios

from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC

1) Regresión logística

lr = LogisticRegression(max_iter = 2000)
cv = cross_val_score(lr,X_train_scaled,y_train,cv=5)
print(cv)
print(cv.mean())

2) K Vecino más cercano

knn = KNeighborsClassifier()
cv = cross_val_score(knn,X_train_scaled,y_train,cv=5)
print(cv)
print(cv.mean())

3) Clasificador de vectores de soporte

svc = SVC(probability = True)
cv = cross_val_score(svc,X_train_scaled,y_train,cv=5)
print(cv)
print(cv.mean())

Por tanto, la precisión de los modelos es:

• Regresión logística: 82,2%
• K Vecino más cercano: 81,4%
• SVC: 83,3%

Como puede ver, obtenemos una precisión decente con todos nuestros modelos, pero el mejor es SVC. ¡Y listo, así ha completado su primer proyecto de ciencia de datos! Aunque se puede hacer mucho más para obtener mejores resultados, esto es más que suficiente para ayudarlo a comenzar y ver cómo piensa como un científico de datos. Espero que este tutorial te haya ayudado, me lo pasé muy bien haciendo el proyecto yo mismo y espero que tú también lo disfrutes. ¡¡Salud!!

Relacionado