Estadísticas de pedidos | ¿Qué son las estadísticas de pedidos?

Introducción

La estadística de pedidos es un concepto muy útil en las ciencias estadísticas. Tienen una amplia gama de aplicaciones que incluyen modelado de subastas, carreras de autos y pólizas de seguros, optimización de procesos de producción, estimación de parámetrosLos "parámetros" son variables o criterios que se utilizan para definir, medir o evaluar un fenómeno o sistema. En diversos campos como la estadística, la informática y la investigación científica, los parámetros son fundamentales para establecer normas y estándares que guían el análisis y la interpretación de datos. Su adecuada selección y manejo son cruciales para obtener resultados precisos y relevantes en cualquier estudio o proyecto.... de distribuciones, et al. A través de este artículo, entenderemos la idea de las estadísticas de pedidos. Primero entenderemos su significado y gradualmente procederemos a su distribución, cubriendo eventualmente conceptos más avanzados.

Supongamos que tenemos un conjunto de variables aleatorias X₁, X₂, …, X_norte, que son independientes e idénticamente distribuidos (iid). Por independencia, queremos decir que el valor tomado por una variableEn estadística y matemáticas, una "variable" es un símbolo que representa un valor que puede cambiar o variar. Existen diferentes tipos de variables, como las cualitativas, que describen características no numéricas, y las cuantitativas, que representan cantidades numéricas. Las variables son fundamentales en experimentos y estudios, ya que permiten analizar relaciones y patrones entre diferentes elementos, facilitando la comprensión de fenómenos complejos.... aleatoria no está influenciado por los valores tomados por otras variables aleatorias. Por distribución idéntica, queremos decir que la función de densidad de probabilidad (PDF) (o de manera equivalente, la función de distribución acumulativa, CDF) para las variables aleatorias es la misma. La K^th La estadística de orden para este conjunto de variables aleatorias se define como k^th valor más pequeño de la muestra.

Para comprender mejor este concepto, tomaremos 5 variables aleatorias X₁, X₂, X₃, X₄, X₅. Observaremos una realización / resultado aleatorio de la distribución de cada una de estas variables aleatorias. Supongamos que obtenemos los siguientes valores:

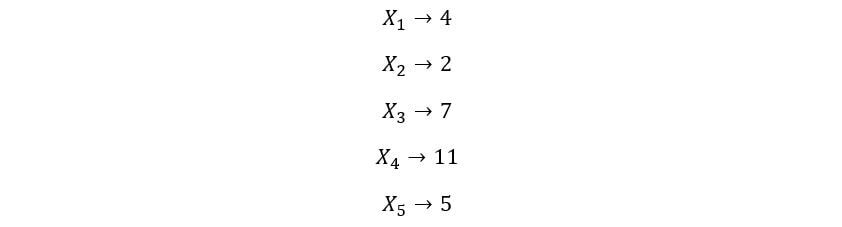
La K^th la estadística de orden para este experimento es la k^th valor más pequeño del conjunto {4, 2, 7, 11, 5}. Entonces, el 1^{S t} la estadística de orden es 2 (valor más pequeño), la 2^{Dakota del Norte} la estadística de orden es 4 (la siguiente más pequeña), y así sucesivamente. El 5^th el estadístico de orden es el quinto valor más pequeño (el valor más grande), que es 11. Repetimos este proceso muchas veces, es decir, extraemos muestras de la distribución de cada una de estas iid variables aleatorias y encontramos la k^th valor más pequeño para cada conjunto de observaciones. La distribución de probabilidad de estos valores da la distribución de k^th estadísticas de pedidos.

En general, si ordenamos variables aleatorias X₁, X₂, …, X_norte en orden ascendente, entonces la k^th la estadística de orden se muestra como:

La notación general de la k^th la estadística de orden es X_(k). Nota X_(k) es diferente de X_k. X_k es la k^th variable aleatoria de nuestro conjunto, mientras que X_(k) es la k^th orden estadística de nuestro conjunto. X_(k) toma el valor de X_k si X_k es la k^th Variable aleatoria cuando las realizaciones se ordenan en orden ascendente.

El 1^{S t} estadística de orden X₍₁₎ es el conjunto de los valores mínimos de la realización del conjunto de ‘n’ variables aleatorias. Luego^th estadística de orden X_(norte) es el conjunto de los valores máximos (n-ésimo valores mínimos) de la realización del conjunto de ‘n’ variables aleatorias. Pueden expresarse como:

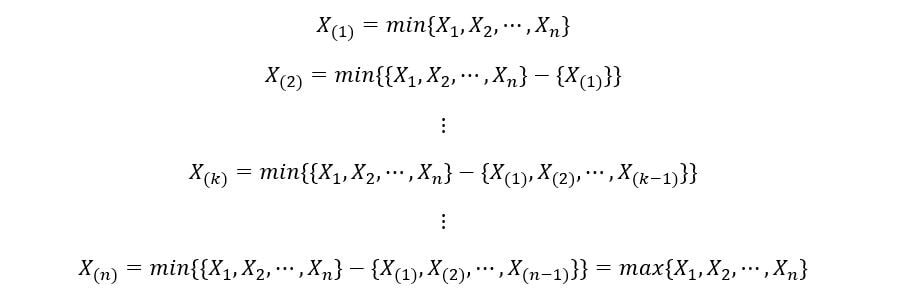
Distribución de estadísticas de pedidos

Ahora intentaremos averiguar la distribución de las estadísticas de pedidos. Primero describiremos la distribución de la n^th estadística de orden, luego el 1^{S t} orden estadística y finalmente la k^th estadística de orden en general.

A) Distribución de la n^th Estadística de pedidos:

Dejemos que la función de densidad de probabilidad (PDF) y la función de distribución acumulativa (CDF) nuestras variables aleatorias sean f_X(x) y F_X(x) respectivamente. Por definición de CDF,

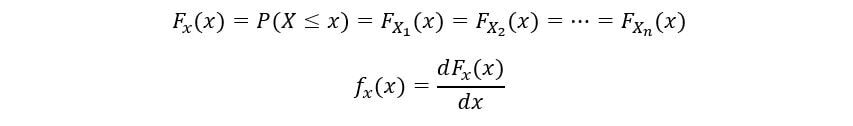
Dado que nuestras variables aleatorias se distribuyen de manera idéntica, tienen el mismo PDF f_X(x) y CDF F_X(X). Ahora calcularemos la CDF de n^th estadística de orden (F_norte(x)) como sigue:

Las variables aleatorias X₁, X₂, …, X_norte también son independientes. Por tanto, por propiedad de la independencia,

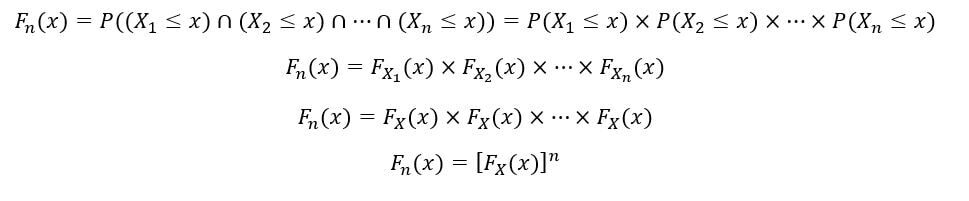
El PDF de la n^th orden estadístico (f_norte(x)) se calcula de la siguiente manera:

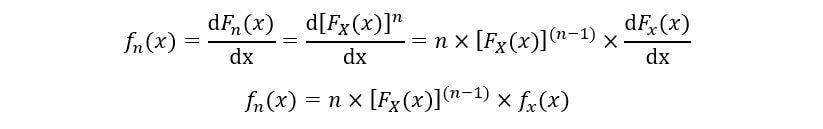
Por lo tanto, la expresión para PDF y CDF de n^th Se ha obtenido la estadística de orden.

B) Distribución del 1^{S t} Estadística de pedidos:

La CDF de una variable aleatoria también se puede calcular como el uno menos la probabilidad de que la variable aleatoria X tome un valor mayor o igual que x. Matemáticamente,

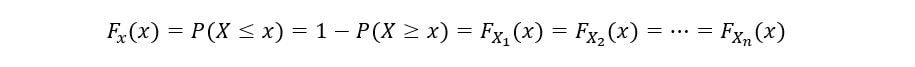
Determinaremos el CDF de 1^{S t} estadística de orden (F₁(x)) como sigue:

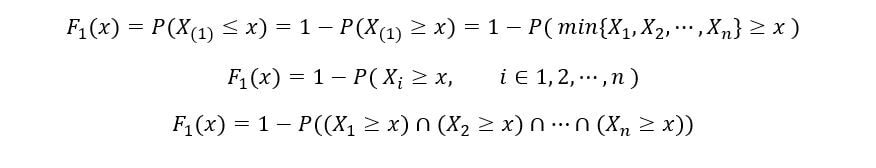
Una vez más, utilizando la propiedad de independencia de las variables aleatorias,

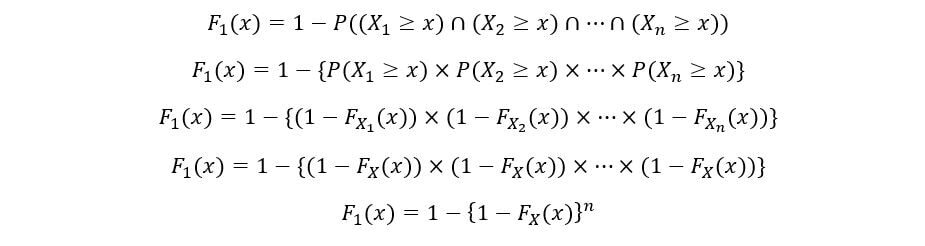
El PDF del 1^{S t} orden estadístico (f₁(x)) se calcula de la siguiente manera:

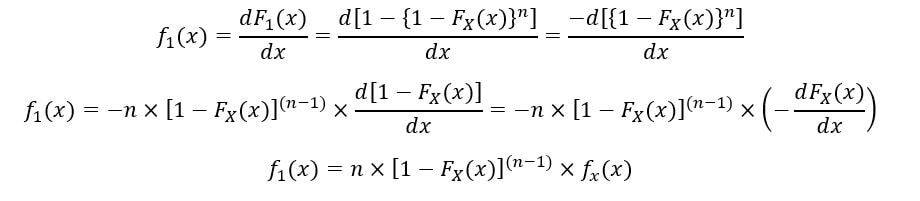
Por lo tanto, la expresión para PDF y CDF de 1^{S t} Se ha obtenido la estadística de orden.

C) Distribución de la k^th Estadística de pedidos:

Tenedor^th estadística de orden, en general, la siguiente ecuación describe su CDF (F_k(X)):

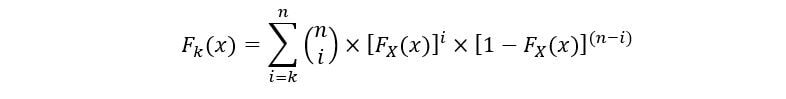
El PDF de k^th orden estadístico (f_k(x)) se expresa como:

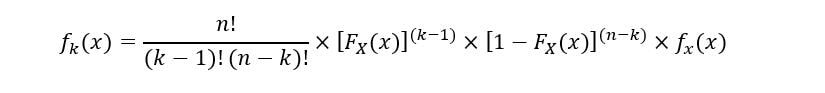
Para evitar confusiones, usaremos pruebas geométricas para entender la ecuación. Como se discutió anteriormente, el conjunto de variables aleatorias tiene el mismo PDF (f_X(X)). El siguiente gráfico muestra un PDF de muestra con la k^th Estadística de orden obtenida de un muestreo aleatorio:

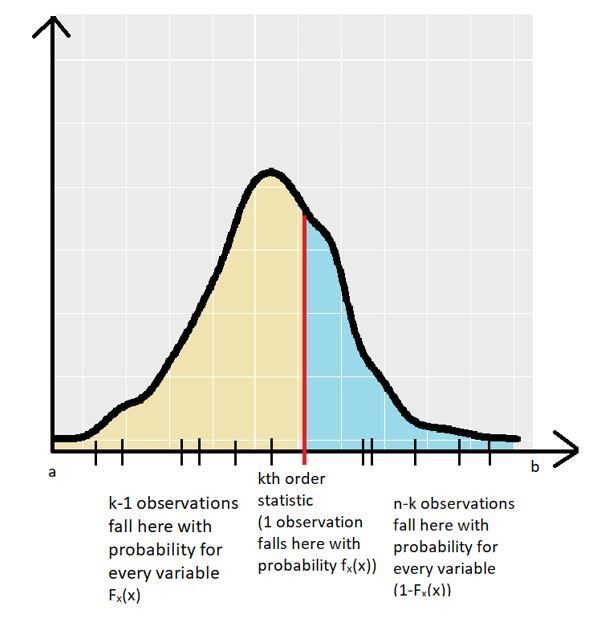
Entonces, la PDF de las variables aleatorias f_X(x) se define entre el intervalo [a,b]. El estadístico de k-ésimo orden para una muestra aleatoria se muestra con la línea roja. Las otras realizaciones variables (para la muestra aleatoria) se muestran mediante las pequeñas líneas negras en el eje x.

Hay exactamente (k – 1) observaciones de variables aleatorias que caen en la región amarilla del gráfico (la región entre a & k^th estadística de orden). La probabilidad de que una observación particular caiga en esta región está dada por la CDF de las variables aleatorias (F_X(X)). Pero somos conscientes de que (k – 1) observaciones cayeron en la región, lo que nos da el término (por independencia) (F_X(X))^{(k – 1)}.

Hay exactamente (n – k) observaciones de variables aleatorias que caen en la región azul del gráfico (la región entre k^th orden estadística & b). La probabilidad de que una observación particular caiga en esta región viene dada por el 1 – CDF de las variables aleatorias (1– F_X(X)). Pero somos conscientes de que (n – k) observaciones cayeron en la región, lo que nos da el término (por independencia) (1-F_X(X))^{(n – k)}.

Finalmente, exactamente 1 observación cae exactamente en el estadístico de k-ésimo orden con probabilidad f_X(X). Por lo tanto, el producto de los 3 términos nos da una idea del significado geométrico de la ecuación para PDF del estadístico de k-ésimo orden. Pero, ¿de dónde viene el término factorial? El escenario anterior solo mostró uno de los muchos ordenamientos. Puede haber muchas de estas combinaciones. El número total de tales combinaciones se muestra a continuación:

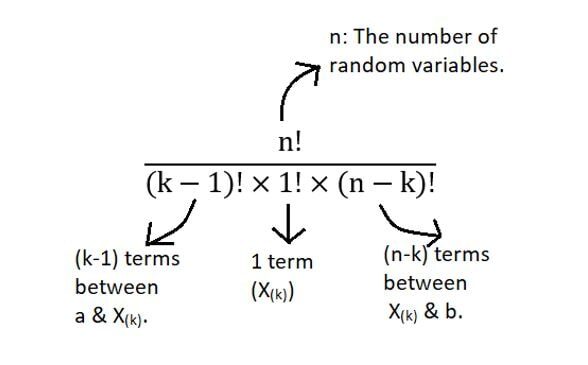
Por tanto, el producto de todos estos términos nos da la distribución general de k^th estadística de pedidos.

Funciones útiles de las estadísticas de pedidos

Las estadísticas de pedidos dan lugar a varias funciones útiles. Entre ellos, los notables incluyen el rango de la muestra y la medianaLa mediana es una medida estadística que representa el valor central de un conjunto de datos ordenados. Para calcularla, se organizan los datos de menor a mayor y se identifica el número que se encuentra en el medio. Si hay un número par de observaciones, se promedia los dos valores centrales. Este indicador es especialmente útil en distribuciones asimétricas, ya que no se ve afectado por valores extremos.... de la muestra.

1) Rango de muestra: Se define como la diferencia entre el valor más grande y el más pequeño. Se expresa de la siguiente manera:

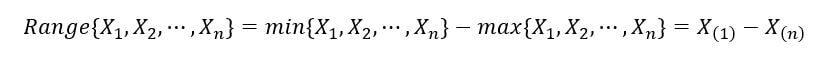
2) Mediana de la muestra: La mediana de la muestra divide la muestra aleatoria (realizaciones del conjunto de variables aleatorias) en dos mitades, una que contiene las muestras con valores más bajos y la otra que contiene las muestras con valores más altos. Es como la estadística de orden medio / central. Se define matemáticamente como:

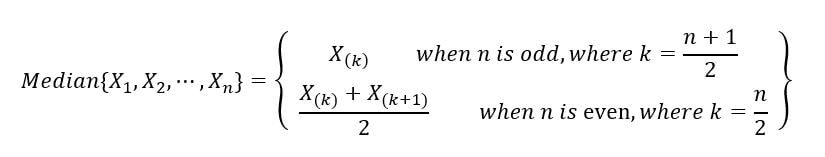
PDF conjunto de estadísticas de pedidos

Una función de densidad de probabilidad conjunta puede ayudarnos a comprender mejor la relación entre dos variables aleatorias (estadísticas de dos órdenes
en nuestro caso). El PDF conjunto para cualquier estadística de 2 órdenes X_(a) & X_(B), tal que 1 ≤ a ≤ b ≤ n viene dado por la siguiente ecuación:

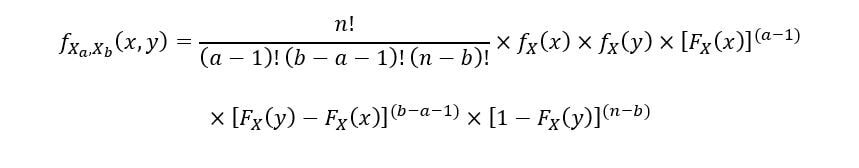
Ejemplo

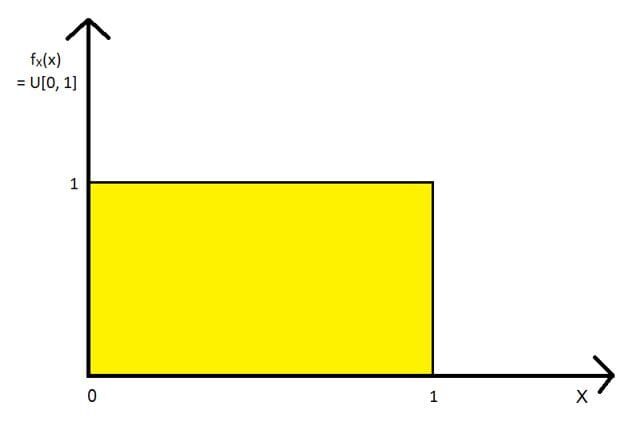
Usaremos un ejemplo muy simple para ilustrar la distribución de las estadísticas de orden: la distribución uniforme estándar (U[0, 1] distribución). Tomaremos 5 variables aleatorias X₁, X₂, X₃, X₄, X₅, todos tienen la U[0, 1] distribución. Para este conjunto de variables aleatorias, calcularemos y trazaremos el 1^{S t}, 3^rd (la mediana de la muestra) y 5^th (norte^th) estadísticas de pedidos. La siguiente figura"Figura" es un término que se utiliza en diversos contextos, desde el arte hasta la anatomía. En el ámbito artístico, se refiere a la representación de formas humanas o animales en esculturas y pinturas. En la anatomía, designa la forma y estructura del cuerpo. Además, en matemáticas, "figura" se relaciona con las formas geométricas. Su versatilidad hace que sea un concepto fundamental en múltiples disciplinas.... muestra la U[0, 1] distribución:

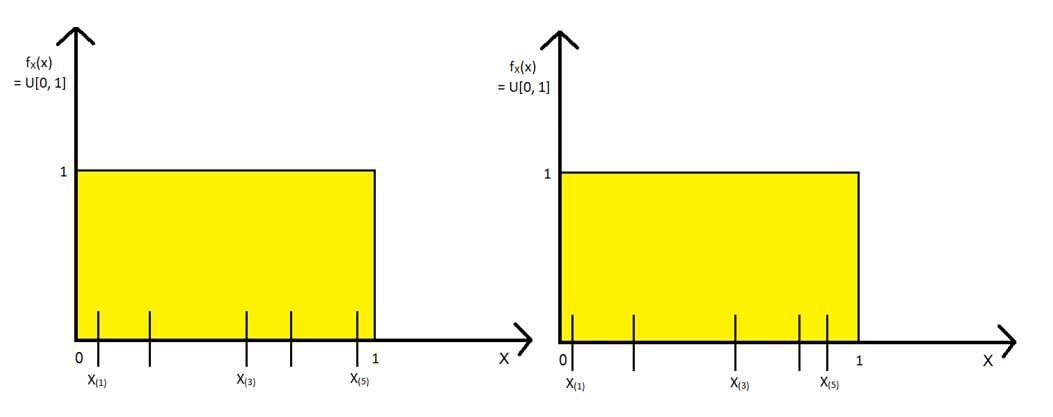
Dibujaremos muestras aleatorias de la siguiente manera y encontraremos el 1^{S t}, 3^rd & 5^th estadística de orden para cada muestra. A continuación se muestran dos de las muestras:

El PDF y CDF de distribución uniforme estándar se dan como:

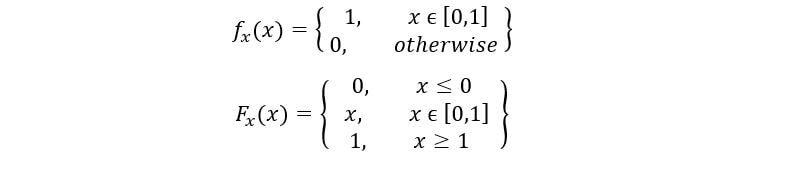
Usaremos esta información y calcularemos X₍₁₎, X₍₃₎ & X₍₅₎ usando las fórmulas que derivamos. Tomaremos el caso solo cuando x esté entre 0 y 1 (para otros casos, la estadística de orden es cero ya que PDF es cero).

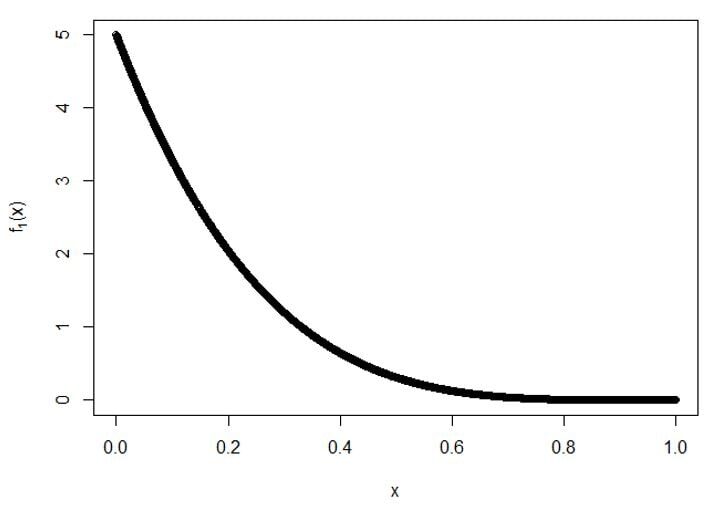
A) Para 1^{S t} estadística de orden:

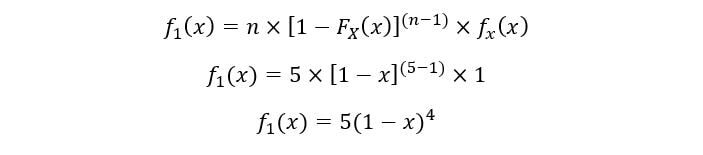
Trazar para f₁(X):

B) Para 3^rd estadística de orden:

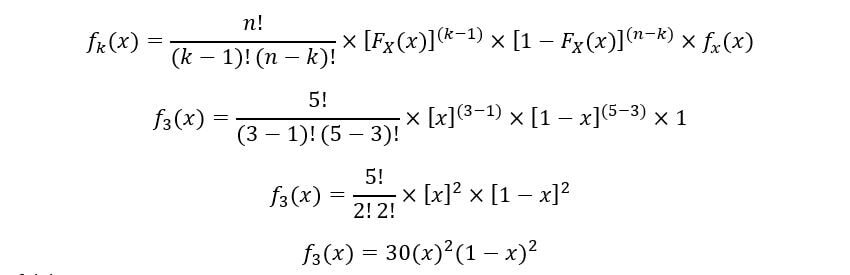
Trazar para f₅(X):

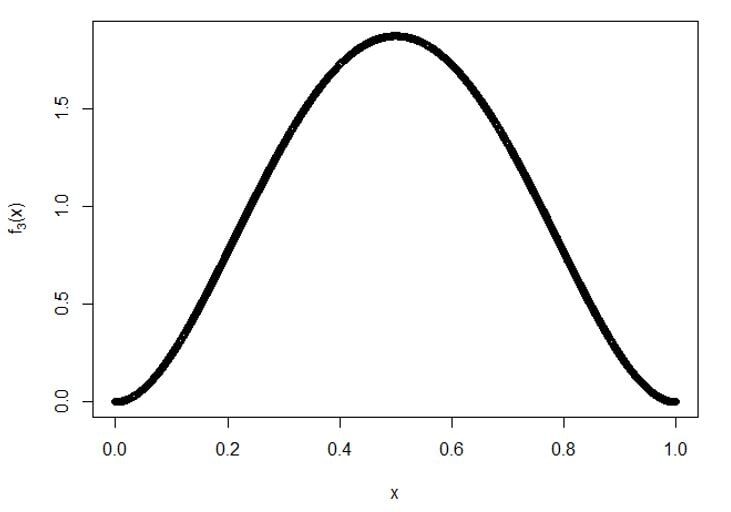
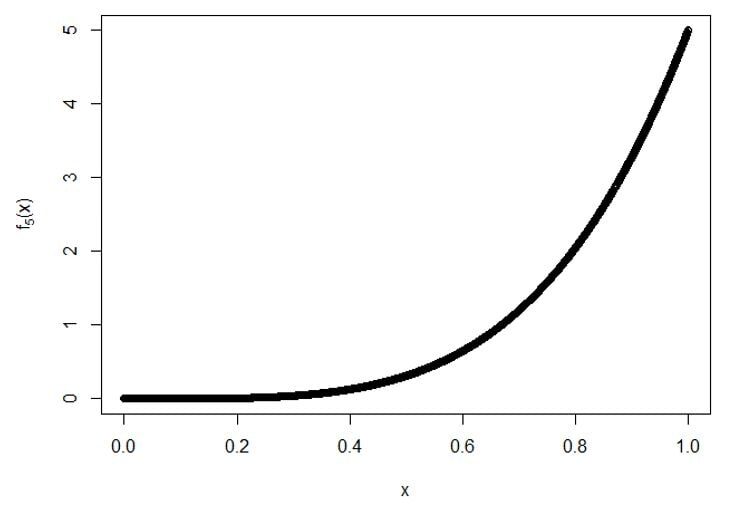
C) Para 5^th estadística de orden:

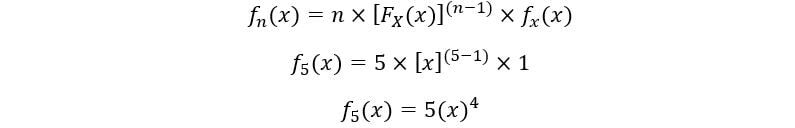
Trazar para f₅(X):

Conclusión

Por lo tanto, hemos explorado los conceptos de estadística de pedidos a fondo. Se puede modelar una amplia gama de procesos físicos a través de estadísticas de pedidos, explotando sus propiedades, particularmente sus distribuciones.

Los medios que se muestran en este artículo no son propiedad de DataPeaker y se utilizan a discreción del autor.

Relacionado