Pruebas estadísticas | Selección de características mediante pruebas estadísticas

Este artículo fue publicado como parte del Blogatón de ciencia de datos

Introducción

La selección de características es el proceso de seleccionar las características que son relevantes para un modelo de aprendizaje automático. Significa que selecciona solo aquellos atributos que tienen un efecto significativo en la salida del modelo.

Considere el caso cuando va a la tienda departamental a comprar artículos comestibles. Un producto tiene mucha información, es decir, producto, categoría, fecha de vencimiento, MRP, ingredientes y detalles de fabricación. Toda esta información son las características del producto. Normalmente, comprueba la marca, el MRP y la fecha de caducidad antes de comprar un producto. Sin embargo, la sección de ingredientes y fabricación no es de su incumbencia. Por lo tanto, la marca, el MRP, la fecha de vencimiento son características relevantes y el ingrediente, los detalles de fabricación son irrelevantes. Así es como se realiza la selección de características.

En el mundo real, un conjunto de datos puede tener miles de características y puede haber posibilidades de que algunas características sean redundantes, algunas pueden estar correlacionadas y algunas pueden ser irrelevantes para el modelo. En este escenario, si usa todas las funciones, llevará mucho tiempo entrenar el modelo y se reducirá la precisión del modelo. Por lo tanto, la selección de características se vuelve importante en la construcción de modelos. Hay muchas otras formas de selección de características, como eliminación de características recursivas, algoritmos genéticos, árboles de decisión. Sin embargo, te diré el método más básico y manual de filtrado mediante pruebas estadísticas.

Ahora que tiene un conocimiento básico de la selección de características, veremos cómo implementar varias pruebas estadísticas en los datos para seleccionar características importantes.

Objetivo

El objetivo principal de este blog es comprender las pruebas estadísticas y su implementación en datos reales en Python, lo que ayudará en la selección de características.

Terminologias

Antes de entrar en los tipos de pruebas estadísticas y su implementación, es necesario comprender los significados de algunas terminologías.

Prueba de hipótesis

La prueba de hipótesis en estadística es un método para probar los resultados de experimentos o encuestas para ver si tiene resultados significativos. Es útil cuando desea inferir sobre una población basada en una muestra o correlación entre dos o más muestras.

Hipótesis nulaLa hipótesis nula es un concepto fundamental en la estadística que establece una afirmación inicial sobre un parámetro poblacional. Su propósito es ser probada y, en caso de ser refutada, permite aceptar la hipótesis alternativa. Este enfoque es esencial en la investigación científica, ya que proporciona un marco para evaluar la evidencia empírica y tomar decisiones basadas en datos. Su formulación y análisis son cruciales en estudios estadísticos....

Esta hipótesis establece que no existe una diferencia significativa entre muestra y población o entre diferentes poblaciones. Se denota por H₀.

Ej. Suponemos que la media de 2 muestras es igual.

Hipótesis alternativa

El enunciado contrario a la hipótesis nula se incluye en la hipótesis alternativa. Se denota por H₁.

Ej. Suponemos que la media de las 2 muestras es desigual.

Valor crítico

Es un punto en la escala del estadístico de prueba más allá del cual se rechaza la hipótesis nula. Cuanto mayor sea el valor crítico, menor será la probabilidad de que 2 muestras pertenezcan a la misma distribución. El valor crítico para cualquier prueba puede

valor p

p-value significa ‘valor de probabilidad’; indica la probabilidad de que un resultado se haya producido por casualidad. Básicamente, el valor p se usa en la prueba de hipótesis para ayudarlo a respaldar o rechazar la hipótesis nula. Cuanto menor sea el valor p, más fuerte será la evidencia para rechazar la hipótesis nula.

Grado de libertad

El grado de libertad es el número de variables independientes. Este concepto se utiliza para calcular el estadístico t y el estadístico chi-cuadrado.

Puede referirse a statisticswho.com para obtener más información sobre estas terminologías.

Pruebas estadísticas

Una prueba estadística es una forma de determinar si la variableEn estadística y matemáticas, una "variable" es un símbolo que representa un valor que puede cambiar o variar. Existen diferentes tipos de variables, como las cualitativas, que describen características no numéricas, y las cuantitativas, que representan cantidades numéricas. Las variables son fundamentales en experimentos y estudios, ya que permiten analizar relaciones y patrones entre diferentes elementos, facilitando la comprensión de fenómenos complejos.... aleatoria sigue la hipótesis nula o la hipótesis alternativa. Básicamente, dice si la muestra y la población o dos o más muestras tienen diferencias significativas. Puede utilizar varias estadísticas descriptivas como media, medianaLa mediana es una medida estadística que representa el valor central de un conjunto de datos ordenados. Para calcularla, se organizan los datos de menor a mayor y se identifica el número que se encuentra en el medio. Si hay un número par de observaciones, se promedia los dos valores centrales. Este indicador es especialmente útil en distribuciones asimétricas, ya que no se ve afectado por valores extremos...., modo, rango o desviación estándar para este propósito. Sin embargo, generalmente usamos la media. La prueba estadística le da un número que luego se compara con el valor p. Si su valor es mayor que el valor p, acepta la hipótesis nula, de lo contrario, la rechaza.

El procedimiento para implementar cada prueba estadística será el siguiente:

• Calculamos el valor estadístico usando la fórmula matemática
• Luego calculamos el valor crítico usando tablas estadísticas.
• Con la ayuda del valor crítico, calculamos el valor p
• Si el valor p> 0.05 aceptamos la hipótesis nula, de lo contrario la rechazamos

Ahora que comprende la selección de características y las pruebas estadísticas, podemos avanzar hacia la implementación de varias pruebas estadísticas junto con su significado. Antes de eso, le mostraré el conjunto de datos y este conjunto de datos se utilizará para realizar todas las pruebas.

Conjunto de datos

El conjunto de datos que utilizaré es un conjunto de datos de predicción de préstamos que se tomó del concurso de análisis Vidhya. También puedes participar en el concurso y descargar el conjunto de datos. aquí.

Primero importé todos los módulos de Python necesarios y el conjunto de datos.

import numpy as np
import pandas as pd
import seaborn as sb
from numpy import sqrt, abs, round
import scipy.stats as stats
from scipy.stats import norm
df=pd.read_csv('loan.csv')
df.head()

Hay muchas características en el conjunto de datos, como género, dependientes, educación, ingresos del solicitante, monto del préstamo, historial crediticio. Usaremos estas características y verificaremos si un efecto de característica afecta a otras características usando varias pruebas, es decir, prueba Z, prueba de correlación, prueba ANOVA y prueba de Chi-cuadrado.

Prueba Z

Se utiliza una prueba Z para comparar la media de dos muestras dadas e inferir si pertenecen a la misma distribución o no. No implementamos la prueba Z cuando el tamaño de la muestra es menor a 30.

Una prueba Z puede ser una prueba Z de una muestra o una prueba Z de dos muestras.

La muestra única prueba t determina si la media muestral es estadísticamente diferente de una media poblacional conocida o hipotetizada. La prueba Z de dos muestras compara 2 variables independientes.

Implementaremos una prueba Z de dos muestras.

El estadístico Z se denota por

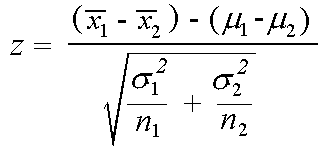
Implementación

Tenga en cuenta que implementaremos 2 pruebas z de muestra donde una variable será categórica con dos categorías y la otra variable será continua para aplicar la prueba z.

Aquí usaremos el Género variable categórica y Solicitante Ingresos variable continua. El género tiene 2 grupos: masculino y femenino. Por tanto la hipótesis será:

Hipótesis nula: No existe una diferencia significativa entre el ingreso medio de hombres y mujeres.

Hipótesis alternativa: existe una diferencia significativa entre el ingreso medio de hombres y mujeres.

Código

M_mean=df.loc[df['Gender']=='Male','ApplicantIncome'].mean()
F_mean=df.loc[df['Gender']=='Female','ApplicantIncome'].mean()
M_std=df.loc[df['Gender']=='Male','ApplicantIncome'].std()
F_std=df.loc[df['Gender']=='Female','ApplicantIncome'].std()
no_of_M=df.loc[df['Gender']=='Male','ApplicantIncome'].count()
no_of_F=df.loc[df['Gender']=='Female','ApplicantIncome'].count()

El código anterior calcula la media de los ingresos de los solicitantes masculinos, la media de los ingresos de las mujeres solicitantes, su desviación estándar y el número de muestras de hombres y mujeres.

twoSampZ La función calculará la estadística z y el valor p sin pasar por los parámetrosLos "parámetros" son variables o criterios que se utilizan para definir, medir o evaluar un fenómeno o sistema. En diversos campos como la estadística, la informática y la investigación científica, los parámetros son fundamentales para establecer normas y estándares que guían el análisis y la interpretación de datos. Su adecuada selección y manejo son cruciales para obtener resultados precisos y relevantes en cualquier estudio o proyecto.... de entrada calculados anteriormente.

def twoSampZ(X1, X2, mudiff, sd1, sd2, n1, n2):
    pooledSE = sqrt(sd1**2/n1 + sd2**2/n2)
    z = ((X1 - X2) - mudiff)/pooledSE
    pval = 2*(1 - norm.cdf(abs(z)))
    return round(z,3), pval
z,p= twoSampZ(M_mean,F_mean,0,M_std,F_std,no_of_M,no_of_F)
print('Z'= z,'p'= p)

Z = 1.828

p = 0.06759726635832197

if p<0.05:
    print("we reject null hypothesis")
else:
    print("we accept null hypothesis")

we accept the null hypothesis

Dado que el valor p es mayor que 0.5 aceptamos la hipótesis nula. Por tanto, llegamos a la conclusión de que no existe una diferencia significativa entre los ingresos de hombres y mujeres.

Prueba T

También se usa una prueba t para comparar la media de dos muestras dadas, como la prueba Z. Sin embargo, se implementa cuando el tamaño de la muestra es menor a 30. Se asume una distribución normal de la muestra. También puede ser de una o dos muestras. El grado de libertad se calcula mediante n-1 donde n es el número de muestras.

Se denota por

Implementación

Se implementará de la misma manera que la prueba Z. La única condición es que el tamaño de la muestra debe ser inferior a 30. Le he mostrado la implementación de la prueba Z. Ahora, puede probar el T-Test.

Prueba de correlación

Una prueba de correlación es una métrica para evaluar hasta qué punto las variables están asociadas entre sí.

Tenga en cuenta que las variables deben ser continuas para aplicar la prueba de correlación.

Hay varios métodos para las pruebas de correlación, es decir, covarianza, coeficiente de correlación de Pearson, coeficiente de correlación de rango de Spearman, etc.

Usaremos el coeficiente de correlación de personas ya que es independiente de los valores de las variables.

Coeficiente de correlación de Pearson

Se utiliza para medir la correlación lineal entre 2 variables. Se denota por

imagen de Google

Sus valores se encuentran entre -1 y 1.

Si el valor de r es 0, significa que no hay relación entre las variables X e Y.

Si el valor de r está entre 0 y 1, significa que hay una relación positiva entre X e Y, y su fuerza aumenta de 0 a 1. Relación positiva significa que si el valor de X aumenta, el valor de Y también aumenta.

Si el valor de r está entre -1 y 0, significa que hay una relación negativa entre X e Y, y su fuerza disminuye de -1 a 0. Relación negativa significa que si el valor de X aumenta, el valor de Y disminuye.

Implementación

Aquí usaremos dos variables o características continuas: Monto del préstamo y Ingresos del solicitante. Concluiremos si existe una relación lineal entre el monto del préstamo y los ingresos del solicitante con el valor del coeficiente de correlación de Pearson y también trazaremos el gráfico entre ellos.

Código

Hay algunos valores faltantes en la columna LoanAmount, primero, la llenamos con el valor medio. Luego calculó el valor del coeficiente de correlación.

df[‘LoanAmount’]= df[‘LoanAmount’].fillna (df[‘LoanAmount’].significar())

pcc = np.corrcoef (df.ApplicantIncome, df.LoanAmount)

imprimir (pcc)

[[1.         0.56562046]
 [0.56562046 1.        ]]

Los valores de las diagonales indican la correlación de características con ellos mismos. 0.56 representan que existe alguna correlación entre las dos características.

También podemos dibujar el gráfico de la siguiente manera:

sns.lineplot(data=df,x='LoanAmount',y='ApplicantIncome')

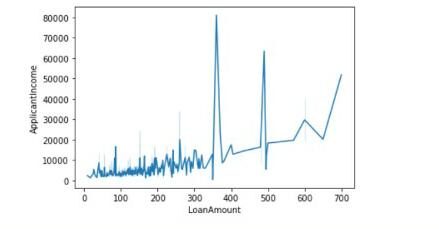
Prueba ANOVA

ANOVA significa Análisis de varianza. Como sugiere el nombre, utiliza la varianza como parámetro para comparar múltiples grupos independientes. ANOVA puede ser ANOVA unidireccional o ANOVA bidireccional. El ANOVA de una vía se aplica cuando hay tres o más grupos independientes de una variable. Implementaremos lo mismo en Python.

La estadística F se puede calcular mediante

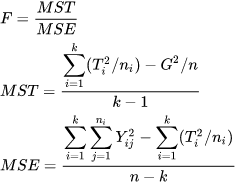
Implementación

Aquí usaremos el Dependientes variable categórica y Solicitante Ingresos variable continua. Los dependientes tiene 4 grupos: 0,1,2,3+. Por tanto la hipótesis será:

Hipótesis nula: No existe una diferencia significativa entre los ingresos medios entre los diferentes grupos de dependientes.

Hipótesis alternativa: existe una diferencia significativa entre los ingresos medios entre los diferentes grupos de dependientes.

Código

Primero, manejamos los valores faltantes en la función Dependientes.

df['Dependents'].isnull().sum()
df['Dependents']=df['Dependents'].fillna('0')

Después de esto, creamos un marco de datos con las características Dependents y ApplicantIncome. Luego, con la ayuda de la biblioteca scipy.stats, calculamos el estadístico F y el valor p.

df_anova = df[['total_bill','day']]
grps = pd.unique(df.day.values)
d_data = {grp:df_anova['total_bill'][df_anova.day == grp] for grp in grps}
F, p = stats.f_oneway(d_data['Sun'], d_data['Sat'], d_data['Thur'],d_data['Fri'])

print('F ={},p={}'.format(F,p))

F =5.955112389949444,p=0.0005260114222572804

si p <0,05:

imprimir («rechazar hipótesis nula»)

demás:

imprimir («aceptar hipótesis nula»)

Reject null hypothesis.

Dado que el valor p es menor que 0.5 rechazamos la hipótesis nula. Por tanto, concluimos que existe una diferencia significativa entre los ingresos de varios grupos de Dependientes.

Prueba de chi-cuadrado

Esta prueba se aplica cuando tiene dos variables categóricas de una población. Se utiliza para determinar si existe una asociación o relación significativa entre las dos variables.

Hay 2 tipos de pruebas de chi-cuadrado: bondad de ajuste de chi-cuadrado y prueba de chi-cuadrado para independencia, implementaremos esta última.

El grado de libertad en la prueba de chi-cuadrado se calcula mediante (n-1) * (m-1) donde nym son números de filas y columnas respectivamente.

Se denota por:

Implementación

Usaremos dos características categóricas Género y Estado del préstamo y averigüe si existe una asociación entre ellos mediante la prueba de chi-cuadrado.

Hipótesis nula: no existe una asociación significativa entre las características de género y estado del préstamo.

Hipótesis alternativa: existe una asociación significativa entre las características de género y estado del préstamo.

Código

Primero, recuperamos la columna Gender and LoanStatus y formamos una matriz.

dataset_table=pd.crosstab(dataset['sex'],dataset['smoker'])
dataset_table

Loan_Status  N  Y
Gender
Female      37   75
Male        33  339

Luego, calculamos los valores observados y esperados usando la tabla anterior.

observed=dataset_table.values
val2=stats.chi2_contingency(dataset_table)
expected=val2[3]

Luego calculamos la estadística de chi-cuadrado y el valor p usando el siguiente código:

from scipy.stats import chi2
chi_square=sum([(o-e)**2./e for o,e in zip(observed,expected)])
chi_square_statistic=chi_square[0]+chi_square[1]
p_value=1-chi2.cdf(x=chi_square_statistic,df=ddof)

print("chi-square statistic:-",chi_square_statistic)

print('Significance level: ',alpha)

print('Degree of Freedom: ',ddof)

print('p-value:',p_value)

chi-square statistic:- 0.23697508750826923
Significance level:  0.05
Degree of Freedom:  1
p-value: 0.6263994534115932

if p_value<=alpha:

    print("Reject Null Hypothesis")

else:

    print("Accept Null Hypthesis")

Accept Null Hypthesis

Dado que el valor p es mayor que 0.05, aceptamos la hipótesis nula. Concluimos que no existe una asociación significativa entre las dos características.

Resumen

Primero, hemos discutido la selección de funciones. Luego pasamos a las pruebas estadísticas y diversas terminologías relacionadas con él. Por último, hemos visto la aplicación de pruebas estadísticas, es decir, prueba Z, prueba T, prueba de correlación, prueba ANOVA y Chi-cuadrado junto con su implementación en Python.

Referencias

Imagen destacada – Imagen de Google

Estadísticas – statisticswho.com

Sobre mí

¡Hola! Soy Ashish Choudhary. Estoy estudiando B.Tech de la Universidad de Ciencia y Tecnología JC Bose. La ciencia de datos es mi pasión y me enorgullece escribir blogs interesantes relacionados con ella. No dudes en contactarme en LinkedIn.

Los medios que se muestran en este artículo no son propiedad de DataPeaker y se utilizan a discreción del autor.

Relacionado