Este artículo fue publicado como parte del Blogatón de ciencia de datos.
Introducción
Tabla de contenido
-
¿Qué es la regresión lineal?
-
Importancia de la regresión lineal en el análisis predictivo.
-
Aplicación práctica de regresión lineal utilizando R.
-
Aplicación en conjunto de datos de presión arterial y edad.
¿Qué es una regresión lineal?
El análisis de regresión lineal simple es una técnica para encontrar la asociación entre dos variables. Las dos variables involucradas son una variableEn estadística y matemáticas, una "variable" es un símbolo que representa un valor que puede cambiar o variar. Existen diferentes tipos de variables, como las cualitativas, que describen características no numéricas, y las cuantitativas, que representan cantidades numéricas. Las variables son fundamentales en experimentos y estudios, ya que permiten analizar relaciones y patrones entre diferentes elementos, facilitando la comprensión de fenómenos complejos.... dependiente que responde al cambio y la variable independiente. Tenga en cuenta que no estamos calculando la dependencia de la variable dependiente de la variable independiente, solo la asociación.
Por ejemplo, una empresa está invirtiendo una cierta cantidad de dinero en la comercialización de un producto y también ha recopilado datos de ventas a lo largo de los años mediante el análisis de la correlación en el presupuesto de marketing y los datos de ventas, podemos predecir la venta del próximo año si la empresa asigna un cierta cantidad de dinero para el departamento de marketing. La idea anterior de predicción suena mágica, pero es pura estadística. La regresión lineal consiste básicamente en ajustar una línea recta a nuestro conjunto de datos para que podamos predecir eventos futuros.
La línea de mejor ajuste sería de la forma:
Y = B0 + B1X
Donde, Y – Variable dependiente
X – Variable independiente
B0 y B1 – Parámetro de regresión
Predicción de la presión arterial mediante la edad por regresión en R
Ecuación de la línea de regresión en nuestro conjunto de datos.
BP = 98,7147 + 0,9709 Edad
Importando conjunto de datos
Importar un conjunto de datos de Edad vs Presión arterial que es un archivo CSV usando la función read.csv () en R y almacenar este conjunto de datos en un marco de datos bp.
bp <- read.csv ("bp.csv")
Crear marco de datos para predecir valores
Creación de un marco de datos que almacenará la edad de 53 años. Y este marco de datos se utilizará para predecir la presión arterial a los 53 años después de crear un modelo de regresión lineal.
p <- as.data.frame(53) colnames(p) <- "Age"
Creando un diagrama de dispersiónEl diagrama de dispersión es una herramienta gráfica utilizada en estadística para visualizar la relación entre dos variables. Consiste en un conjunto de puntos en un plano cartesiano, donde cada punto representa un par de valores correspondientes a las variables analizadas. Este tipo de gráfico permite identificar patrones, tendencias y posibles correlaciones, facilitando la interpretación de datos y la toma de decisiones basadas en la información visual presentada.... usando la biblioteca ggplot2
Tomando la ayuda de la biblioteca ggplot2 en R, podemos ver que existe una correlación entre la presión arterial y la edad, ya que podemos ver que el aumento de la edad es seguido por un aumento de la presión arterial.
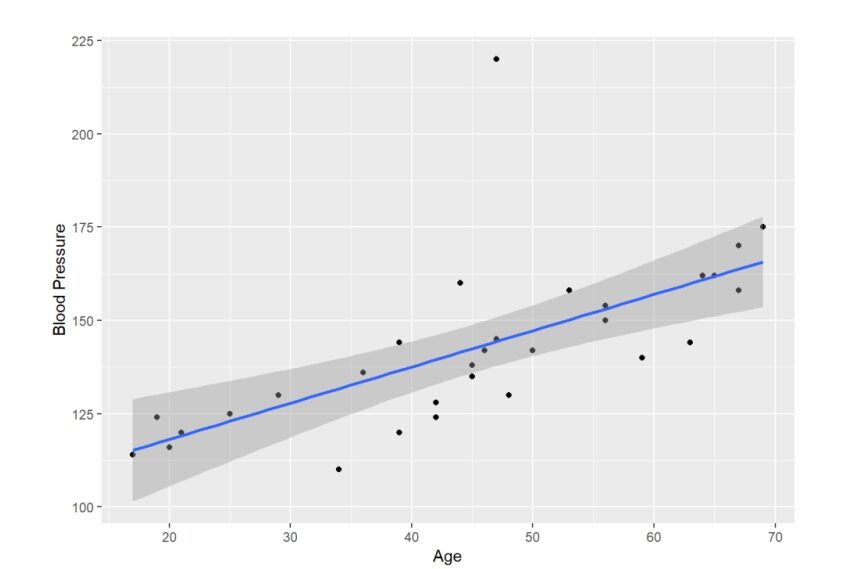
Es bastante evidente por el gráfico que la distribución en el gráfico está dispersa de tal manera que podemos ajustar una línea recta a través de los puntos.
Calcular la correlación entre la edad y la presión arterial
También podemos verificar nuestro análisis anterior de que existe una correlación entre la presión arterial y la edad tomando la ayuda de la función cor () en R que se usa para calcular la correlación entre dos variables.
cor(bp$BP,bp$Age)
[1] 0,6575673
Crear un modelo de regresión lineal
Ahora, con la ayuda de la función lm (), vamos a hacer un modelo lineal. La función lm () tiene dos atributos, primero es una fórmula donde usaremos «BP ~ Edad» porque la edad es una variable independiente y la presión arterial es una variable dependiente y el segundo son datos, donde daremos el nombre del marco de datos que contiene datos que en este caso es el marco de datos bp.
model <- lm(BP ~ Age, data = bp)
Resumen de nuestro modelo de regresión lineal
summary(model)
Producción:
## ## Call: ## lm(formula = BP ~ Age, data = bp) ## ## Residuals: ## Min 1Q Median 3Q Max ## -21.724 -6.994 -0.520 2.931 75.654 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 98.7147 10.0005 9.871 1.28e-10 *** ## Age 0.9709 0.2102 4.618 7.87e-05 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 17.31 on 28 degrees of freedom ## Multiple R-squared: 0.4324, Adjusted R-squared: 0.4121 ## F-statistic: 21.33 on 1 and 28 DF, p-value: 7.867e-05
Interpretación del modelo
## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 98.7147 10.0005 9.871 1.28e-10 *** ## Age 0.9709 0.2102 4.618 7.87e-05 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 B0 = 98.7147 (Y- intercept) B1 = 0.9709 (Age coefficient) BP = 98.7147 + 0.9709 Age
Significa que un cambio en una unidad en la edad traerá 0.9709 unidades para cambiar en la presión arterial.
El error estándar Es la variabilidad esperada en el coeficiente que captura la variabilidad del muestreo, por lo que la variación en la intersección puede ser hasta 10.0005 y la variación en la Edad será 0.2102 no más que eso
Valor T: el valor t es el coeficiente dividido por el error estándar, es básicamente qué tan grande se estima en relación con el error, mayor es el coeficiente en relación con Std. error cuanto mayor sea el puntaje t y el puntaje t viene con un valor p porque su distribución El valor p es cuán estadísticamente significativa es la variable para el modelo para un nivel de confianza del 95% compararemos este valor con alfa que será 0.05 , por lo que en nuestro caso el valor p de la intersección y la Edad es menor que alfa (alfa = 0.05), esto implica que ambos son estadísticamente significativos para nuestro modelo.
## Error estándar residual: 17.31 en 28 grados de libertad
## R cuadrado múltiple: 0,4324, R cuadrado ajustado: 0,4121
## Estadístico F: 21,33 en 1 y 28 DF, valor p: 7,867e-05
Error estándar residual o el error estándar del modelo es básicamente el error promedio para el modelo que es 17.31 en nuestro caso y significa que nuestro modelo puede tener un error promedio de 17.31 mientras predice la presión arterial. Cuanto menor sea el error, mejor será el modelo al predecir.
Múltiple R-cuadrado es la razón de (1- (suma del error al cuadrado / suma del total al cuadrado))
R cuadrado ajustado:
Si agregamos variables, no importa si es significativo en la predicción o no, el valor de R cuadrado aumentará, razón por la cual se usa R cuadrado ajustado porque si la variable agregada no es significativa para la predicción del modelo, el valor de R ajustado -squared reducirá, es una de las herramientas más útiles para evitar el sobreajuste del modelo.
F – estadísticas es la razón entre el cuadrado medio del modelo y el cuadrado medio del error, en otras palabras, es la razón de qué tan bien está funcionando el modelo y qué está haciendo el error, y cuanto mayor es el valor F, mejor es el modelo está funcionando en comparación con el error.
Uno son los grados de libertad del numerador del estadístico F y 28 es el grado de libertad de los errores.
Predecir el valor de la presión arterial a los 53 años
BP = 98,7147 + 0,9709 Edad
La fórmula anterior se usará para calcular la presión arterial a la edad de 53 años y esto se logrará usando la función de predicción () primero escribiremos el nombre del modelo de regresión lineal separándolo por una coma dando el valor del nuevo conjunto de datos en p ya que la Edad 53 se guardó anteriormente en el marco de datos p.
predict(model, newdata = p)
## 1
## 150.1708
Entonces, el valor previsto de la presión arterial es 150,17 a los 53 años.
Como hemos predicho la presión arterial con la asociación de Edad, ahora puede haber más de una variable independiente involucrada que muestra una correlación con una variable dependiente que se llama Regresión múltiple.
Modelo de regresión lineal múltiple
El análisis de regresión multilineal es una técnica estadística para encontrar la asociación de múltiples variables independientes en la variable dependiente. Por ejemplo, los ingresos generados por una empresa dependen de varios factores, incluido el tamaño del mercado, el precio, la promoción, el precio de la competencia, etc. Básicamente, el modelo de regresión lineal múltiple establece una relación lineal entre una variable dependiente y múltiples variables independientes.
La ecuación de regresión lineal múltiple es la siguiente:
Y = B0 + B1X1 + B2X2 + .. + BnXk + E
Dónde
Y – Variable dependiente
X – Variable independiente
B0, B1, B3,. – Coeficientes de regresión lineal múltiple
E- Error
Tomando otro ejemplo del conjunto de datos Wine y con la ayuda de AGST, HarvestRain vamos a predecir el precio del vino.
Importando el conjunto de datos
Usando la función read.csv (), importe el conjunto de datos wine.csv y wine_test.csv en el marco de datos wine y wine_test respectivamente.
wine <- read.csv("wine.csv")
wine_test <- read.csv("wine_test.csv")
Descargue el conjunto de datos desde abajo
Encontrar la correlación entre diferentes variables
Usando la función cor () y la función round () podemos redondear la correlación entre todas las variables del conjunto de datos wine a dos decimales.
round(cor(wine),2)
Producción:
Year Price WinterRain AGST HarvestRain Age FrancePop ## Year 1.00 -0.45 0.02 -0.25 0.03 -1.00 0.99 ## Price -0.45 1.00 0.14 0.66 -0.56 0.45 -0.47 ## WinterRain 0.02 0.14 1.00 -0.32 -0.28 -0.02 0.00 ## AGST -0.25 0.66 -0.32 1.00 -0.06 0.25 -0.26 ## HarvestRain 0.03 -0.56 -0.28 -0.06 1.00 -0.03 0.04 ## Age -1.00 0.45 -0.02 0.25 -0.03 1.00 -0.99 ## FrancePop 0.99 -0.47 0.00 -0.26 0.04 -0.99 1.00
Parcelas dispersas
Al usar la biblioteca ggplot2 en R, cree un diagrama de dispersión que pueda mostrar claramente que AGST y el precio del vino están altamente correlacionados. Del mismo modo, el gráfico de dispersiónUn gráfico de dispersión es una representación visual que muestra la relación entre dos variables numéricas mediante puntos en un plano cartesiano. Cada eje representa una variable, y la ubicación de cada punto indica su valor en relación con ambas. Este tipo de gráfico es útil para identificar patrones, correlaciones y tendencias en los datos, facilitando el análisis y la interpretación de relaciones cuantitativas.... entre HarvestRain y el precio del vino también muestra su correlación.
ggplot(wine,aes(x = AGST, y = Price)) + geom_point() +geom_smooth(method = "lm")
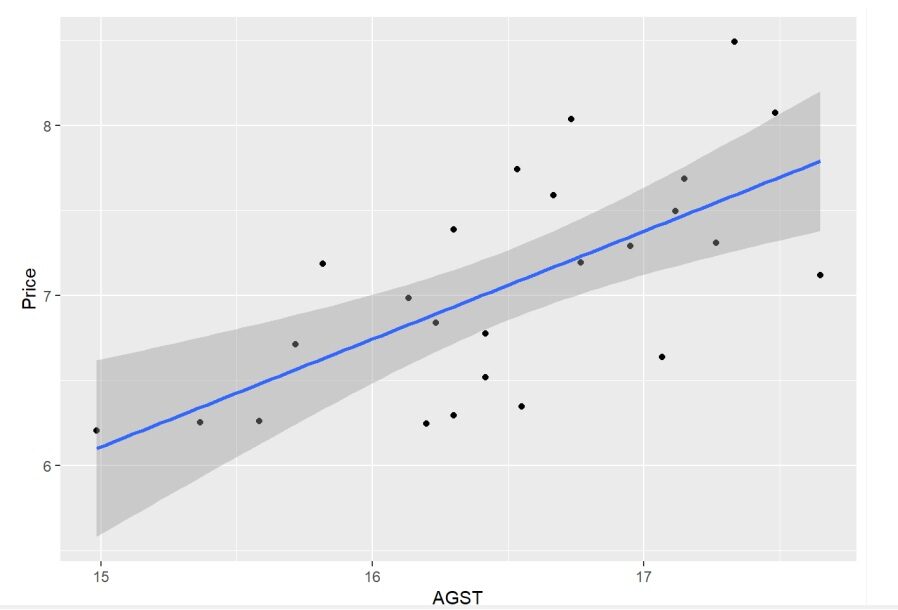
ggplot(wine,aes(x = HarvestRain, y = Price)) + geom_point() +geom_smooth(method = "lm")
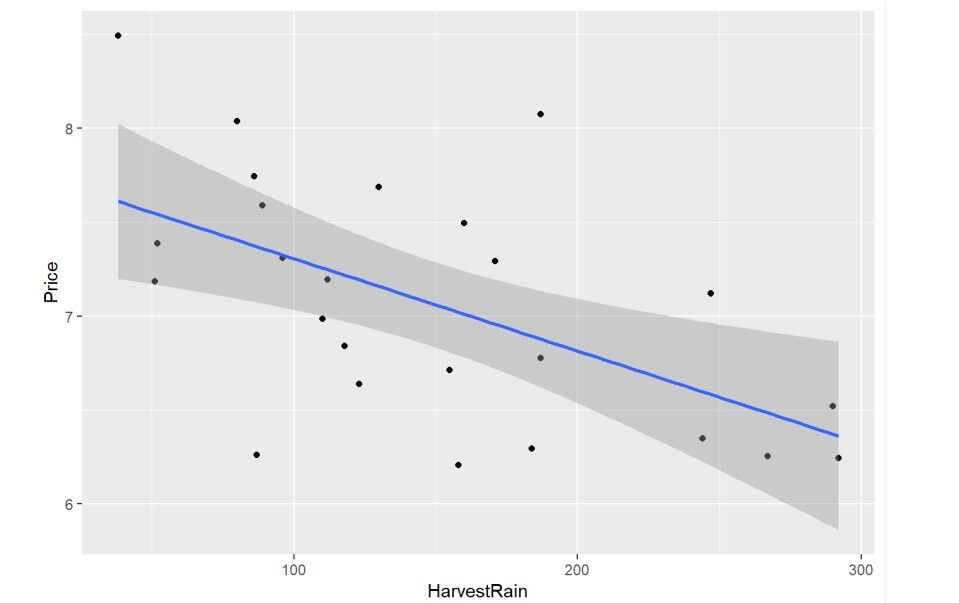
Crear un modelo de regresión multilineal
model1 <- lm(Price ~ AGST + HarvestRain,data = wine) summary(model1)
Producción:
## ## Call: ## lm(formula = Price ~ AGST + HarvestRain, data = wine) ## ## Residuals: ## Min 1Q Median 3Q Max ## -0.88321 -0.19600 0.06178 0.15379 0.59722 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) -2.20265 1.85443 -1.188 0.247585 ## AGST 0.60262 0.11128 5.415 1.94e-05 *** ## HarvestRain -0.00457 0.00101 -4.525 0.000167 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 0.3674 on 22 degrees of freedom ## Multiple R-squared: 0.7074, Adjusted R-squared: 0.6808 ## F-statistic: 26.59 on 2 and 22 DF, p-value: 1.347e-06
Interpretación del modelo
## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) -2.20265 1.85443 -1.188 0.247585 ## AGST 0.60262 0.11128 5.415 1.94e-05 *** ## HarvestRain -0.00457 0.00101 -4.525 0.000167 *** ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 B0 = 98.7147 (Y- intercept) B1 = 0.9709 (Age coefficient) Price = -2.20265 + 0.60262 AGST - 0.00457 HarvestRain
Significa que un cambio en una unidad en AGST traerá 0,60262 unidades para cambiar en precio y un cambio de unidad en HarvestRain traerá 0,00457 unidades para cambiar en precio.
El error estándar es la variabilidad esperada en el coeficiente que captura la variabilidad del muestreo, por lo que la variación en la intersección puede ser hasta 1.85443 y la variación en AGST será 0.11128 y la variación en HarvestRain es 0.00101 no más que eso
Valor T: el valor t es el coeficiente dividido por el error estándar, es básicamente qué tan grande se estima en relación con el error, mayor es el coeficiente en relación con Std. error cuanto mayor sea el puntaje t y el puntaje t viene con un valor p porque es una distribución El valor p es cuán estadísticamente significativa es la variable para el modelo para un nivel de confianza del 95% compararemos este valor con alfa que ser 0.05, por lo que en nuestro caso el valor p de la intersección, AGST y HarvestRain es menor que alfa (alfa = 0.05), esto implica que todos son estadísticamente significativos para nuestro modelo.
## Error estándar residual: 0.3674 en 22 grados de libertad
## R cuadrado múltiple: 0,7074, R cuadrado ajustado: 0,6808
## Estadístico F: 26.59 en 2 y 22 DF, valor p: 1.347e-06
Error estándar residual o el error estándar del modelo es básicamente el error promedio para el modelo que es 0.3674 en nuestro caso y significa que nuestro modelo puede tener una diferencia promedio de 0.3674 mientras predice el precio de los vinos. Cuanto menor sea el error, mejor será el modelo al predecir.
Múltiple R-cuadrado es la razón de (1- (suma del error al cuadrado / suma del total al cuadrado))
R cuadrado ajustado:
Si agregamos variables, no importa si es significativo en la predicción o no, el valor de R cuadrado aumentará, razón por la cual se usa R cuadrado ajustado porque si la variable agregada no es significativa para la predicción del modelo, el valor de R ajustado -squared reducirá, es una de las herramientas más útiles para evitar el sobreajuste del modelo.
F – estadísticas es la razón entre el cuadrado medio del modelo y el cuadrado medio del error, en otras palabras, es la razón de qué tan bien está funcionando el modelo y qué está haciendo el error, y cuanto mayor es el valor F, mejor es el modelo está funcionando en comparación con el error.
Dos son los grados de libertad del numerador del estadístico F y 22 es el grado de libertad de los errores.
Predicción de valores para nuestro conjunto de pruebas
prediction <- predict(model1, newdata = wine_test)
Valores predichos con el conjunto de datos de prueba
prueba de vino
## Year Price WinterRain AGST HarvestRain Age FrancePop ## 1 1979 6.9541 717 16.1667 122 4 54835.83 ## 2 1980 6.4979 578 16.0000 74 3 55110.24
predicción
## 1 2 ## 6.982126 7.101033
Conclusión
Como podemos ver que a partir del conjunto de datos disponible podemos crear un modelo de regresión lineal y entrenar ese modelo, si hay suficientes datos disponibles, podemos predecir con precisión nuevos eventos o, en otras palabras, resultados futuros.






