Este artículo fue publicado como parte del Blogatón de ciencia de datos.
Introducción
Los principales objetivos de la validación de un modelo incluyen la prueba de la solidez conceptual del modelo y el ajuste continuo al propósito, incluida la identificación de posibles riesgos y limitaciones. Estas pruebas deben constituir un desafío efectivo al modelo productivo existente en beneficio de su mejora, mitigación de riesgos. Los datos para este ejercicio se toman de aquí.
Marco de validación
Se realizaron las siguientes pruebas para validar los resultados del modelo:
- Variables del modelo: IV, linealidad y VIF
- 3. Ajuste del modelo: gráficos AUROC, Gini, KS y de ganancia y elevación
- 4. Pruebas de modelos: análisis de sensibilidad
- 5. Coeficiente de estabilidad: estabilidad de la señal y estabilidad del coeficiente
2.1 Verificaciones de datos
Variables dependientes
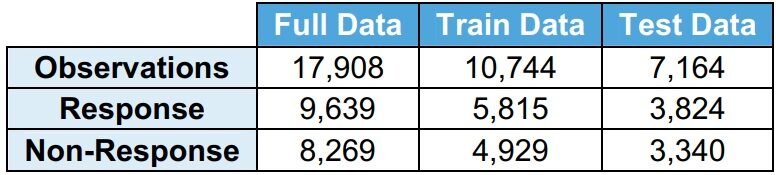
Se observa que la distribución de respuesta (Y = 1) y no respuesta (Y = 0) es muy similar entre datos completos, datos de trenes y datos de prueba.
· La respuesta (Y = 1) indica que el solicitante ha solicitado el préstamo
· Sin respuesta (Y = 0) indica que el solicitante no ha solicitado el préstamo
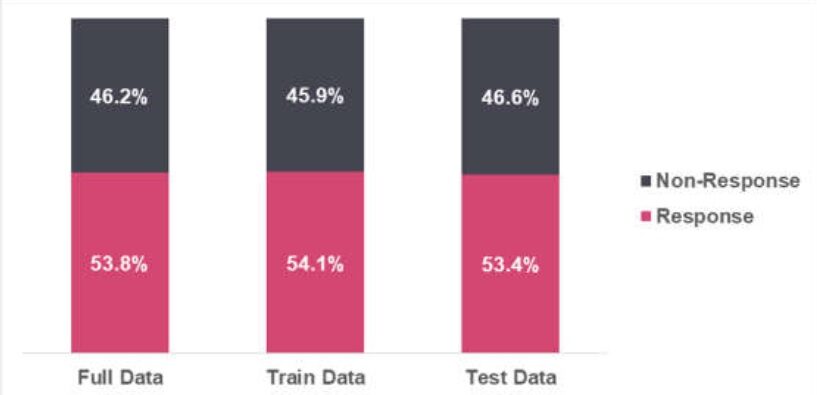
Variables independientes
Las variables independientes incluyen información personal y financiera. Las puntuaciones de riesgo se aprovechan para desarrollar el modelo. Hay 5 variables independientes en el modelo.
Se observa que no faltan valores en el conjunto de datos del tren.
Se observa que hay valores atípicos en el conjunto de datos del tren. El rango entre cuartiles (IQR = Q3 – Q1) se utiliza para identificar los puntos de venta. Los valores atípicos son valores superiores al límite superior (Q1 + 1,5 x IQR) o valores inferiores al límite inferior (Q1 – 1,5 x IQR). El equipo de validación recomienda que los valores atípicos se traten antes de desarrollar el modelo.
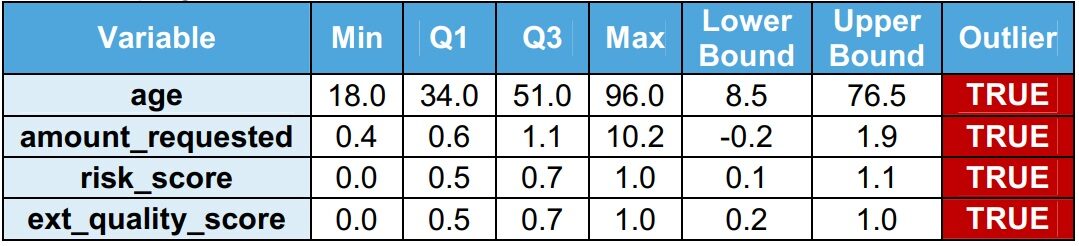
2.2. Variables del modelo
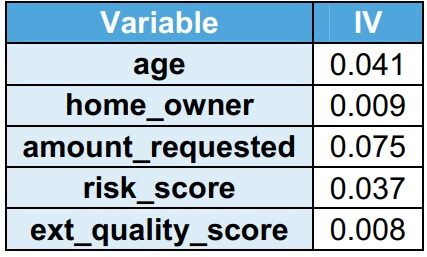
Valor de la información (IV)
from statsmodels.stats.outliers_influence import variance_inflation_factor
El poder explicativo de la variableEn estadística y matemáticas, una "variable" es un símbolo que representa un valor que puede cambiar o variar. Existen diferentes tipos de variables, como las cualitativas, que describen características no numéricas, y las cuantitativas, que representan cantidades numéricas. Las variables son fundamentales en experimentos y estudios, ya que permiten analizar relaciones y patrones entre diferentes elementos, facilitando la comprensión de fenómenos complejos.... se captura mediante IV. A medida que aumenta el poder explicativo de la variable, aumenta el IV. Se observa que todas las variables tienen IV <0.1, lo que indica que tienen un poder explicativo bajo en el conjunto de datos del tren.
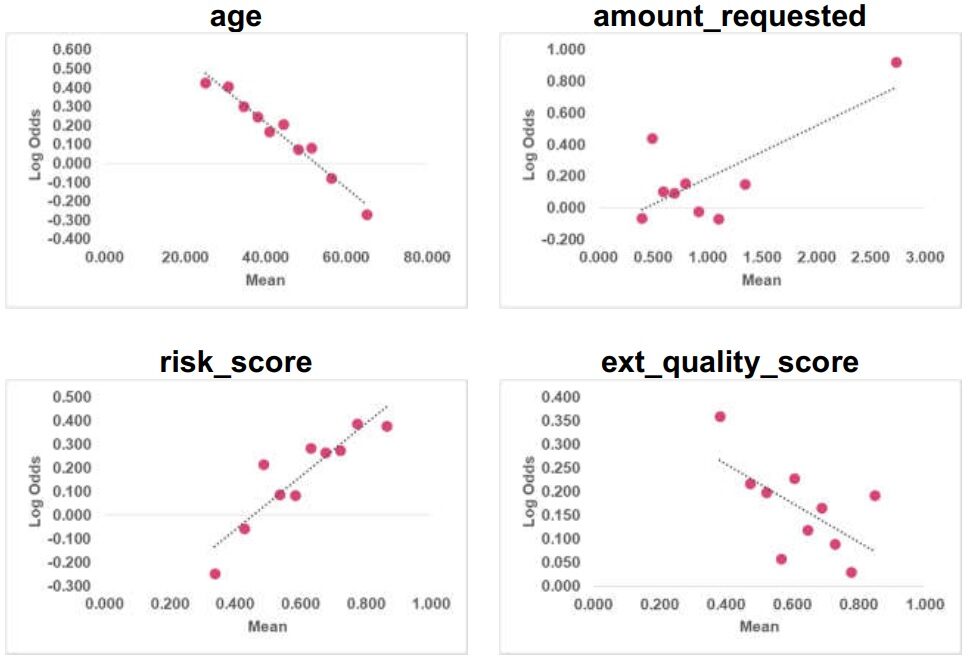
Linealidad
Paso 1: haga 10 contenedores para cada variable numérica
Paso 2: para cada intervalo, calcule la media de la variable y las probabilidades de registro correspondientes
Se comprueba la linealidad de las variables numéricas (edad, cantidad_ solicitada, puntaje_riesgo y puntaje_calidad_ ext) en los datos del tren. Se observa que age & risk_score son lineales y amount_requested & ext_quality_score no son lineales. El equipo de validación recomienda que las transformaciones se prueben para obtener una relación lineal.
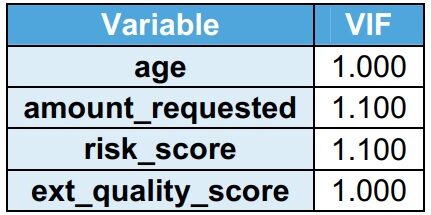
Factor de información de varianza (VIF)
VIF indica la multicolinealidad entre las variables independientes. Se observa que su VIF es menor que 2 en el conjunto de datos de entrenamientoEl entrenamiento es un proceso sistemático diseñado para mejorar habilidades, conocimientos o capacidades físicas. Se aplica en diversas áreas, como el deporte, la educación y el desarrollo profesional. Un programa de entrenamiento efectivo incluye la planificación de objetivos, la práctica regular y la evaluación del progreso. La adaptación a las necesidades individuales y la motivación son factores clave para lograr resultados exitosos y sostenibles en cualquier disciplina..... VIF menor que 2 indica que no hay multicolinealidad. Home_owner es una bandera, por lo tanto, no se considera para VIF.
2.3 Ajuste del modelo
AU-ROC
sklearn.metrics.auc(x, y)
El área bajo la Curva del operador del receptor (AUROC) se utiliza para medir el poder predictivo del modelo. AUROC = 0,50 indica que no hay poder predictivo y AUROC = 1,00 indica un poder predictivo perfecto. El modelo desarrollado con datos de trenes se ejecuta con datos de prueba y datos completos. Se observa que no existe una desviación significativa en los valores AUROC.
Se observa que AUROC es inferior a 0,6. Esto indica que el modelo no tiene un buen poder predictivo. El equipo de validación recomienda utilizar variables adicionales para mejorar el ajuste del modelo.

Gini
Fórmula: Gini = 2 x AUROC – 1
Gini se deriva de AUROC. Gini = 0.0 indica que no hay poder predictivo y Gini = 1.0 indica un poder predictivo perfecto. El modelo desarrollado con datos de trenes se ejecuta con datos de prueba y datos completos. Se observa que no existe una desviación significativa en los valores de Gini.

Kansas
scipy.stats.ks_2samp
La prueba de Kolmogorov-Smirnov (KS) mide la separación entre el% acumulativo de eventos y el% acumulativo de no eventos. Se observa que las estadísticas de las pruebas de KS son inferiores a 40, lo que indica que el modelo no es capaz de separar eventos y no eventos.

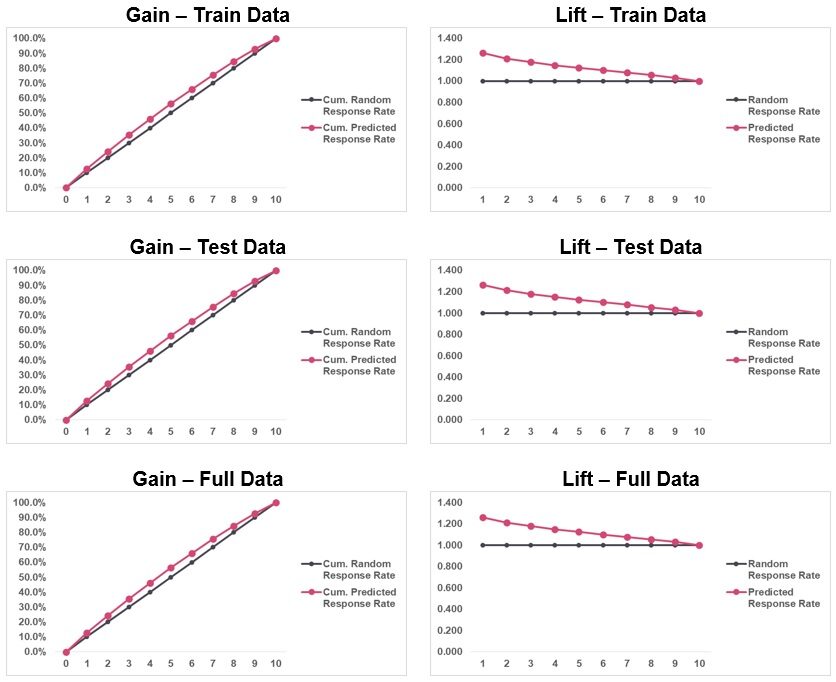
Gráficos de ganancia y elevación
Paso 1: Calcule la probabilidad de cada observación.
Paso 2: Clasifique estas probabilidades en orden decreciente.
Paso 3: Construya deciles con cada grupo teniendo casi el 10% de las observaciones.
Paso 4: Calcule la tasa de respuesta en cada decil para Bueno (respondedores), Malo (no respondedores) y total.
Los gráficos de ganancia y elevación son herramientas de visualización de datos que comparan la capacidad del clasificador para capturar la tasa de respuesta. Se observa que la tasa de respuesta acumulada prevista está muy cerca de la tasa de respuesta aleatoria acumulada. Indica que el modelo tiene un poder predictivo bajo. El equipo de validación recomienda utilizar variables adicionales para mejorar el ajuste del modelo.
2.4 Pruebas de modelos
Análisis de sensibilidad
Paso 1: normaliza todas las variables
Paso 2: ejecutar la regresión logística entre la variable dependiente y la primera
Paso 3: ejecutar la regresión logística entre la variable dependiente y la segunda
Paso 4: repita el paso anterior para el resto de las variables
Paso 5: el coeficiente de la variable indica la sensibilidad entre la variable y las probabilidades logarítmicas de la variable dependiente
Se prueba la sensibilidad del modelo con respecto a las variables numéricas independientes. La sensibilidad se comprueba en los datos del tren. El objetivo de este ejercicio es identificar las variables más sensibles. Se observa que age y risk_score son las variables más sensibles y ext_quality_score es la variable menos sensible.

2.5. Estabilidad de coeficiente
Estabilidad de coeficiente
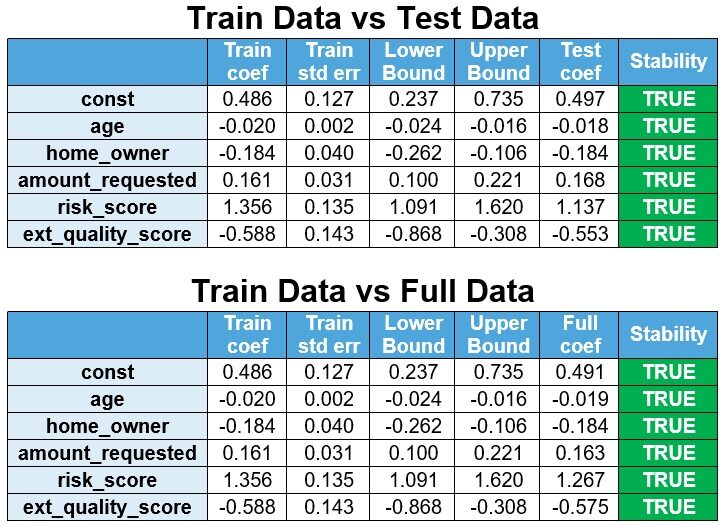
El modelo se vuelve a estimar a partir de los datos de prueba y los datos completos y los coeficientes se comparan con los datos del tren. Si los coeficientes del modelo reestimado están dentro del intervalo de confianza del 95% (Coeficiente de tren ± 1,96 x Err std de tren), entonces los coeficientes son estables.
El límite inferior se define como Coef de tren – 1,96 x Err std de tren y el límite superior se define como Coef de tren + 1,96 x Err std de tren. Se observa que los coeficientes son estables.
Estabilidad de la señal
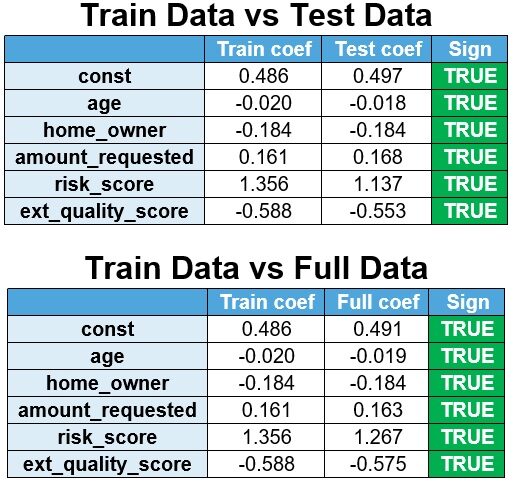
El modelo se vuelve a estimar a partir de los datos de prueba y los datos completos y los coeficientes se comparan con los datos del tren.
Se observa que los signos son estables.
Conclusión
La validación encontró que el modelo era estable. Sin embargo, se han planteado tres hallazgos de gravedad:
· Hallazgo 1 (datos de entrada) – Se observa que hay valores atípicos en el conjunto de datos del tren. El equipo de validación recomienda que los valores atípicos se traten antes de desarrollar el modelo.
· Hallando 2 (datos de entrada) – Se observa que amount_requested & ext_quality_score no son lineales. El equipo de validación recomienda que las transformaciones se prueben para obtener una relación lineal.
· Resultado 3 (ajuste del modelo) – Se observa que AUROC es bajo, Gini es bajo y KS es bajo, lo que indica que el modelo no es capaz de separar eventos y no eventos. El equipo de validación recomienda utilizar variables adicionales para mejorar el ajuste del modelo.
Los medios que se muestran en este artículo no son propiedad de DataPeaker y se utilizan a discreción del autor.






