Algoritmo de maximización de expectativas | Explicación del algoritmo EM

Este artículo fue publicado como parte del Blogatón de ciencia de datos

Introducción

son observables. Dado que no tenemos los valores para las variables no observadas (latentes), la Expectativa-Maximización El algoritmo intenta utilizar los datos existentes para determinar los valores óptimos para estas variables y luego encuentra los parámetrosLos "parámetros" son variables o criterios que se utilizan para definir, medir o evaluar un fenómeno o sistema. En diversos campos como la estadística, la informática y la investigación científica, los parámetros son fundamentales para establecer normas y estándares que guían el análisis y la interpretación de datos. Su adecuada selección y manejo son cruciales para obtener resultados precisos y relevantes en cualquier estudio o proyecto.... del modelo.

Tabla de contenido

• 👉 ¿Qué es el algoritmo de maximización de expectativas (EM)?
• 👉 Explicación detallada del algoritmo EM
• 👉 Diagrama de flujo
• 👉 Ventajas y desventajas
• 👉 Aplicaciones del algoritmo EM
• 👉 Caso de uso del algoritmo EM
  • Introducción a las distribuciones gaussianas
  • Modelos de mezcla gaussiana (GMM)
• 👉 Implementación de modelos de mezcla gaussiana en Python

¿Qué es el algoritmo de maximización de expectativas (EM)?

👉 Es un modelo de variableEn estadística y matemáticas, una "variable" es un símbolo que representa un valor que puede cambiar o variar. Existen diferentes tipos de variables, como las cualitativas, que describen características no numéricas, y las cuantitativas, que representan cantidades numéricas. Las variables son fundamentales en experimentos y estudios, ya que permiten analizar relaciones y patrones entre diferentes elementos, facilitando la comprensión de fenómenos complejos.... latente.

Primero, entendamos qué se entiende por modelo de variable latente.

Un modelo de variable latente consta de observable variables junto con inobservable variables. Las variables observadas son aquellas variables en el conjunto de datos que se pueden medir, mientras que las variables no observadas (latentes / ocultas) se infieren de las variables observadas.

• 👉 Se puede utilizar para encontrar máxima verosimilitud local (MLE) parámetros o máximo a posteriori (MAP) parámetros para variables latentes
  en un modelo estadístico o matemático.
• 👉 Se utiliza para predecir estos valores perdidos en el conjunto de datos, siempre que conozcamos la forma general de distribución de probabilidad asociada con estas variables latentes.
• 👉 En palabras simples, la idea básica detrás de este algoritmo es utilizar las muestras observables de variables latentes para predecir los valores de muestras que no son observables para el aprendizaje. Este proceso se repite hasta que se produce la convergencia de los valores.

Explicación detallada del algoritmo EM

👉 Aquí está el algoritmo que debe seguir:

• Dado un conjunto de datos incompletos, comience con un conjunto de parámetros inicializados.
• Paso de expectativa (paso E): En este paso de expectativa, utilizando los datos disponibles observados del conjunto de datos, podemos intentar estimar o adivinar los valores de los datos faltantes. Finalmente, después de este paso, obtenemos datos completos sin valores perdidos.
• Paso de maximización (paso M): Ahora, tenemos que usar los datos completos, que se preparan en el paso de expectativa, y actualizar los parámetros.
• Repita el paso 2 y el paso 3 hasta que converjamos a nuestra solución.

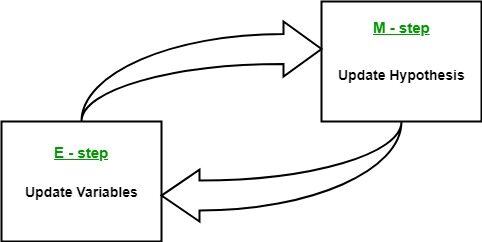
Fuente de imagen: Enlace

👉

Objetivo del algoritmo de maximización de expectativas

El algoritmo de expectativa-maximización tiene como objetivo usar los datos observados disponibles del conjunto de datos para estimar los datos faltantes de las variables latentes y luego usar esos datos para actualizar los valores de los parámetros en el paso de maximización.

Entendamos el algoritmo EM de manera detallada:

• IPaso de inicialización: En este paso, inicializamos los valores de los parámetros con un conjunto de valores iniciales, luego entregamos el conjunto de datos observados incompletos al sistema con el supuesto de que los datos observados provienen de un modelo específico. es decir, distribución de probabilidad.
• Paso de expectativa: En este paso, utilice los datos observados para estimar o adivinar los valores de los datos faltantes o incompletos. Se utiliza para actualizar las variables.
• Paso de maximización: En este paso, utilizamos los datos completos generados en el «Expectativa» paso para actualizar los valores de los parámetros, es decir, actualizar la hipótesis.
• Comprobación de la convergencia Paso: Ahora, en este paso, verificamos si los valores están convergiendo o no, si es así, deténgase, de lo contrario repita estos dos pasos, es decir, el «Expectativa» paso y «Maximización» paso hasta que se produzca la convergencia.

Diagrama de flujo para el algoritmo EM

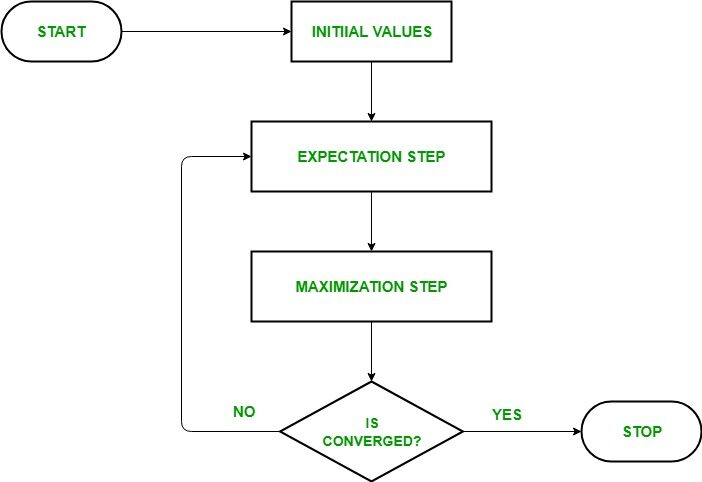
Fuente de imagen: Enlace

Ventajas y desventajas del algoritmo EM

👉 Ventajas

• Los dos pasos básicos del algoritmo EM, es decir, E-step y M-step, suelen ser bastante fáciles para muchos de los problemas de aprendizaje automático en términos de implementación.
• La solución a los pasos M a menudo existe en forma cerrada.
• Siempre se garantiza que el valor de probabilidad aumentará después de cada iteración.

👉 Desventajas

• Tiene convergencia lenta.
• Converge a la óptimo local solamente.
• Tiene en cuenta tanto las probabilidades de avance como de retroceso. Esto contrasta con la optimización numérica que considera solo probabilidades de avance.

Aplicaciones del algoritmo EM

El modelo de variable latente tiene varias aplicaciones de la vida real en el aprendizaje automático:

• 👉 Se utiliza para calcular el Densidad gaussiana de una función.
• 👉 Útil para completar el datos perdidos durante una muestra.
• 👉 Encuentra mucho uso en diferentes dominios como Procesamiento del lenguaje natural (NLP), Visión por computador, etc.
• 👉 Se utiliza en la reconstrucción de imágenes en el campo de Medicina e ingeniería estructural.
• 👉 Se utiliza para estimar los parámetros del Modelo de Markov oculto (HMM) y también para algunos otros modelos mixtos como Mezcla gaussiana Modelosetc.
• 👉 Se utiliza para encontrar los valores de variables latentes.

Caso de uso del algoritmo EM

Conceptos básicos de la distribución gaussiana

Estoy seguro de que está familiarizado con las distribuciones gaussianas (o la distribución normal), ya que esta distribución se utiliza mucho en el campo del aprendizaje automático y las estadísticas. Tiene una curva en forma de campana, con las observaciones distribuidas simétricamente alrededor del valor medio (promedio).

La imagen dada que se muestra tiene algunas distribuciones gaussianas con diferentes valores de la media (μ) y la varianza (σ²). Recuerde que cuanto mayor sea el valor de σ (desviación estándar), mayor será la extensión a lo largo del eje.

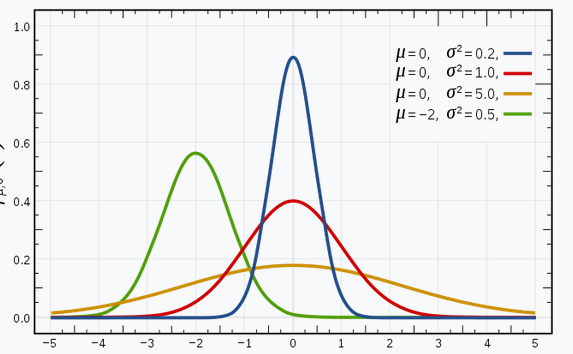
Fuente de imagen: Enlace

En el espacio 1-D, el función de densidad de probabilidad de una distribución gaussiana viene dada por:

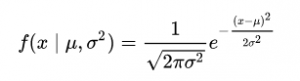
Fig. Función de densidad de probabilidad (PDF)

donde μ representa la media y σ² representa la varianza.

Pero esto solo sería cierto para una variable en 1-D únicamente. En el caso de dos variables, tendremos una curva de campana 3D en lugar de una curva en forma de campana 2D como se muestra a continuación:

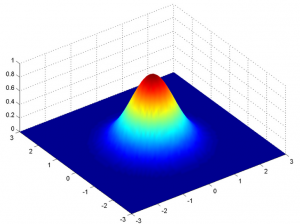
La función de densidad de probabilidad vendría dada por:

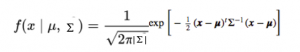
donde x es el vector de entrada, μ es el vector medio 2-D y Σ es la matriz de covarianza 2 × 2. Podemos generalizar lo mismo para la dimensión"Dimensión" es un término que se utiliza en diversas disciplinas, como la física, la matemática y la filosofía. Se refiere a la medida en la que un objeto o fenómeno puede ser analizado o descrito. En física, por ejemplo, se habla de dimensiones espaciales y temporales, mientras que en matemáticas puede referirse a la cantidad de coordenadas necesarias para representar un espacio. Su comprensión es fundamental para el estudio y... d.

Por lo tanto, para el modelo Gaussiano multivariado, tenemos xy μ como vectores de longitud d, y Σ sería un dxd Matriz de covarianza.

Por lo tanto, para un conjunto de datos que tiene D características, tendríamos una mezcla de k Distribuciones gaussianas (donde k representa el número de conglomerados), cada uno con un vector medio y una matriz de varianza determinados.

Pero nuestra pregunta es: «¿Cómo podemos averiguar la media y la varianza de cada gaussiano?»

Para encontrar estos valores, usamos una técnica llamada Expectativa-Maximización (EM).

Modelos de mezcla gaussiana

El supuesto principal de estos modelos de mezcla es que hay un cierto número de distribuciones gaussianas, y cada una de estas distribuciones representa un grupo. Por lo tanto, un modelo de mezcla gaussiana intenta agrupar las observaciones que pertenecen a una sola distribución.

Los modelos de mezcla gaussianos son modelos probabilísticos que utilizan el enfoque de agrupamientoEl "agrupamiento" es un concepto que se refiere a la organización de elementos o individuos en grupos con características o objetivos comunes. Este proceso se utiliza en diversas disciplinas, incluyendo la psicología, la educación y la biología, para facilitar el análisis y la comprensión de comportamientos o fenómenos. En el ámbito educativo, por ejemplo, el agrupamiento puede mejorar la interacción y el aprendizaje entre los estudiantes al fomentar el trabajo... suave para distribuir las observaciones en diferentes grupos, es decir, diferentes distribuciones gaussianas.

Por ejemplo, el modelo de mezcla gaussiana de 2 distribuciones gaussianas

Tenemos dos distribuciones gaussianas: N (𝜇₁, 𝜎₁²) y N(𝜇₂, 𝜎₂²)

Aquí, tenemos que estimar un total de 5 parámetros:

𝜃 = (p, 𝜇₁, 𝜎₁²,𝜇₂, 𝜎₂²)

donde p es la probabilidad de que los datos provengan de la primera distribución gaussiana y 1-p de que provengan de la segunda distribución gaussiana.

Entonces, la función de densidad de probabilidad (PDF) del modelo de mezcla viene dada por:

g (x |𝜃) = pág₁(x | 𝜇₁, 𝜎₁²) + (1-p) g₂(x | 𝜇₂, 𝜎₂² )

Objetivo: Para ajustar mejor una densidad de probabilidad dada al encontrar 𝜃 = (p, 𝜇₁, 𝜎₁², 𝜇₂, 𝜎₂²) a través de iteraciones EM.

Implementación de GMM en Python

¡Es hora de sumergirse en el código! Aquí para la implementación, usamos el Biblioteca Sklearn de Python.

Desde sklearn, usamos la clase GaussianMixture que implementa el algoritmo EM para ajustar una mezcla de modelos gaussianos. Después de la creación del objeto, utilizando el GaussianMixture.fit método podemos aprender un modelo de mezcla gaussiana a partir de los datos de entrenamientoEl entrenamiento es un proceso sistemático diseñado para mejorar habilidades, conocimientos o capacidades físicas. Se aplica en diversas áreas, como el deporte, la educación y el desarrollo profesional. Un programa de entrenamiento efectivo incluye la planificación de objetivos, la práctica regular y la evaluación del progreso. La adaptación a las necesidades individuales y la motivación son factores clave para lograr resultados exitosos y sostenibles en cualquier disciplina.....

Paso 1: Importar los paquetes necesarios

import numpy as np
import matplotlib.pyplot as plt
from sklearn.mixture import GaussianMixture

Paso 2: crea un objeto de la clase Gaussian Mixture

gmm = GaussianMixture(n_components = 2, tol=0.000001)

Paso 3: ajusta el objeto creado en el conjunto de datos dado

gmm.fit(np.expand_dims(data, 1))

Paso 4: Imprima los parámetros de 2 gaussianos de entrada

Gaussian_nr = 1
print('Input Normal_distb {:}: μ = {:.2}, σ = {:.2}'.format("1", Mean1, Standard_dev1))
print('Input Normal_distb {:}: μ = {:.2}, σ = {:.2}'.format("2", Mean2, Standard_dev2))

Output:

Input Normal_distb 1: μ = 2.0, σ = 4.0

Input Normal_distb 2: μ = 9.0, σ = 2.0

Paso 5: Imprima los parámetros después de mezclar 2 gaussianos

for mu, sd, p in zip(gmm.means_.flatten(), np.sqrt(gmm.covariances_.flatten()), gmm.weights_):
    print('Normal_distb {:}: μ = {:.2}, σ = {:.2}, weight = {:.2}'.format(Gaussian_nr, mu, sd, p))
    g_s = stats.norm(mu, sd).pdf(x) * p
    plt.plot(x, g_s, label="gaussian sklearn");
    Gaussian_nr += 1

Producción:

Normal_distb 1: μ = 1,7, σ = 3,8, peso = 0,61

Normal_distb 2: μ = 8.8, σ = 2.2, peso = 0.39

Paso 6: Trace las parcelas de distribución

sns.distplot(data, bins=20, kde=False, norm_hist=True)
gmm_sum = np.exp([gmm.score_samples(e.reshape(-1, 1)) for e in x]) 
plt.plot(x, gmm_sum, label="gaussian mixture");
plt.legend();

Producción:

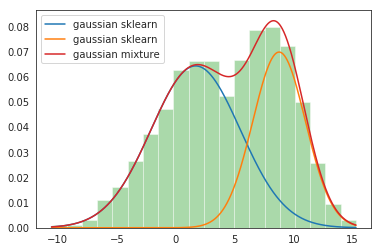
¡Esto completa nuestra implementación de GMM!

Notas finales

¡Gracias por leer!

Si le gustó esto y quiere saber más, visite mis otros artículos sobre ciencia de datos y aprendizaje automático haciendo clic en el Enlace

No dude en ponerse en contacto conmigo en Linkedin, Correo electrónico.

¿Algo no mencionado o quieres compartir tus pensamientos? No dude en comentar a continuación y me pondré en contacto con usted.

Sobre el Autor

Chirag Goyal

Actualmente, estoy cursando mi Licenciatura en Tecnología (B.Tech) en Ciencias de la Computación e Ingeniería de la Instituto Indio de Tecnología de Jodhpur (IITJ). Estoy muy entusiasmado con el aprendizaje automático, el aprendizaje profundoEl aprendizaje profundo, una subdisciplina de la inteligencia artificial, se basa en redes neuronales artificiales para analizar y procesar grandes volúmenes de datos. Esta técnica permite a las máquinas aprender patrones y realizar tareas complejas, como el reconocimiento de voz y la visión por computadora. Su capacidad para mejorar continuamente a medida que se le proporcionan más datos la convierte en una herramienta clave en diversas industrias, desde la salud... y la inteligencia artificial.

Los medios que se muestran en este artículo sobre Algoritmo de maximización de expectativas no son propiedad de DataPeaker y se utilizan a discreción del autor.

Relacionado