Visión general
- Comprender el concepto de R cuadrado y R cuadrado ajustado
- Conozca las diferencias clave entre R-cuadrado y R-cuadrado ajustado
Introducción
Cuando comencé mi viaje en la ciencia de datos, el primer algoritmo que exploré fue la regresión lineal. Después de comprender los conceptos de regresión lineal y cómo funciona el algoritmo, estaba realmente emocionado de usarlo y hacer predicciones sobre el enunciado de un problema. Estoy seguro de que la mayoría de ustedes habrían hecho lo mismo. Pero una vez que hemos predicho los valores, ¿qué sigue?
Luego viene la parte complicada. Una vez que hemos construido nuestro modelo, el siguiente paso fue evaluar su desempeño. No hace falta decir que la tarea de la evaluación del modelo es fundamental y destaca las deficiencias de nuestro modelo. Elegir el más adecuado Métrica de evaluación es una tarea crucial. Y encontré dos métricas importantes: R-cuadrado y R-cuadrado ajustado aparte de MAE / MSE / RMSE. ¿Cuál es la diferencia entre estos dos? ¿Cuál debo usar?
R cuadrado y R cuadrado ajustado son dos de estas métricas de evaluación que pueden parecer confusas para cualquier aspirante a la ciencia de datos inicialmente. Dado que ambos son extremadamente importantes para evaluar problemas de regresión, los vamos a comprender y comparar en profundidad. Ambos tienen sus pros y sus contras, que discutiremos en detalle en este artículo.
Nota: Para comprender R-cuadrado y R-cuadrado ajustado, debe tener un buen conocimiento de la regresión lineal. Consulte nuestro curso gratuito –
Tabla de contenido
- Suma residual de cuadrados
- Comprensión de la estadística R cuadrado
- Problemas con la estadística R cuadrado
- Estadístico R cuadrado ajustado
Suma residual de cuadrados
Para comprender los conceptos con claridad, abordaremos un simple problema de regresión. Aquí, estamos tratando de predecir las ‘calificaciones obtenidas’ en función de la cantidad de ‘tiempo dedicado a estudiar’. los tiempo gastado estudiando será nuestro variableEn estadística y matemáticas, una "variable" es un símbolo que representa un valor que puede cambiar o variar. Existen diferentes tipos de variables, como las cualitativas, que describen características no numéricas, y las cuantitativas, que representan cantidades numéricas. Las variables son fundamentales en experimentos y estudios, ya que permiten analizar relaciones y patrones entre diferentes elementos, facilitando la comprensión de fenómenos complejos.... independiente y el marcas logrado en la prueba es nuestro dependiente o variable de destino.
Podemos trazar un gráfico de regresión simple para visualizar estos datos.
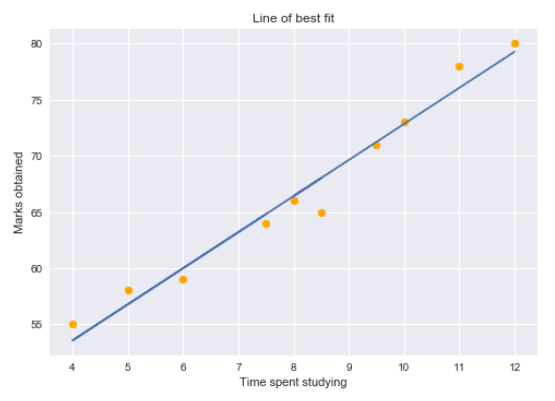
Los puntos amarillos representan los puntos de datos y la línea azul es nuestra línea de regresión predicha. Como puede ver, nuestro modelo de regresión no predice perfectamente todos los puntos de datos. Entonces, ¿cómo evaluamos las predicciones de la línea de regresión usando los datos? Bueno, podríamos comenzar determinando los valores residuales para los puntos de datos.
Residual para un punto en los datos es la diferencia entre el valor real y el valor predicho por nuestro modelo de regresión lineal.
![]()
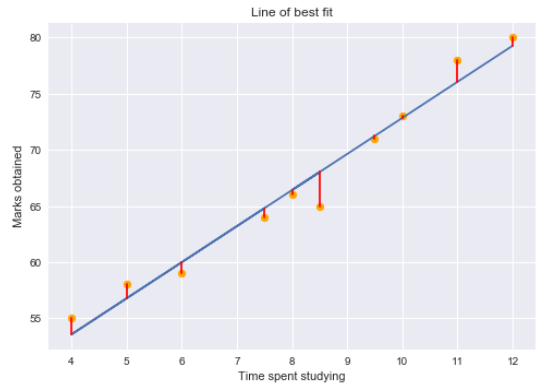
Los gráficos de residuos nos dicen si el modelo de regresión es el adecuado para los datos o no. En realidad, es una suposición del modelo de regresión que no hay tendencia en los gráficos de residuos. Para estudiar los supuestos de la regresión lineal en detalle, sugiero pasar por esta gran artículo!
Usando los valores residuales, podemos determinar la suma de los cuadrados de los residuos también conocidos como Suma de cuadrados residual o RSS.
![]()
Cuanto menor sea el valor de RSS, mejores serán las predicciones del modelo. O podemos decir que una línea de regresión es una línea de mejor ajuste si minimiza el valor de RSS. Pero hay una falla en esto: RSS es una estadística de variante de escala. Dado que RSS es la suma de la diferencia al cuadrado entre el valor real y el predicho, el valor depende de la escala de la variable objetivo.
Ejemplo:
Considere que su variable objetivo son los ingresos generados por la venta de un producto. Los residuos dependerían de la escala de este objetivo. Si la escala de ingresos se toma en «Cientos de rupias» (es decir, el objetivo sería 1, 2, 3, etc.), entonces podríamos obtener un RSS de aproximadamente 0,54 (hablando hipotéticamente).
Pero si la variable objetivo de ingresos se tomó en «rupias» (es decir, el objetivo sería 100, 200, 300, etc.), entonces podríamos obtener un RSS mayor como 5400. Aunque los datos no cambian, el valor de RSS varía. según la escala del objetivo. Esto hace que sea difícil juzgar cuál podría ser un buen valor de RSS.
Entonces, ¿podemos llegar a una mejor estadística que sea invariante en escala? Aquí es donde R-cuadrado entra en escena.
Comprensión de la estadística R-cuadrado
El estadístico R cuadrado o coeficiente de determinación es un estadístico invariante de escala que proporciona la proporción de variación en la variable objetivo explicada por el modelo de regresión lineal.
Esto puede parecer un poco complicado, así que déjame desglosarlo aquí. Para determinar la proporción de variación objetivo explicada por el modelo, primero debemos determinar lo siguiente:
-
Suma total de cuadrados
La variación total de la variable objetivo es la suma de los cuadrados de la diferencia entre los valores reales y su media.
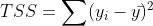
TSS o suma total de cuadrados da la variación total en Y. Podemos ver que es muy similar a la varianza de Y. Mientras que la varianza es el promedio de las sumas cuadradas de diferencia entre los valores reales y los puntos de datos, TSS es el total de las sumas al cuadrado.
Ahora que conocemos la variación total en la variable objetivo, ¿cómo determinamos la proporción de esta variación explicada por nuestro modelo? Volvemos a RSS.
-
Suma residual de cuadrados
Como comentamos antes, RSS nos da el cuadrado total de la distancia de los puntos reales desde la línea de regresión. Pero si nos enfocamos en un solo residuo, podemos decir que es la distancia que no es capturada por la línea de regresión. Por lo tanto, RSS en su conjunto nos da la variación en la variable objetivo que es no explicado por nuestro modelo.
-
Calcular R-cuadrado
Ahora, si TSS nos da la variación total en Y, y RSS nos da la variación en Y no explicada por X, entonces TSS-RSS nos da la variación en Y que se explica por nuestro modelo! Simplemente podemos dividir este valor por TSS para obtener la proporción de variación en Y que explica el modelo. Y este nuestro Estadístico R cuadrado!
R-cuadrado = (TSS-RSS) / TSS
= Variación explicada / Variación total
= 1 – Variación inexplicable / Variación total
Entonces, R cuadrado da el grado de variabilidad en la variable objetivo que se explica por el modelo o las variables independientes. Si este valor es 0,7, significa que las variables independientes explican el 70% de la variación en la variable objetivo.
El valor de R cuadrado siempre se encuentra entre 0 y 1. Un valor de R cuadrado más alto indica una mayor cantidad de variabilidad explicada por nuestro modelo y viceversa.
Si tuviéramos un valor de RSS realmente bajo, significaría que la línea de regresión estaba muy cerca de los puntos reales. Esto significa que las variables independientes explican la mayor parte de la variación en la variable objetivo. En tal caso, tendríamos un valor R cuadrado realmente alto.
Por el contrario, si tuviéramos un valor de RSS realmente alto, significaría que la línea de regresión estaría muy lejos de los puntos reales. Por lo tanto, las variables independientes no logran explicar la mayor parte de la variación en la variable objetivo. Esto nos daría un valor R cuadrado realmente bajo.
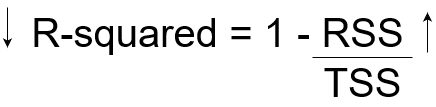
Entonces, esto explica por qué el valor R cuadrado nos da la variación en la variable objetivo dada por la variación en las variables independientes.
Problemas con la estadística R cuadrado
La estadística de R cuadrado no es perfecta. De hecho, adolece de un defecto importante. Su valor nunca disminuye sin importar el número de variables que agreguemos a nuestro modelo de regresión. Es decir, incluso si agregamos variables redundantes a los datos, el valor de R cuadrado no disminuye. O permanece igual o aumenta con la adición de nuevas variables independientes. Esto claramente no tiene sentido porque algunas de las variables independientes pueden no ser útiles para determinar la variable objetivo. R-cuadrado ajustado se ocupa de este problema.
Estadístico R cuadrado ajustado
El R-cuadrado ajustado tiene en cuenta el número de variables independientes utilizadas para predecir la variable objetivo. Al hacerlo, podemos determinar si agregar nuevas variables al modelo realmente aumenta el ajuste del modelo.
Echemos un vistazo a la fórmula de R-cuadrado ajustado para comprender mejor su funcionamiento.
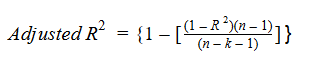
Aquí,
- norte representa la cantidad de puntos de datos en nuestro conjunto de datos
- k representa el número de variables independientes, y
- R representa los valores de R cuadrado determinados por el modelo.
Entonces, si R-cuadrado no aumenta significativamente con la adición de una nueva variable independiente, entonces el valor de R-cuadrado ajustado en realidad disminuirá.
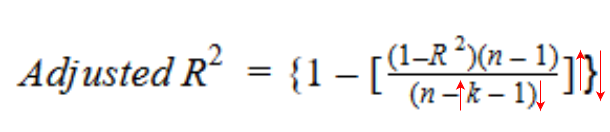
Por otro lado, si al agregar la nueva variable independiente vemos un aumento significativo en el valor de R cuadrado, entonces el valor de R cuadrado ajustado también aumentará.
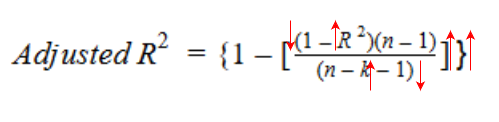
Podemos ver la diferencia entre los valores de R cuadrado y R cuadrado ajustado si agregamos una variable independiente aleatoria a nuestro modelo.

Como puede ver, agregar una variable independiente aleatoria no ayudó a explicar la variación en la variable objetivo. Nuestro valor de R cuadrado sigue siendo el mismo. Por lo tanto, nos da una indicación falsa de que esta variable podría ser útil para predecir la salida. Sin embargo, el valor de R cuadrado ajustado disminuyó, lo que indicó que esta nueva variable en realidad no está capturando la tendencia en la variable objetivo.
Claramente, es mejor usar R-cuadrado ajustado cuando hay múltiples variables en el modelo de regresión. Esto nos permitiría comparar modelos con diferentes números de variables independientes.
Notas finales
En este artículo, analizamos qué es el estadístico R cuadrado y dónde falla. También echamos un vistazo a R cuadrado ajustado.
Con suerte, esto le ha dado una mejor comprensión de las cosas. Ahora puede determinar con prudencia qué variables independientes son útiles para predecir el resultado de su problema de regresión.
Para saber más sobre otras métricas de evaluación, sugiero consultar los siguientes excelentes recursos:






