Este artículo fue publicado como parte del Blogatón de ciencia de datos.
Introducción
Un método estadístico popular y ampliamente utilizado para el pronóstico de series de tiempo es el modelo ARIMA. El suavizado exponencial y los modelos ARIMA son los dos enfoques más utilizados para la predicción de series de tiempo y proporcionan enfoques complementarios al problema. Mientras que los modelos de suavizado exponencial se basan en una descripción de la tendencia y la estacionalidad de los datos, los modelos ARIMA tienen como objetivo describir las autocorrelaciones en los datos.
Para conocer la estacionalidad, consulte este blog.
Antes de hablar del modelo ARIMA, hablemos del concepto de estacionariedad y la técnica de diferenciar series temporales.
Estacionariedad
Un dato de serie de tiempo estacionario es aquel cuyas propiedades no dependen del tiempo, por eso las series de tiempo con tendencias, o con estacionalidad, no son estacionarias. la tendencia y la estacionalidad afectarán el valor de la serie de tiempo en diferentes momentos. Por otro lado, para la estacionariedad no importa cuando la observe, debe verse muy similar en cualquier momento. En general, una serie de tiempo estacionaria no tendrá patrones predecibles a largo plazo.
ARIMA es un acrónimo de Auto-Regressive Integrated Moving Average. Es una clase de modelo que captura un conjunto de diferentes estructuras temporales estándar en datos de series de tiempo.
En este tutorial, hablaremos sobre cómo desarrollar un modelo ARIMA para el pronóstico de series de tiempo en Python.
Un modelo ARIMA es una clase de modelos estadísticos para analizar y pronosticar datos de series de tiempo. Está realmente simplificado en términos de su uso. Sin embargo, este modelo es realmente poderoso.
ARIMA son las siglas de Auto-Regressive Integrated Moving Average.
Los parámetrosLos "parámetros" son variables o criterios que se utilizan para definir, medir o evaluar un fenómeno o sistema. En diversos campos como la estadística, la informática y la investigación científica, los parámetros son fundamentales para establecer normas y estándares que guían el análisis y la interpretación de datos. Su adecuada selección y manejo son cruciales para obtener resultados precisos y relevantes en cualquier estudio o proyecto.... del modelo ARIMA se definen de la siguiente manera:
p: El número de observaciones de retraso incluidas en el modelo, también llamado orden de retraso.
d: El número de veces que se diferencian las observaciones sin procesar, también llamado grado de diferencia.
q: El tamaño de la ventana de media móvil, también llamado orden de media móvil.
Se construye un modelo de regresión lineal que incluye el número y el tipo de términos especificados, y los datos se preparan mediante un grado de diferenciación para hacerlos estacionarios, es decir, eliminar las estructuras de tendencia y estacionales que afectan negativamente al modelo de regresión.
PASOS
1. Visualice los datos de la serie temporalUna serie temporal es un conjunto de datos recogidos o medidos en momentos sucesivos, generalmente en intervalos de tiempo regulares. Este tipo de análisis permite identificar patrones, tendencias y ciclos en los datos a lo largo del tiempo. Su aplicación es amplia, abarcando áreas como la economía, la meteorología y la salud pública, facilitando la predicción y la toma de decisiones basadas en información histórica....
2. Identifique si la fecha es estacionaria
3. Trace los gráficos de correlación y correlación automática
4. Construya el modelo ARIMA o ARIMA estacional basado en los datos
Empecemos
import numpy as np import pandas as pd import matplotlib.pyplot as plt %matplotlib inline
En este tutorial, estoy usando el siguiente conjunto de datos.
df=pd.read_csv('time_series_data.csv')
df.head()
# Updating the header
df.columns=["Month","Sales"]
df.head()
df.describe()
df.set_index('Month',inplace=True)
from pylab import rcParams
rcParams['figure.figsize'] = 15, 7
df.plot()
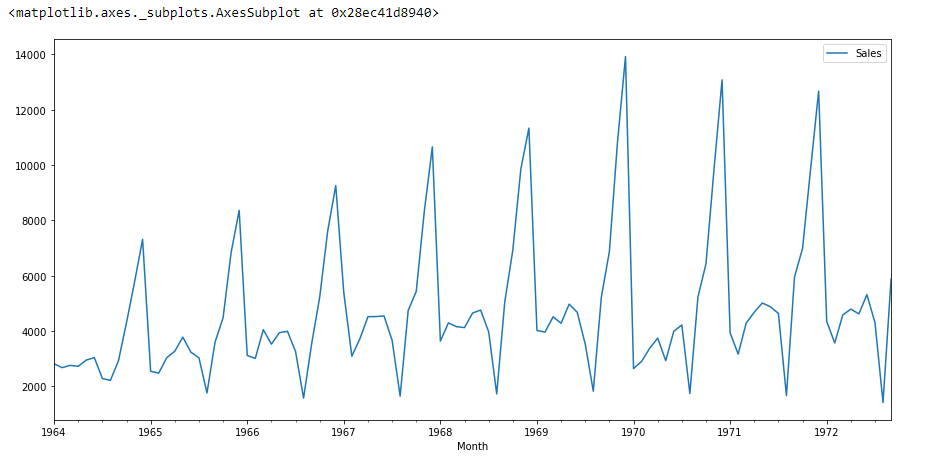
si vemos el gráfico anterior entonces podremos encontrar una tendencia de que hay un momento en que las ventas son altas y viceversa. Eso significa que podemos ver que los datos siguen la estacionalidad. Para ARIMA, lo primero que hacemos es identificar si los datos son estacionarios o no estacionarios. si los datos no son estacionarios, intentaremos hacerlos estacionarios y luego procesaremos más.
Comprobemos que si el conjunto de datos dado es estacionario o no, para eso usamos adfuller.
from statsmodels.tsa.stattools import adfuller
He importado el adfuller ejecutando el código anterior.
test_result=adfuller(df['Sales'])
Para identificar la naturaleza de los datos, usaremos la hipótesis nulaLa hipótesis nula es un concepto fundamental en la estadística que establece una afirmación inicial sobre un parámetro poblacional. Su propósito es ser probada y, en caso de ser refutada, permite aceptar la hipótesis alternativa. Este enfoque es esencial en la investigación científica, ya que proporciona un marco para evaluar la evidencia empírica y tomar decisiones basadas en datos. Su formulación y análisis son cruciales en estudios estadísticos.....
H0: La hipótesis nula: Es una declaración sobre la población que se cree que es cierta o se usa para presentar un argumento a menos que se pueda demostrar que es incorrecta más allá de una duda razonable.
H1: La hipótesis alternativa: Es una afirmación sobre la población que contradice H0 y lo que concluimos cuando rechazamos H0.
#Ho: no es estacionario
# H1: está parado
Consideraremos la hipótesis nula de que los datos no son estacionarios y la hipótesis alternativa de que los datos son estacionarios.
def adfuller_test(sales):
result=adfuller(sales)
labels = ['ADF Test Statistic','p-value','#Lags Used','Number of Observations']
for value,label in zip(result,labels):
print(label+' : '+str(value) )
if result[1] <= 0.05:
print("strong evidence against the null hypothesis(Ho), reject the null hypothesis. Data is stationary")
else:
print("weak evidence against null hypothesis,indicating it is non-stationary ")
adfuller_test(df['Sales'])
Después de ejecutar el código anterior obtendremos el valor P,
ADF Test Statistic : -1.8335930563276237 p-value : 0.3639157716602447 #Lags Used : 11 Number of Observations : 93
Aquí el valor P es 0.36, que es mayor que 0.05, lo que significa que los datos aceptan la hipótesis nula, lo que significa que los datos no son estacionarios.
Intentemos ver la primera diferencia y la diferencia estacional:
df['Sales First Difference'] = df['Sales'] - df['Sales'].shift(1) df['Seasonal First Difference']=df['Sales']-df['Sales'].shift(12) df.head()

# Again testing if data is stationary adfuller_test(df['Seasonal First Difference'].dropna())
ADF Test Statistic : -7.626619157213163 p-value : 2.060579696813685e-11 #Lags Used : 0 Number of Observations : 92
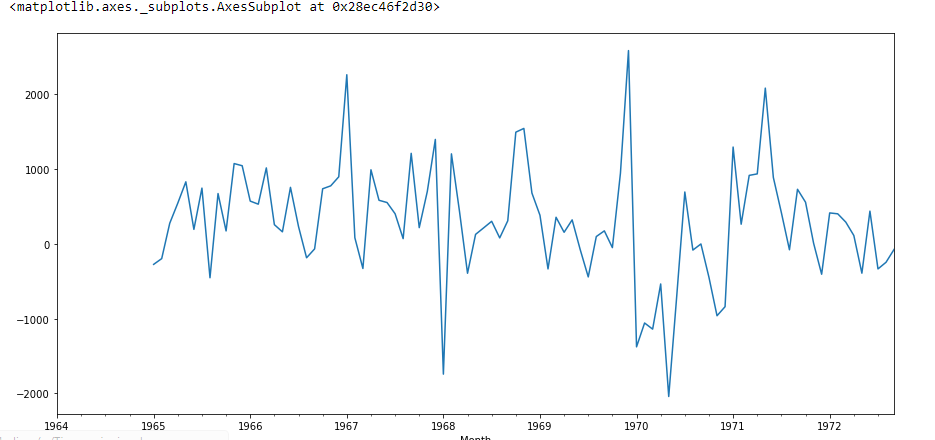
Aquí el valor P es 2.06, lo que significa que rechazaremos la hipótesis nula. Entonces los datos son estacionarios.
df['Seasonal First Difference'].plot()
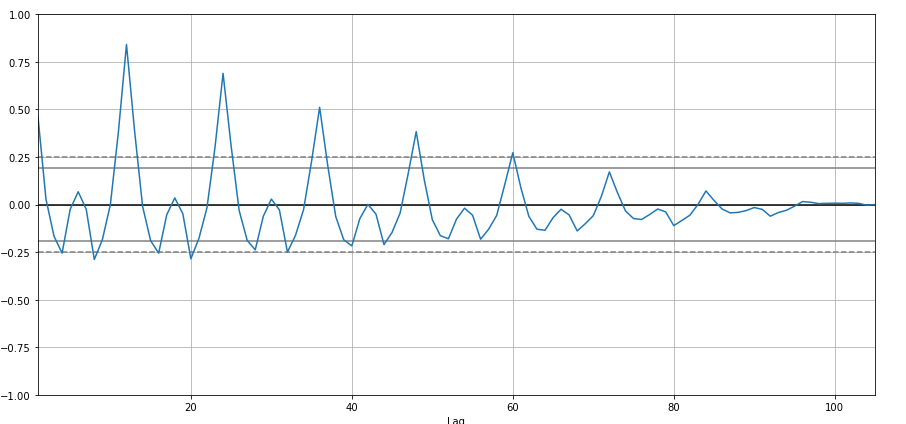
Voy a crear autocorrelación:
from pandas.plotting import autocorrelation_plot autocorrelation_plot(df['Sales']) plt.show()
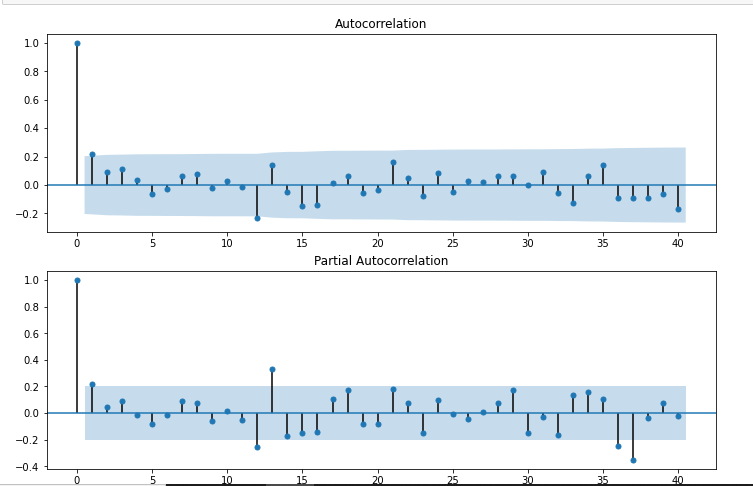
from statsmodels.graphics.tsaplots import plot_acf,plot_pacf import statsmodels.api as sm fig = plt.figure(figsize=(12,8)) ax1 = fig.add_subplot(211) fig = sm.graphics.tsa.plot_acf(df['Seasonal First Difference'].dropna(),lags=40,ax=ax1) ax2 = fig.add_subplot(212) fig = sm.graphics.tsa.plot_pacf(df['Seasonal First Difference'].dropna(),lags=40,ax=ax2)
# For non-seasonal data #p=1, d=1, q=0 or 1 from statsmodels.tsa.arima_model import ARIMA model=ARIMA(df['Sales'],order=(1,1,1)) model_fit=model.fit() model_fit.summary()
| Dep. VariableEn estadística y matemáticas, una "variable" es un símbolo que representa un valor que puede cambiar o variar. Existen diferentes tipos de variables, como las cualitativas, que describen características no numéricas, y las cuantitativas, que representan cantidades numéricas. Las variables son fundamentales en experimentos y estudios, ya que permiten analizar relaciones y patrones entre diferentes elementos, facilitando la comprensión de fenómenos complejos....: | D. Ventas | No. Observaciones: | 104 |
|---|---|---|---|
| Modelo: | ARIMA (1, 1, 1) | Probabilidad logarítmica | -951.126 |
| Método: | css-mle | SD de innovaciones | 2227.262 |
| Fecha: | Mié, 28 oct 2020 | AIC | 1910.251 |
| Tiempo: | 11:49:08 | BIC | 1920.829 |
| Muestra: | 02-01-1964 | HQIC | 1914.536 |
| – 09-01-1972 |
| coef | std err | z | P> | z | | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| constante | 22.7845 | 12.405 | 1.837 | 0.066 | -1.529 | 47.098 |
| ar.L1.D.Sales | 0.4343 | 0,089 | 4.866 | 0.000 | 0,259 | 0,609 |
| ma.L1.D.Sales | -1,0000 | 0,026 | -38.503 | 0.000 | -1.051 | -0,949 |
| Verdadero | Imaginario | Módulo | Frecuencia | |
|---|---|---|---|---|
| AR.1 | 2.3023 | + 0,0000j | 2.3023 | 0,0000 |
| MA.1 | 1,0000 | + 0,0000j | 1,0000 | 0,0000 |
df['forecast']=model_fit.predict(start=90,end=103,dynamic=True) df[['Sales','forecast']].plot(figsize=(12,8))
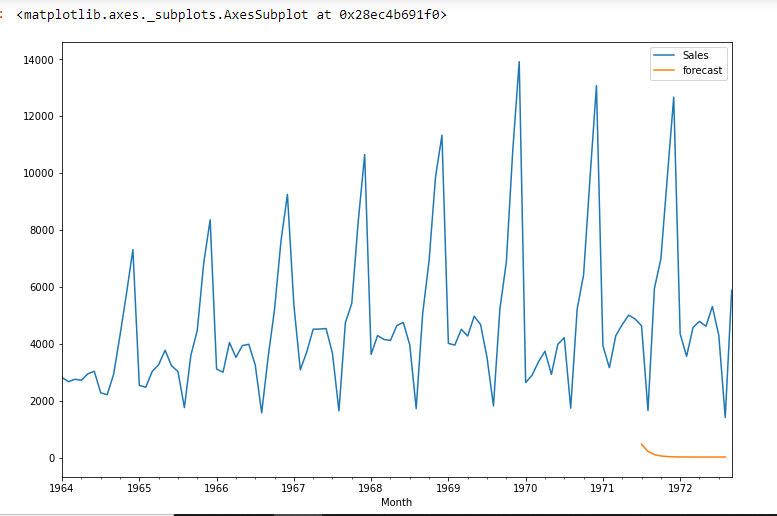
import statsmodels.api as sm model=sm.tsa.statespace.SARIMAX(df['Sales'],order=(1, 1, 1),seasonal_order=(1,1,1,12)) results=model.fit() df['forecast']=results.predict(start=90,end=103,dynamic=True) df[['Sales','forecast']].plot(figsize=(12,8))
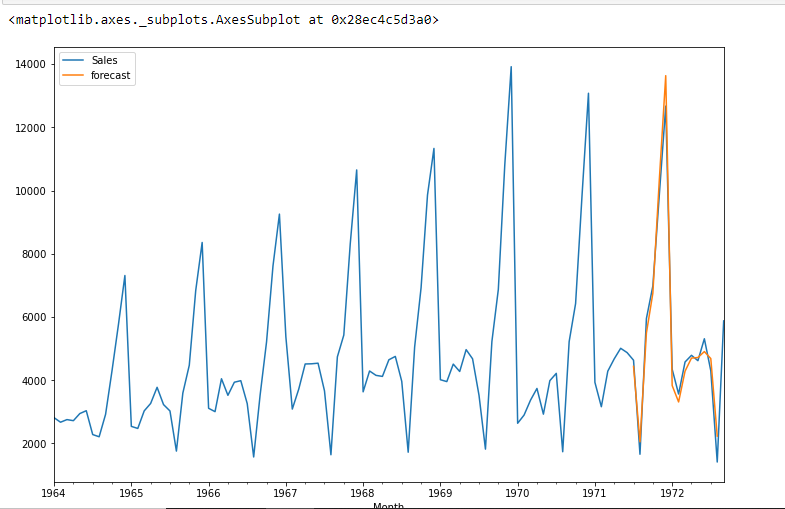
from pandas.tseries.offsets import DateOffset future_dates=[df.index[-1]+ DateOffset(months=x)for x in range(0,24)] future_datest_df=pd.DataFrame(index=future_dates[1:],columns=df.columns) future_datest_df.tail() future_df=pd.concat([df,future_datest_df]) future_df['forecast'] = results.predict(start = 104, end = 120, dynamic= True) future_df[['Sales', 'forecast']].plot(figsize=(12, 8))
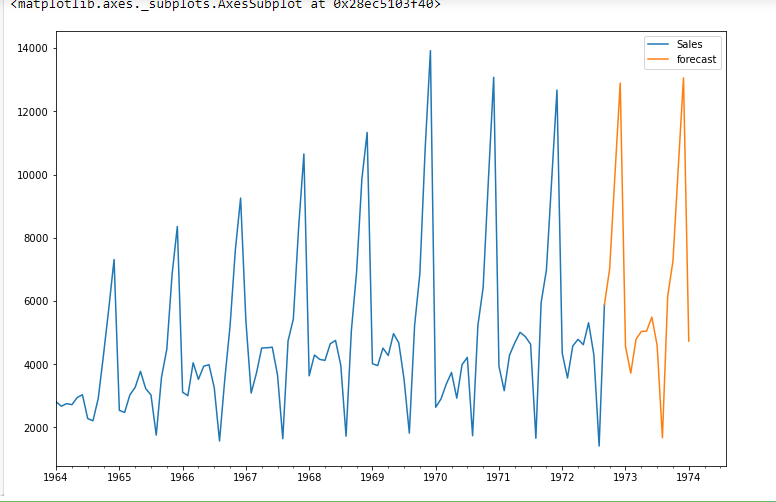
Conclusión
El pronóstico de series de tiempo es realmente útil cuando tenemos que tomar decisiones futuras o tenemos que hacer análisis, podemos hacerlo rápidamente usando ARIMA, hay muchos otros modelos de los que podemos hacer el pronóstico de series de tiempo, pero ARIMA es realmente fácil de entender.
Espero que este artículo te ayude y te ahorre una buena cantidad de tiempo. Déjame saber si tienes alguna sugerencia.
FELIZ CODIFICACIÓN.
Prabhat Pathak (Perfil de Linkedin) es analista senior.
Relacionado
Posts Relacionados:
- Métodos de predicción de series de tiempo | Arima en Python y R
- TS | Automatice el pronóstico de series de tiempo con Auto-TS
- Análisis de series de tiempo | ¿Qué es la serie temporal? Análisis de serie temporal en Python
- Spark Streaming en tiempo real | Transmisión de datos en tiempo real con Apache Spark






