Big Data

Métodos de predicción de series de tiempo | Arima en Python y R

Introducción

Imagínese esto: se le ha asignado la tarea de pronosticar el precio del próximo iPhone y se le han proporcionado datos históricos. Esto incluye características como ventas trimestrales, gastos mensuales y una gran cantidad de cosas que vienen con el balance general de Apple. Como científico de datos, ¿en qué tipo de problema clasificaría esto? Modelado de series de tiempo, por supuesto.

Desde predecir las ventas de un producto hasta estimar el uso de electricidad de los hogares, la predicción de series de tiempo es una de las habilidades centrales que se espera que cualquier científico de datos conozca, si no que domine. Hay una plétora de técnicas diferentes que puede usar, y en este artículo cubriremos una de las más efectivas, llamada Auto ARIMA.

Primero entenderemos el concepto de ARIMA que nos llevará a nuestro tema principal: Auto ARIMA. Para solidificar nuestros conceptos, tomaremos un conjunto de datos y lo implementaremos tanto en Python como en R.

Tabla de contenidos

¿Qué es una serie temporal?
Métodos para la previsión de series de tiempo
Introducción a ARIMA
Pasos para la implementación de ARIMA
¿Por qué necesitamos AutoARIMA?
Implementación automática de ARIMA (en el conjunto de datos de pasajeros aéreos)
¿Cómo selecciona los parámetros auto ARIMA?

Si está familiarizado con las series de tiempo y sus técnicas (como promedio móvil, suavizado exponencial y ARIMA), puede pasar directamente a la sección 4. Para principiantes, comience desde la sección a continuación, que es una breve introducción a las series de tiempo y varias técnicas de pronóstico. .

1. ¿Qué es una serie de tiempo?

Antes de aprender sobre las técnicas para trabajar con datos de series de tiempo, primero debemos entender qué es realmente una serie de tiempo y en qué se diferencia de cualquier otro tipo de datos. Aquí está la definición formal de serie de tiempo: es una serie de puntos de datos medido en intervalos de tiempo consistentes. Esto simplemente significa que los valores particulares se registran a un intervalo constante que puede ser por hora, diario, semanal, cada 10 días, etc. Lo que hace que las series de tiempo sean diferentes es que cada punto de datos de la serie depende de los puntos de datos anteriores. Entendamos la diferencia más claramente tomando un par de ejemplos.

Ejemplo 1:

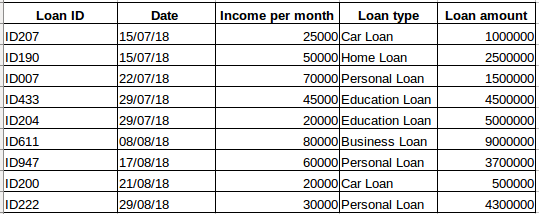
Suponga que tiene un conjunto de datos de personas que han obtenido un préstamo de una empresa en particular (como se muestra en la siguiente tabla). ¿Crees que cada fila estará relacionada con las filas anteriores? ¡Ciertamente no! El préstamo tomado por una persona se basará en sus condiciones y necesidades financieras (podría haber otros factores como el tamaño de la familia, etc., pero para simplificar estamos considerando solo los ingresos y el tipo de préstamo). Además, los datos no se recopilaron en ningún intervalo de tiempo específico. Depende de cuándo la empresa recibió una solicitud de préstamo.

Ejemplo 2:

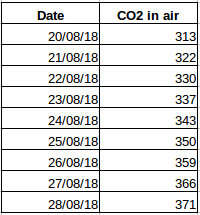
Tomemos otro ejemplo. Suponga que tiene un conjunto de datos que contiene el nivel de CO2 en el aire por día (captura de pantalla a continuación). ¿Podrá predecir la cantidad aproximada de CO2 para el día siguiente observando los valores de los últimos días? Bueno, por supuesto. Si observa, los datos se han registrado a diario, es decir, el intervalo de tiempo es constante (24 horas).

Debe haber tenido una intuición sobre esto a estas alturas: el primer caso es un problema de regresión simple y el segundo es un problema de serie de tiempo. Aunque el acertijo de las series de tiempo aquí también se puede resolver usando regresión lineal, ese no es realmente el mejor enfoque, ya que descuida la relación de los valores con todos los valores pasados relativos. Veamos ahora algunas de las técnicas comunes que se utilizan para resolver problemas de series de tiempo.

2. Métodos para la previsión de series de tiempo

Hay varios métodos para el pronóstico de series de tiempo y los cubriremos brevemente en esta sección. La explicación detallada y los códigos de Python para todas las técnicas mencionadas a continuación se pueden encontrar en este artículo: 7 técnicas para el pronóstico de series de tiempo (con códigos de Python).

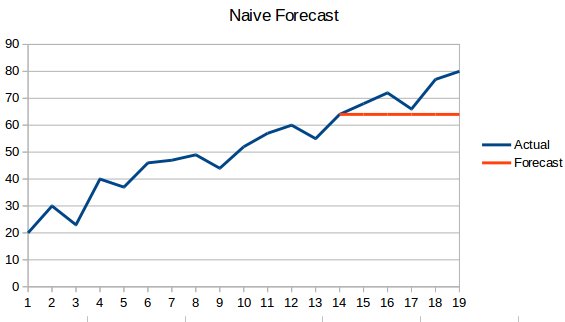
Enfoque ingenuo: En esta técnica de pronóstico, se predice que el valor del nuevo punto de datos será igual al punto de datos anterior. El resultado sería una línea plana, ya que todos los valores nuevos toman los valores anteriores.
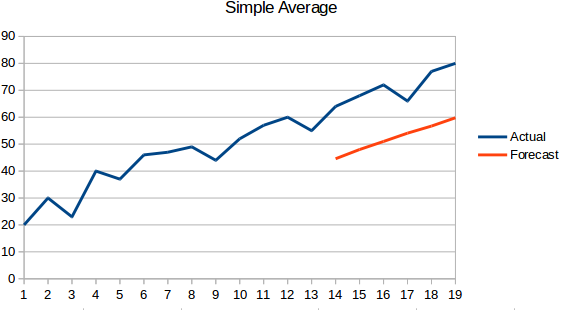
Promedio simple: El siguiente valor se toma como el promedio de todos los valores anteriores. Las predicciones aquí son mejores que el ‘Enfoque ingenuo’, ya que no resulta en una línea plana, pero aquí, todos los valores pasados se toman en consideración, lo que puede no ser siempre útil. Por ejemplo, cuando se le pida que prediga la temperatura de hoy, consideraría la temperatura de los últimos 7 días en lugar de la temperatura de hace un mes.
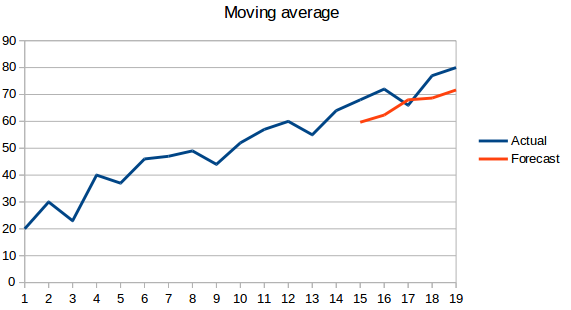
Media móvil : Esta es una mejora con respecto a la técnica anterior. En lugar de tomar el promedio de todos los puntos anteriores, el promedio de ‘n’ puntos anteriores se toma como el valor predicho.
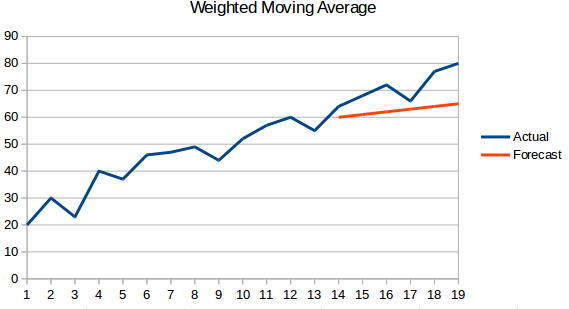
Media móvil ponderada: Una media móvil ponderada es una media móvil en la que los valores ‘n’ pasados reciben diferentes ponderaciones.
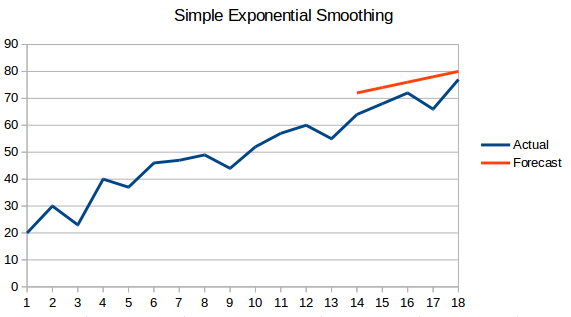
Suavizado exponencial simple: En esta técnica, se asignan mayores pesos a las observaciones más recientes que a las del pasado distante.
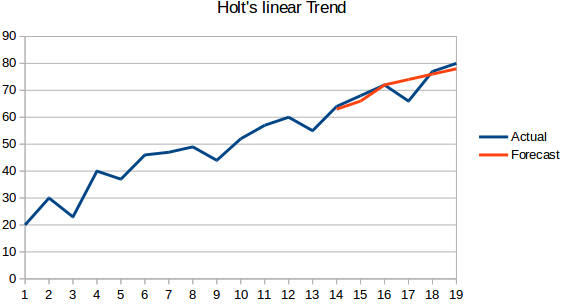
Modelo de tendencia lineal de Holt: Este método tiene en cuenta la tendencia del conjunto de datos. Por tendencia, nos referimos a la naturaleza creciente o decreciente de la serie. Supongamos que el número de reservas en un hotel aumenta cada año, entonces podemos decir que el número de reservas muestra una tendencia creciente. La función de pronóstico en este método es una función de nivel y tendencia.
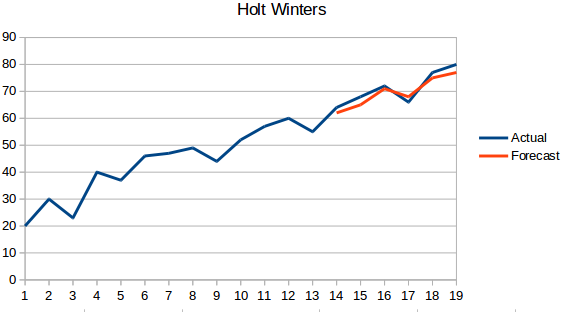
Método Holt Winters: Este algoritmo tiene en cuenta tanto la tendencia como la estacionalidad de la serie. Por ejemplo, la cantidad de reservas en un hotel es alta los fines de semana y baja los días de semana, y aumenta cada año; existe una estacionalidad semanal y una tendencia creciente.
ARIMA: ARIMA es una técnica muy popular para el modelado de series de tiempo. Describe la correlación entre los puntos de datos y tiene en cuenta la diferencia de los valores. Una mejora sobre ARIMA es SARIMA (o ARIMA estacional). Veremos ARIMA con un poco más de detalle en la siguiente sección.

3. Introducción a ARIMA

En esta sección haremos una introducción rápida a ARIMA que será útil para comprender Auto Arima. En este artículo se incluye una explicación detallada de Arima, parámetros (p, q, d), gráficos (ACF PACF) e implementación: Tutorial completo de series temporales.

ARIMA es un método estadístico muy popular para el pronóstico de series de tiempo. ARIMA significa Medias móviles integradas auto-regresivas. Los modelos ARIMA funcionan con los siguientes supuestos:

La serie de datos es estacionaria, lo que significa que la media y la varianza no deben variar con el tiempo. Una serie se puede convertir en estacionaria utilizando transformación logarítmica o diferenciando la serie.
Los datos proporcionados como entrada deben ser una serie univariante, ya que arima usa los valores pasados para predecir los valores futuros.

ARIMA tiene tres componentes: AR (término autorregresivo), I (término de diferenciación) y MA (término de promedio móvil). Entendamos cada uno de estos componentes:

El término AR se refiere a los valores pasados utilizados para pronosticar el próximo valor. El término AR está definido por el parámetro ‘p’ en arima. El valor de ‘p’ se determina utilizando el gráfico PACF.
El término MA se usa para definir el número de errores de pronóstico pasados que se usan para predecir los valores futuros. El parámetro ‘q’ en arima representa el término MA. El gráfico ACF se utiliza para identificar el valor ‘q’ correcto.
El orden de diferenciación especifica el número de veces que se realiza la operación de diferenciación en serie para hacerla estacionaria. Se pueden usar pruebas como ADF y KPSS para determinar si la serie está estacionaria y ayudar a identificar el valor d.

4. Pasos para la implementación de ARIMA

Los pasos generales para implementar un modelo ARIMA son:

Cargue los datos: El primer paso para la construcción de modelos es, por supuesto, cargar el conjunto de datos.
Preprocesamiento: Dependiendo del conjunto de datos, se definirán los pasos del preprocesamiento. Esto incluirá crear marcas de tiempo, convertir el tipo de columna de fecha / hora, hacer que la serie sea univariante, etc.
Hacer la serie estacionaria: Para satisfacer el supuesto, es necesario hacer estacionaria la serie. Esto incluiría comprobar la estacionariedad de la serie y realizar las transformaciones necesarias.
Determine el valor d: Para hacer la serie estacionaria, el número de veces que se realizó la operación de diferencia se tomará como el valor d
Cree gráficos ACF y PACF: Este es el paso más importante en la implementación de ARIMA. Los gráficos ACF PACF se utilizan para determinar los parámetros de entrada para nuestro modelo ARIMA
Determine los valores pyq: Leer los valores de pyq de las gráficas del paso anterior
Ajuste el modelo ARIMA: Utilizando los datos procesados y los valores de los parámetros que calculamos a partir de los pasos anteriores, ajuste el modelo ARIMA
Predecir valores en el conjunto de validación: Predecir los valores futuros
Calcular RMSE: Para verificar el rendimiento del modelo, verifique el valor de RMSE utilizando las predicciones y los valores reales en el conjunto de validación.

5. ¿Por qué necesitamos Auto ARIMA?

Aunque ARIMA es un modelo muy poderoso para pronosticar datos de series de tiempo, los procesos de preparación de datos y ajuste de parámetros terminan consumiendo mucho tiempo. Antes de implementar ARIMA, debe hacer que la serie sea estacionaria y determinar los valores de pyq utilizando las gráficas que discutimos anteriormente. Auto ARIMA hace que esta tarea sea realmente sencilla para nosotros, ya que elimina los pasos 3 a 6 que vimos en la sección anterior. A continuación, se muestran los pasos que debe seguir para implementar ARIMA automático:

Cargar los datos: Este paso será el mismo. Cargue los datos en su computadora portátil
Procesamiento previo de datos: la entrada debe ser univariante, por lo tanto, elimine las otras columnas
Fit Auto ARIMA: ajusta el modelo en la serie univariante
Predecir valores en el conjunto de validación: realice predicciones en el conjunto de validación
Calcular RMSE: verifique el rendimiento del modelo usando los valores predichos contra los valores reales

Pasamos por alto por completo la selección de las funciones pyq, como puede ver. ¡Qué alivio! En la siguiente sección, implementaremos auto ARIMA usando un conjunto de datos de juguete.

6. Implementación en Python y R

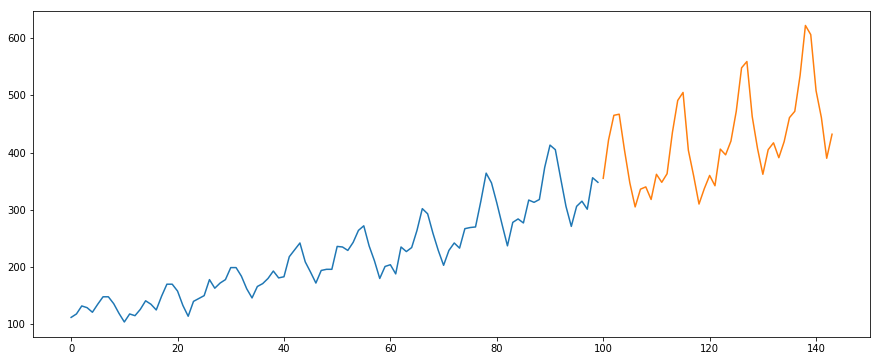
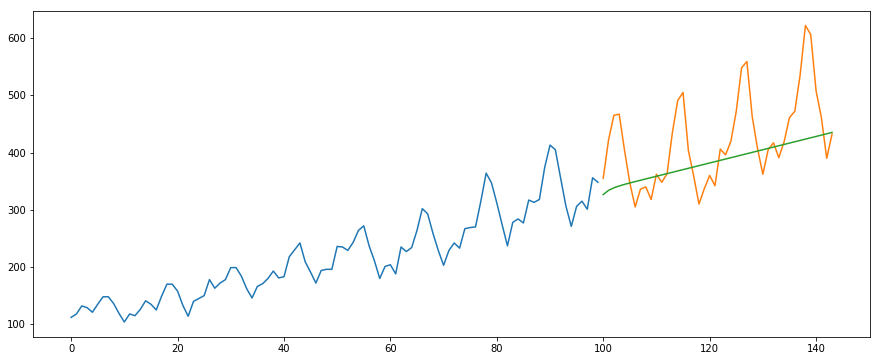
Usaremos el conjunto de datos de International-Air-Passenger. Este conjunto de datos contiene el número total mensual de pasajeros (en miles). Tiene dos columnas: mes y recuento de pasajeros. Puede descargar el conjunto de datos desde este enlace.

#load the data
data = pd.read_csv('international-airline-passengers.csv')

#divide into train and validation set
train = data[:int(0.7*(len(data)))]
valid = data[int(0.7*(len(data))):]

#preprocessing (since arima takes univariate series as input)
train.drop('Month',axis=1,inplace=True)
valid.drop('Month',axis=1,inplace=True)

#plotting the data
train['International airline passengers'].plot()
valid['International airline passengers'].plot()

#building the model
from pyramid.arima import auto_arima
model = auto_arima(train, trace=True, error_action='ignore', suppress_warnings=True)
model.fit(train)

forecast = model.predict(n_periods=len(valid))
forecast = pd.DataFrame(forecast,index = valid.index,columns=['Prediction'])

#plot the predictions for validation set
plt.plot(train, label="Train")
plt.plot(valid, label="Valid")
plt.plot(forecast, label="Prediction")
plt.show()

#calculate rmse
from math import sqrt
from sklearn.metrics import mean_squared_error

rms = sqrt(mean_squared_error(valid,forecast))
print(rms)

output -
76.51355764316357

A continuación se muestra el código R para el mismo problema:

# loading packages
library(forecast)
library(Metrics)

# reading data
data = read.csv("international-airline-passengers.csv")

# splitting data into train and valid sets
train = data[1:100,]
valid = data[101:nrow(data),]

# removing "Month" column
train$Month = NULL

# training model
model = auto.arima(train)

# model summary
summary(model)

# forecasting
forecast = predict(model,44)

# evaluation
rmse(valid$International.airline.passengers, forecast$pred)

7. ¿Cómo selecciona Auto Arima los mejores parámetros?

En el código anterior, simplemente usamos el .encajar() comando para ajustar el modelo sin tener que seleccionar la combinación de p, q, d. Pero, ¿cómo descubrió el modelo la mejor combinación de estos parámetros? Auto ARIMA tiene en cuenta los valores AIC y BIC generados (como puede ver en el código) para determinar la mejor combinación de parámetros. Los valores AIC (Akaike Information Criterion) y BIC (Bayesian Information Criterion) son estimadores para comparar modelos. Cuanto más bajos sean estos valores, mejor será el modelo.

Consulte estos enlaces si está interesado en las matemáticas detrás AIC y BIC.

8. Notas finales y lecturas adicionales

He descubierto que auto ARIMA es la técnica más simple para realizar pronósticos de series de tiempo. Conocer un atajo es bueno, pero también es importante estar familiarizado con las matemáticas detrás de él. En este artículo, he examinado los detalles de cómo funciona ARIMA, pero asegúrese de consultar los enlaces que se proporcionan en el artículo. Para su fácil referencia, aquí están los enlaces nuevamente:

Sugeriría practicar lo que hemos aprendido aquí sobre este problema de práctica: Problema de práctica de series de tiempo. También puede realizar nuestro curso de formación creado sobre el mismo problema de práctica, Pronóstico de series de tiempo, para proporcionarle una ventaja inicial.

Buena suerte y no dude en enviarnos sus comentarios y hacer preguntas en la sección de comentarios a continuación.