Regresión lineal vs logística | Regresión lineal y logística

Este artículo fue publicado como parte del Blogatón de ciencia de datos.

Introducción

Voy a discutir este tema en detalle a continuación.

Pasos de la regresión lineal

Como sugiere el nombre, la idea detrás de realizar la regresión lineal es que deberíamos llegar a una ecuación lineal que describa la relación entre las variables dependientes e independientes.

Paso 1

Supongamos que tenemos un conjunto de datos donde x es la variableEn estadística y matemáticas, una "variable" es un símbolo que representa un valor que puede cambiar o variar. Existen diferentes tipos de variables, como las cualitativas, que describen características no numéricas, y las cuantitativas, que representan cantidades numéricas. Las variables son fundamentales en experimentos y estudios, ya que permiten analizar relaciones y patrones entre diferentes elementos, facilitando la comprensión de fenómenos complejos.... independiente e Y es una función de x (Y= f (x)). Por lo tanto, al usar la regresión lineal podemos formar la siguiente ecuación (ecuación para la línea mejor ajustada):

Y = mx + c

Esta es una ecuación de una línea recta donde m es la pendiente de la línea y c es la intersección.

Paso 2

Ahora, para derivar la línea mejor ajustada, primero asignamos valores aleatorios a mycy calculamos el valor correspondiente de Y para una x dada. Este valor Y es el valor de salida.

Paso 3

Como la regresión logística es un algoritmo de aprendizaje automático supervisado, ya conocemos el valor de Y real (variable dependiente). Ahora, como tenemos nuestro valor de salida calculado (representémoslo como ŷ), podemos verificar si nuestra predicción es precisa o no.

En el caso de la regresión lineal, calculamos este error (residual) utilizando el método MSE (error cuadrático medio) y lo denominamos función de pérdidaLa función de pérdida es una herramienta fundamental en el aprendizaje automático que cuantifica la discrepancia entre las predicciones del modelo y los valores reales. Su objetivo es guiar el proceso de entrenamiento al minimizar esta diferencia, permitiendo así que el modelo aprenda de manera más efectiva. Existen diferentes tipos de funciones de pérdida, como el error cuadrático medio y la entropía cruzada, cada una adecuada para distintas tareas y...:

La función de pérdida se puede escribir como:

L = 1 / n ∑ ((y – ŷ)²)

Donde n es el número de observaciones.

Paso 4

Para lograr la línea mejor ajustada, tenemos que minimizar el valor de la función de pérdida.

Para minimizar la función de pérdida, utilizamos una técnica llamada descenso de gradienteGradiente es un término utilizado en diversos campos, como la matemática y la informática, para describir una variación continua de valores. En matemáticas, se refiere a la tasa de cambio de una función, mientras que en diseño gráfico, se aplica a la transición de colores. Este concepto es esencial para entender fenómenos como la optimización en algoritmos y la representación visual de datos, permitiendo una mejor interpretación y análisis en....

Analicemos cómo funciona el descenso de gradientes (aunque no profundizaré en los detalles, ya que este no es el tema central de este artículo).

Descenso de gradiente

Si miramos la fórmula de la función de pérdida, el ‘error cuadrático medio’ significa que el error se representa en términos de segundo orden.

Si graficamos la función de pérdida para el peso (en nuestra ecuación los pesos son myc), será una curva parabólica. Ahora que nuestra moto es minimizar la función de pérdida, tenemos que llegar al final de la curva.

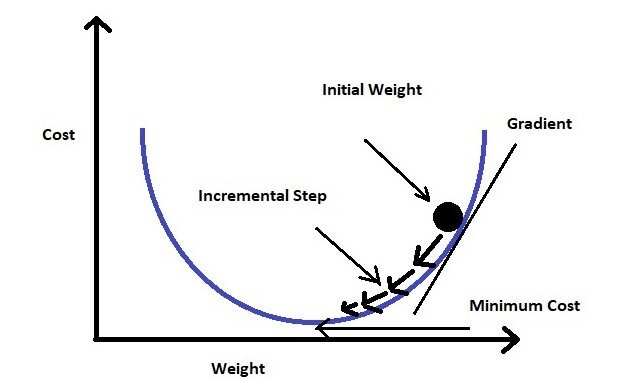
Para lograr esto, debemos tomar la derivada de primer orden de la función de pérdida para los pesos (myc). Luego restaremos el resultado de la derivada del peso inicial multiplicando por una tasa de aprendizaje (α). Seguiremos repitiendo este paso hasta alcanzar el valor mínimo (lo llamamos mínimos globales). Fijamos un umbral de un valor muy pequeño (ejemplo: 0.0001) como mínimos globales. Si no establecemos el valor de umbral, puede llevar una eternidad alcanzar el valor cero exacto.

Paso 5

Una vez que se minimiza la función de pérdida, obtenemos la ecuación final para la línea mejor ajustada y podemos predecir el valor de Y para cualquier X dado.

Aquí es donde termina la regresión lineal y estamos a solo un paso de llegar a la regresión logística.

Regresión logística

Como dije antes, fundamentalmente, la regresión logística se utiliza para clasificar elementos de un conjunto en dos grupos (clasificación binaria) calculando la probabilidad de cada elemento del conjunto.

Pasos de la regresión logística

En regresión logística, decidimos un umbral de probabilidad. Si la probabilidad de un elemento en particular es mayor que el umbral de probabilidad, clasificamos ese elemento en un grupo o viceversa.

Paso 1

Para calcular la separación binaria, primero, determinamos la línea mejor ajustada siguiendo los pasos de Regresión lineal.

Paso 2

La línea de regresión que obtenemos de la regresión lineal es muy susceptible a valores atípicos. Por lo tanto, no hará un buen trabajo al clasificar dos clases.

Por lo tanto, el valor predicho se convierte en probabilidad al alimentarlo a la función sigmoidea.

La ecuación de sigmoide:

Como podemos ver en la Fig. 3, podemos alimentar cualquier número real a la función sigmoidea y devolverá un valor entre 0 y 1.

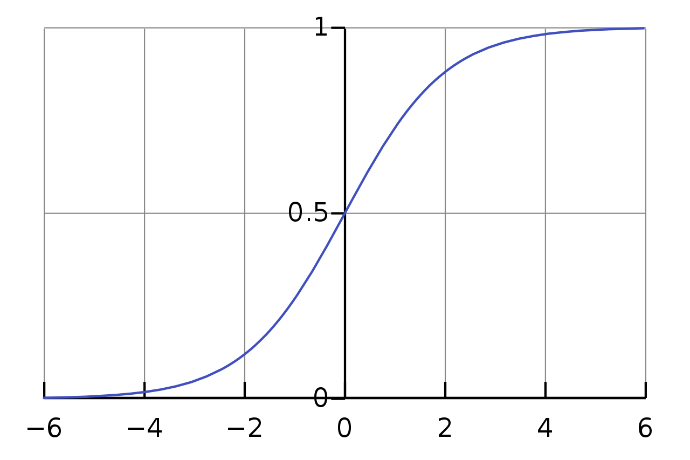
Fig 2: Curva sigmoidea (imagen tomada de Wikipedia)

Por lo tanto, si alimentamos la salida ŷ valor a la función sigmoidea vuelve a sintonizar un valor de probabilidad entre 0 y 1.

Paso 3

Finalmente, el valor de salida de la función sigmoidea se convierte en 0 o 1 (valores discretos) según el valor de umbral. Por lo general, establecemos el valor de umbral en 0,5. De esta forma, obtenemos la clasificación binaria.

Ahora que tenemos la idea básica de cómo se relacionan la regresión lineal y la regresión logística, revisemos el proceso con un ejemplo.

Ejemplo

Consideremos un problema en el que se nos proporciona un conjunto de datos que contiene la altura y el peso de un grupo de personas. Nuestra tarea es predecir el Peso para nuevas entradas en la columna Altura.

Entonces podemos descubrir que este es un problema de regresión en el que construiremos un modelo de regresión lineal. Entrenaremos el modelo con los valores de altura y peso proporcionados. Una vez que se entrena el modelo, podemos predecir el peso para un valor de altura desconocido dado.

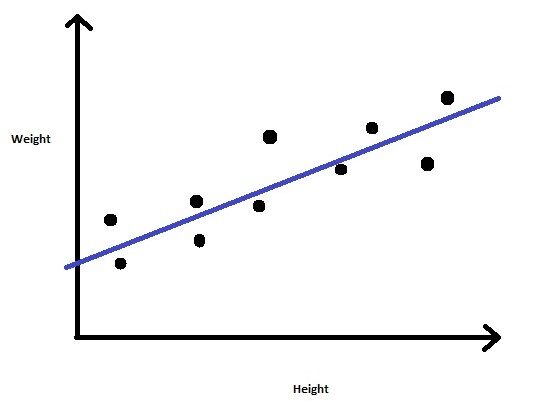
Fig 3: Regresión lineal

Ahora suponga que tenemos un campo adicional Obesidad y tenemos que clasificar si una persona es obesa o no en función de su altura y peso proporcionados. Este es claramente un problema de clasificación en el que tenemos que segregar el conjunto de datos en dos clases (obesos y no obesos).

Entonces, para el nuevo problema, podemos seguir nuevamente los pasos de Regresión lineal y construir una línea de regresión. Esta vez, la línea se basará en dos parámetrosLos "parámetros" son variables o criterios que se utilizan para definir, medir o evaluar un fenómeno o sistema. En diversos campos como la estadística, la informática y la investigación científica, los parámetros son fundamentales para establecer normas y estándares que guían el análisis y la interpretación de datos. Su adecuada selección y manejo son cruciales para obtener resultados precisos y relevantes en cualquier estudio o proyecto.... Altura y Peso y la línea de regresión se ajustará entre dos conjuntos de valores discretos. Como esta línea de regresión es muy susceptible a valores atípicos, no servirá para clasificar dos clases.

Para obtener una mejor clasificación, alimentaremos los valores de salida de la línea de regresión a la función sigmoidea. La función sigmoidea devuelve la probabilidad de cada valor de salida de la línea de regresión. Ahora, basándonos en un valor de umbral predefinido, podemos clasificar fácilmente la salida en dos clases de obesos o no obesos.

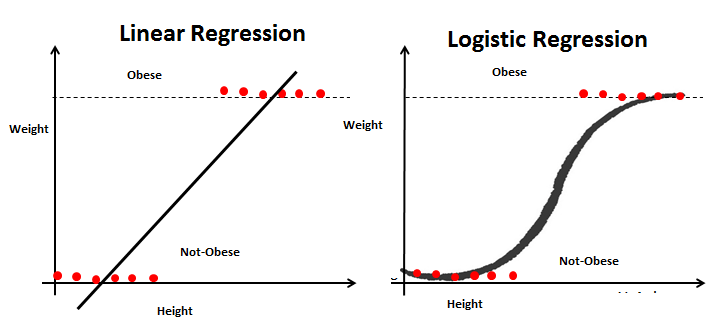
Finalmente, podemos resumir las similitudes y diferencias entre estos dos modelos.

Las similitudes entre la regresión lineal y la regresión logística

• Tanto la regresión lineal como la regresión logística son algoritmos de aprendizaje automático supervisados.
• Regresión lineal y regresión logística, ambos modelos son de regresión paramétrica, es decir, ambos modelos utilizan ecuaciones lineales para las predicciones.

Esas son todas las similitudes que tenemos entre estos dos modelos.

Sin embargo, en cuanto a funcionalidad, estos dos son completamente diferentes. A continuación se muestran las diferencias.

Las diferencias entre regresión lineal y regresión logística

• La regresión lineal se usa para manejar problemas de regresión, mientras que la regresión logística se usa para manejar los problemas de clasificación.
• La regresión lineal proporciona una salida continua, pero la regresión logística proporciona una salida discreta.
• El propósito de la regresión lineal es encontrar la línea mejor ajustada, mientras que la regresión logística está un paso por delante y ajusta los valores de la línea a la curva sigmoidea.
• El método para calcular la función de pérdida en la regresión lineal es el error cuadrático medio, mientras que para la regresión logística es la estimación de máxima verosimilitud.

Nota: Al escribir este artículo, asumí que el lector ya está familiarizado con el concepto básico de regresión lineal y regresión logística. Espero que este artículo explique la relación entre estos dos conceptos.

Relacionado