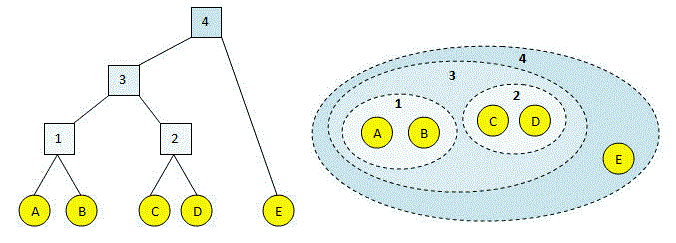
Como todos sabemos, la agrupación jerárquica aglomerativa comienza con el tratamiento de cada observación como un grupo individual y luego fusiona grupos de forma iterativa hasta que todos los puntos de datos se fusionan en un solo grupo. Los dendrogramas se utilizan para representar resultados de agrupamiento jerárquico.
Los conglomerados se fusionan en función de la distancia entre ellos y para calcular la distancia entre los conglomerados tenemos diferentes tipos de vínculos.
Criterios de vinculación:
Determina la distancia entre conjuntos de observaciones en función de la distancia por pares entre observaciones.
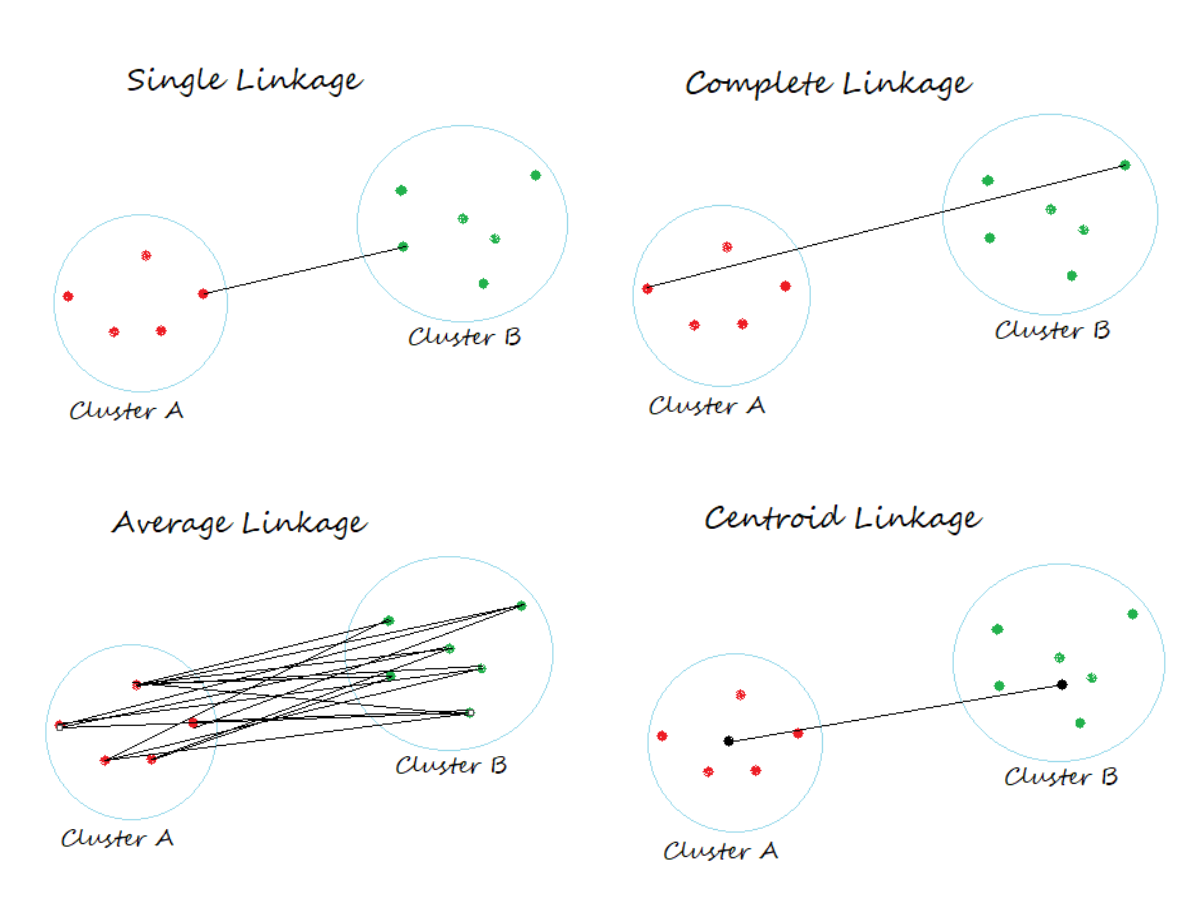
- En Enlace único, la distancia entre dos grupos es la distancia mínima entre los miembros de los dos grupos
- En Vinculación completa, la distancia entre dos grupos es la distancia máxima entre los miembros de los dos grupos
- En Vinculación promedio, la distancia entre dos conglomerados es el promedio de todas las distancias entre los miembros de los dos conglomerados
- En Enlace centroide, la distancia entre dos grupos es la distancia entre sus centroides
En este artículo, nuestro objetivo es comprender el proceso de agrupación en clústeres mediante el método de enlace único.
Agrupación mediante enlace único:
Empiece por importar las bibliotecas necesarias
import numpy as np import pandas as pd import matplotlib.pyplot as plt %matplotlib inline import scipy.cluster.hierarchy as shc from scipy.spatial.distance import squareform, pdist
Creemos datos de juguetes usando numpy.random.random_sample
a = np.random.random_sample(size = 5) b = np.random.random_sample(size = 5)
Una vez que generamos los puntos de datos aleatorios, crearemos un marco de datos de pandas.
point = ['P1','P2','P3','P4','P5']
data = pd.DataFrame({'Point':point, 'a':np.round(a,2), 'b':np.round(b,2)})
data = data.set_index('Point')
data
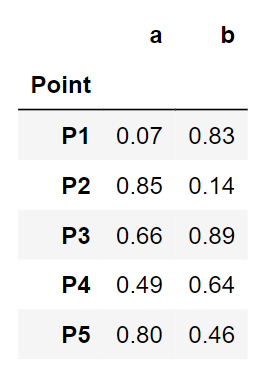
Un vistazo a los datos de nuestros juguetes. Parece limpio. Saltemos a los pasos de agrupamiento.
Paso 1: visualice los datos usando un diagrama de dispersión
plt.figure(figsize=(8,5))
plt.scatter(data['a'], data['b'], c="r", marker="*")
plt.xlabel('Column a')
plt.ylabel('column b')
plt.title('Scatter Plot of x and y')for j in data.itertuples():
plt.annotate(j.Index, (j.a, j.b), fontsize=15)
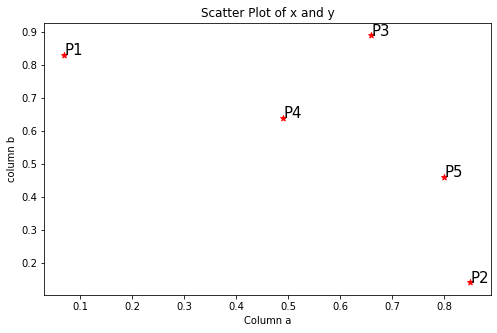
Paso 2: cálculo de la matriz de distancias en el método euclidiano usando pdist
dist = pd.DataFrame(squareform(pdist(data[[‘a’, ‘b’]]), ‘euclidean’), columns=data.index.values, index=data.index.values)
Para nuestra conveniencia, consideraremos solo los valores de límite inferior de la matriz como se muestra a continuación.
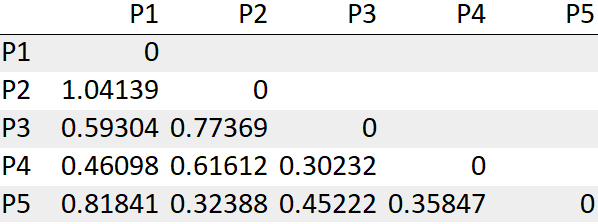
Paso 3: busque la menor distancia y combínelas en un grupo
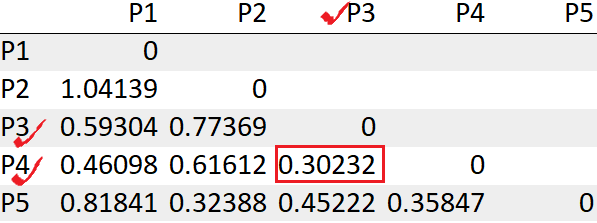
Vemos los puntos P3, P4 tiene la distancia mínima «0.30232». Entonces, primero los fusionaremos en un grupo.
Paso 4: Vuelva a calcular la matriz de distancia después de formar un grupo
Actualice la distancia entre el grupo (P3, P4) a P1
= Mín (dist (P3, P4), P1)) -> Mín (dist (P3, P1), dist (P4, P1))
= Mín (0.59304, 0.46098)
= 0,46098
Actualice la distancia entre el grupo (P3, P4) a P2
= Mín (dist (P3, P4), P2) -> Mín (dist (P3, P2), dist (P4, P2))
= Mínimo (0,77369, 0,61612)
= 0,61612
Actualice la distancia entre el grupo (P3, P4) a P5
= Mín (dist (P3, P4), P5) -> Mín (dist (P3, P5), dist (P4, P5))
= Mínimo (0.45222, 0.35847)
= 0.35847
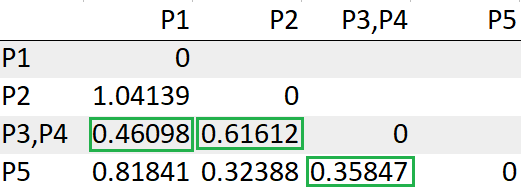
Repita los pasos 3, 4 hasta que nos quedemos con un solo grupo.
Después de volver a calcular la matriz de distancias, debemos buscar nuevamente la distancia mínima para hacer un clúster.
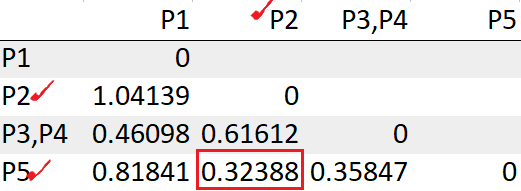
Vemos los puntos P2, P5 tiene la distancia mínima «0.32388». Así que los agruparemos en un grupo y volveremos a calcular la matriz de distancias.
Actualice la distancia entre el grupo (P2, P5) a P1
= Mín (dist ((P2, P5), P1)) -> Mín (dist (P2, P1), dist (P5, P1))
= Mín (1.04139, 0.81841)
= 0,81841
Actualice la distancia entre el grupo (P2, P5) a (P3, P4)
= Mín (dist ((P2, P5), (P3, P4))) -> = Mín (dist (P2, (P3, P4)), dist (P5, (P3, P4)))
= Mín (dist (0.61612, 0.35847))
= 0.35847
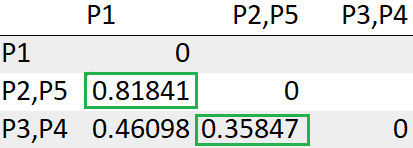
Después de volver a calcular la matriz de distancias, debemos buscar nuevamente la distancia mínima.
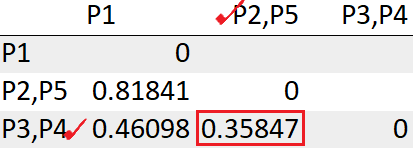
El grupo (P2, P5) tiene la menor distancia con el grupo (P3, P4) «0.35847». Entonces los agruparemos juntos.
Actualice la distancia entre el grupo (P3, P4, P2, P5) a P1
= Mín (dist (((P3, P4), (P2, P5)), P1))
= Mín (0,46098, 0,81841)
= 0,46098
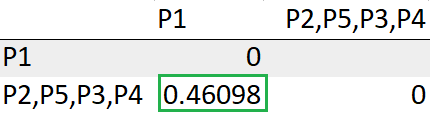
Con esto, terminamos con la obtención de un solo clúster.
Teóricamente, a continuación se muestran los pasos de agrupación:
- Los puntos P3, P4 tienen la menor distancia y están fusionados
- Los puntos P2, P5 tienen la menor distancia y están fusionados
- Los grupos (P3, P4), (P2, P5) están agrupados
- El grupo (P3, P4, P2, P5) se fusiona con el punto de datos P1
Podemos visualizar lo mismo usando un dendrograma.
plt.figure(figsize=(12,5))
plt.title("Dendrogram with Single inkage")
dend = shc.dendrogram(shc.linkage(data[['a', 'b']], method='single'), labels=data.index)
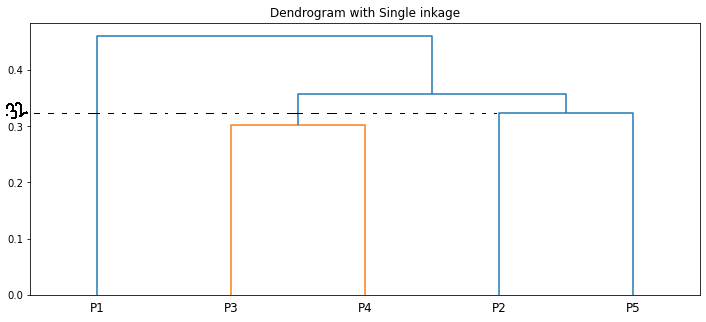
La longitud de las líneas verticales en el dendrograma muestra la distancia. Por ejemplo, la distancia entre los puntos P2, P5 es 0.32388.
La agrupación paso a paso que hicimos es la misma que la del dendrograma🙌
Notas finales:
Al final de este artículo, estamos familiarizados con el trabajo en profundidad de la agrupación jerárquica de enlace único. En el próximo artículo, aprenderemos los otros métodos de vinculación.
Referencias:
Enlace de repositorio de GitHub para pagar Jupyter Notebook
Espero que este blog ayude a comprender el funcionamiento de la agrupación jerárquica de enlace único. Por favor, dale una palmada 👏. Feliz aprendizaje !! 😊
Los medios que se muestran en este artículo no son propiedad de DataPeaker y se utilizan a discreción del autor.






