El árbol comienza con el nodoNodo es una plataforma digital que facilita la conexión entre profesionales y empresas en busca de talento. A través de un sistema intuitivo, permite a los usuarios crear perfiles, compartir experiencias y acceder a oportunidades laborales. Su enfoque en la colaboración y el networking hace de Nodo una herramienta valiosa para quienes desean expandir su red profesional y encontrar proyectos que se alineen con sus habilidades y objetivos.... raíz que consta de los datos completos y, posteriormente, utiliza estrategias inteligentes para dividir los nodos en varias ramas.
El conjunto de datos original se dividió en subconjuntos en este proceso.
Para responder a la pregunta fundamental, su cerebro inconsciente hace algunos cálculos (a la luz de las preguntas de ejemplo que se registran a continuación) y termina comprando la cantidad necesaria de leche. ¿Es normal o entre semana?
Los días laborables requerimos 1 litro de leche.
Es un fin de semana? Los fines de semana necesitamos 1,5 litros de leche.
¿Es correcto decir que estamos anticipando invitados hoy? Necesitamos comprar 250 ML de leche adicional para cada invitado, y así sucesivamente.
Antes de saltar a la idea hipotética de árboles de decisión, ¿qué tal si explicamos inicialmente qué son los árboles de decisión? es más, ¿por qué razón sería una buena idea que los utilicemos?
¿Por qué utilizar árboles de decisión?
Entre otros métodos de aprendizaje supervisadoEl aprendizaje supervisado es un enfoque de machine learning donde un modelo se entrena utilizando un conjunto de datos etiquetados. Cada entrada en el conjunto de datos está asociada a una salida conocida, lo que permite al modelo aprender a predecir resultados para nuevas entradas. Este método es ampliamente utilizado en aplicaciones como la clasificación de imágenes, el reconocimiento de voz y la predicción de tendencias, destacando su importancia en..., sobresalen los algoritmos basados en árboles. Estos son modelos predictivos con mayor precisión y comprensión simple.
¿Cómo funciona el árbol de decisiones?
Hay diferentes algoritmos escritos para ensamblar un árbol de decisiones, que puede ser utilizado por el problema.
A continuación se enumeran algunos de los algoritmos más utilizados:
• CARRITO
• ID3
• C4.5
• CHAID
Ahora explicaremos sobre el algoritmo CHAID paso a paso. Antes de eso, hablaremos un poco sobre chi_square.
chi_square
Chi-Cuadrado es una medidaLa "medida" es un concepto fundamental en diversas disciplinas, que se refiere al proceso de cuantificar características o magnitudes de objetos, fenómenos o situaciones. En matemáticas, se utiliza para determinar longitudes, áreas y volúmenes, mientras que en ciencias sociales puede referirse a la evaluación de variables cualitativas y cuantitativas. La precisión en la medición es crucial para obtener resultados confiables y válidos en cualquier investigación o aplicación práctica.... estadística para encontrar la diferencia entre los nodos secundarios y principales. Para calcular esto, encontramos la diferencia entre los conteos observados y esperados de la variableEn estadística y matemáticas, una "variable" es un símbolo que representa un valor que puede cambiar o variar. Existen diferentes tipos de variables, como las cualitativas, que describen características no numéricas, y las cuantitativas, que representan cantidades numéricas. Las variables son fundamentales en experimentos y estudios, ya que permiten analizar relaciones y patrones entre diferentes elementos, facilitando la comprensión de fenómenos complejos.... objetivo para cada nodo y la suma al cuadrado de estas diferencias estandarizadas nos dará el valor de Chi-cuadrado.
Fórmula
Para encontrar la característica más dominante, las pruebas de chi-cuadrado usarán que también se llama CHAID, mientras que ID3 usa ganancia de información, C4.5 usa la relación de ganancia y CART usa el índiceEl "Índice" es una herramienta fundamental en libros y documentos, que permite ubicar rápidamente la información deseada. Generalmente, se presenta al inicio de una obra y organiza los contenidos de manera jerárquica, incluyendo capítulos y secciones. Su correcta elaboración facilita la navegación y mejora la comprensión del material, convirtiéndolo en un recurso esencial tanto para estudiantes como para profesionales en diversas áreas.... GINI.
Hoy en día, la mayoría de las bibliotecas de programación (por ejemplo, Pandas para Python) utilizan la métrica de Pearson para la correlación de forma predeterminada.
La fórmula de chi-cuadrado: –
√ ((y – y ‘)2 / y ‘)
donde y es real y se espera y ‘.
Conjunto de datos
Vamos a construir reglas de decisión para el siguiente conjunto de datos. La columna de decisión es el objetivo que nos gustaría encontrar en función de algunas características.
Por cierto, ignoraremos la columna del día porque es solo el número de fila.
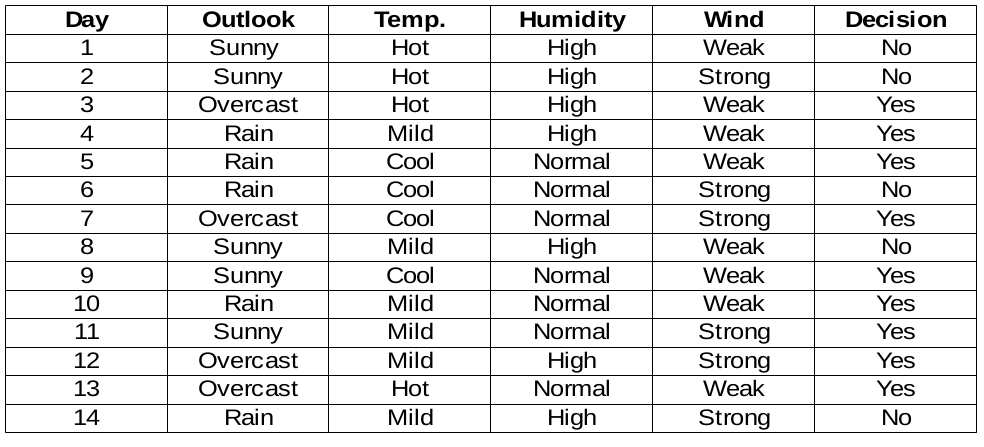
para leer el conjunto de datos de la implementación de Python del archivo CSV a continuación: –
import pandas as pd
data = pd.read_csv("dataset.csv")
data.head()
Necesitamos encontrar la característica más importante en las columnas de destino para elegir el nodo para dividir los datos en este conjunto de datos.
Característica de humedad
Hay dos tipos de la clase presentes en las columnas de humedad: alta y normal. Ahora calcularemos los valores chi_square para ellos.
| sí | No | Total | Esperado | Chi-cuadrado Sí | Chi-cuadrado No | |
| Elevado | 3 | 4 | 7 | 3,5 | 0,267 | 0,267 |
| bajo | 6 | 1 | 7 | 3,5 | 1.336 | 1.336 |
Para cada fila, la columna total es la suma de las decisiones de sí y no. La mitad de la columna total se denomina valores esperados porque hay 2 clases en la decisión. Es fácil calcular los valores de chi-cuadrado basándose en esta tabla.
Por ejemplo,
chi-cuadrado sí para humedad alta es √ ((3– 3,5)2 / 3,5) = 0,267
mientras que el real es 3 y el esperado es 3,5.
Entonces, el valor de chi-cuadrado de la característica de humedad es
= 0,267 + 0,267 + 1,336 + 1,336
= 3.207
Ahora, también encontraremos valores de chi-cuadrado para otras características. La característica que tenga el valor máximo de chi-cuadrado será el punto de decisión. ¿Qué pasa con la función de viento?
Característica de viento
Hay dos tipos de la clase presentes en las columnas de viento: débil y fuerte. La siguiente tabla es la siguiente tabla.
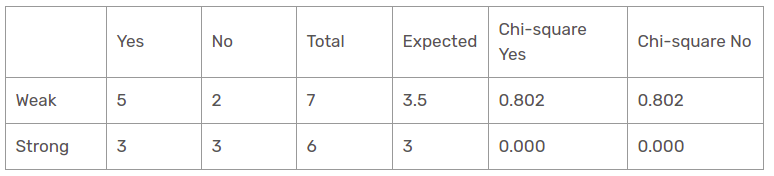
Aquí, el valor de prueba de chi-cuadrado de la característica de viento es
= 0,802 + 0,802 + 0 + 0
= 1,604
Este es también un valor menor que el valor chi-cuadrado de la humedad. ¿Qué pasa con la función de temperatura?
Característica de temperatura
Hay tres tipos de la clase presentes en las columnas de temperatura: caliente, fría y suave. La siguiente tabla es la siguiente tabla.
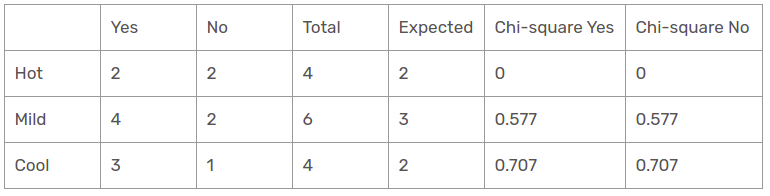
Aquí, el valor de prueba de chi-cuadrado de la característica de temperatura es
= 0 + 0 + 0,577 + 0,577 + 0,707 + 0,707
= 2.569
Este es un valor menor que el valor chi-cuadrado de la humedad y también mayor que el valor chi_square del viento. ¿Qué pasa con la función de Outlook?
Característica de Outlook
Hay tres tipos de clases presentes en las columnas de temperatura: soleado, lluvioso y nublado. La siguiente tabla es la siguiente tabla.
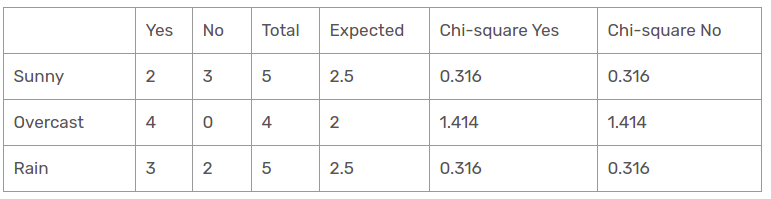
Aquí, el valor de la prueba de chi-cuadrado de la función de perspectiva es
= 0,316 + 0,316 + 1,414 + 1,414 + 0,316 + 0,316
= 4.092
Hemos calculado los valores de chi-cuadrado de todas las características. Veámoslos a todos en una mesa.
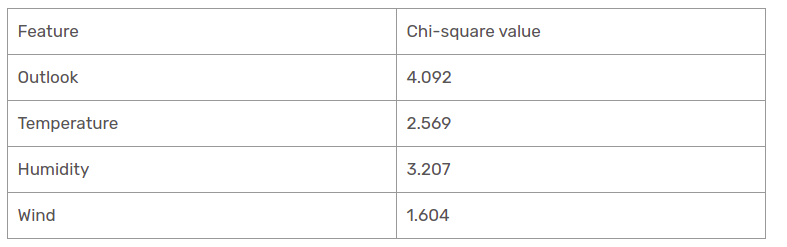
Como se ve, la columna de Outlook tiene el valor de chi-cuadrado más elevado y más alto. Esto implica que es la característica principal del componente. Junto con estos valores, colocaremos esta característica en el nodo raíz.
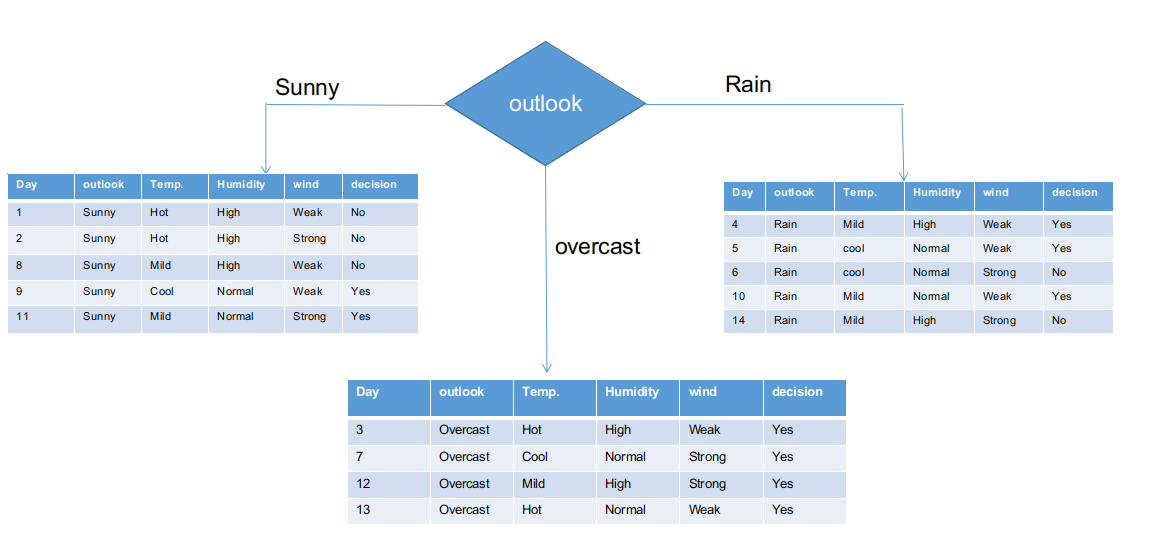
Hemos separado la información sin procesar en función de las clases de Outlook en la ilustración anterior. Por ejemplo, la rama nublada simplemente tiene una decisión afirmativa en el conjunto de datos subinformacional. Esto implica que el árbol CHAID devuelve SÍ si el panorama está nublado.
Tanto las ramas soleadas como las lluviosas tienen decisiones de sí y no. Aplicaremos pruebas de chi-cuadrado para estos conjuntos de datos subinformativos.
Outlook = sucursal soleada
Esta rama tiene 5 ejemplos. Actualmente, buscamos la característica más predominante. Por cierto, ignoraremos la función de Outlook ahora, ya que son completamente iguales. Al final del día, encontraremos las columnas más predominantes entre temperatura, humedad y viento.
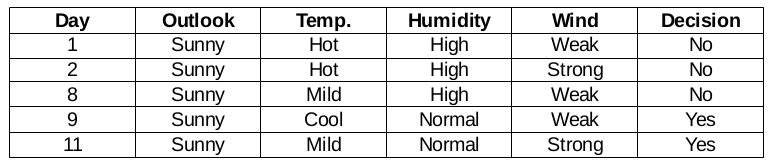
Función de humedad para cuando el panorama es soleado
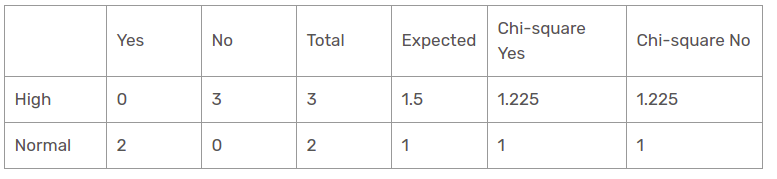
El valor chi-cuadrado de la característica de humedad para una perspectiva soleada es
= 1,225 + 1,225 + 1 + 1
= 4.449
Función de viento para cuando el panorama es soleado
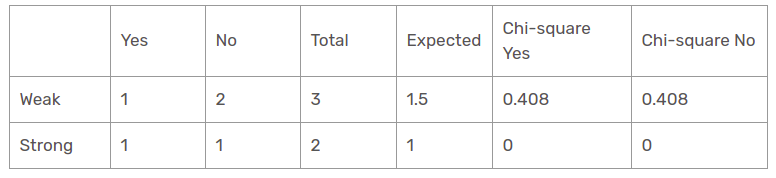
El valor chi-cuadrado de la característica del viento para la perspectiva soleada es
= 0,408 + 0,408 + 0 + 0
= 0,816
Función de temperatura para cuando el panorama es soleado
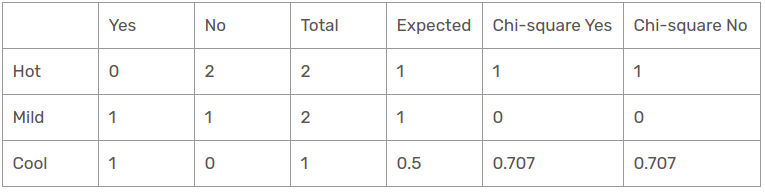
Entonces, el valor chi-cuadrado de la característica de temperatura para la perspectiva soleada es
= 1 + 1 + 0 + 0 + 0,707 + 0,707
= 3.414
Hemos encontrado valores de chi-cuadrado para la perspectiva soleado. Veámoslos a todos en una mesa.
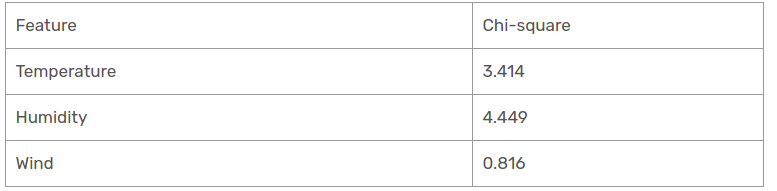
En la actualidad, la humedad es la característica más predominante de la rama de mirador soleado. Pondremos esta característica como regla de decisión.
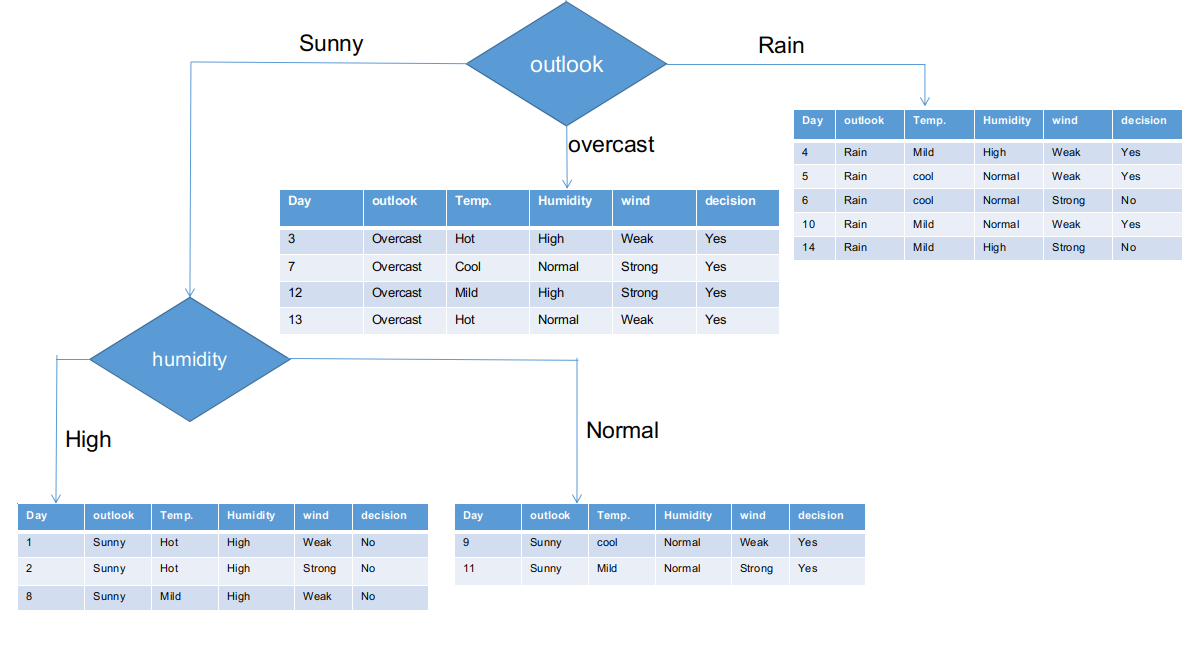
Actualmente, ambas ramas de humedad para la perspectiva soleada tienen solo una decisión como se delineó anteriormente. El árbol CHAID devolverá NO para una perspectiva soleada y alta humedad y devolverá SÍ para una perspectiva soleada y humedad normal.
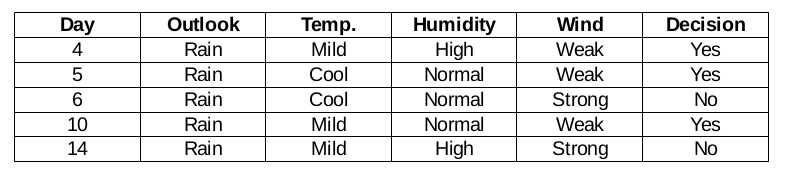
Rama de perspectiva de lluvia
En realidad, esta rama tiene decisiones tanto positivas como negativas. Necesitamos aplicar la prueba de chi-cuadrado para esta rama para encontrar una decisión precisa. Esta rama tiene 5 instancias distintas, como se demuestra en el conjunto de datos de recopilación subinformacional adjunto. ¿Qué tal si averiguamos la característica más predominante entre la temperatura, la humedad y el viento?
Función de viento para pronóstico de lluvia
Hay dos tipos de una clase presente en la característica de viento para la perspectiva de lluvia: débil y fuerte.
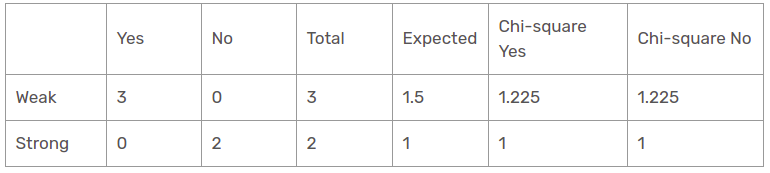
Entonces, el valor chi-cuadrado de la característica de viento para la perspectiva de lluvia es
= 1,225 + 1,225 + 1 + 1
= 4.449
Función de humedad para pronóstico de lluvia
Hay dos tipos de una clase presente en la característica de humedad para la perspectiva de lluvia: alta y normal.
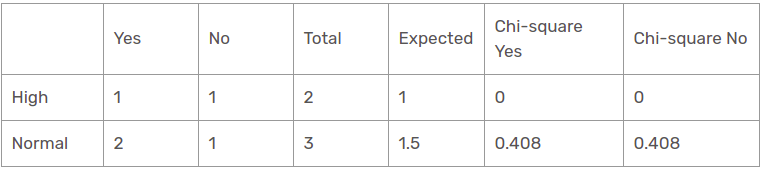
El valor chi-cuadrado de la característica de humedad para la perspectiva de lluvia es
= 0 + 0 + 0.408 + 0.408
= 0,816
Característica de temperatura para pronóstico de lluvia
Hay dos tipos de clases presentes en las características de temperatura para la perspectiva de lluvia, tales como templadas y frescas.

El valor chi-cuadrado de la característica de temperatura para la perspectiva de lluvia es
= 0 + 0 + 0.408 + 0.408
= 0,816
Hemos encontrado que todos los valores de chi-cuadrado para la lluvia es la rama de perspectiva. Veámoslos todos en una sola mesa.
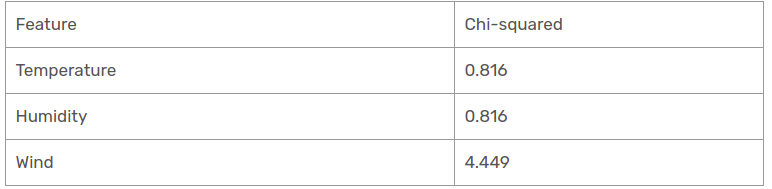
Por lo tanto, la función de viento es la vencedora de la lluvia es la rama de la perspectiva. Coloque esta columna en la rama conectada y vea el conjunto de datos subinformativo correspondiente.
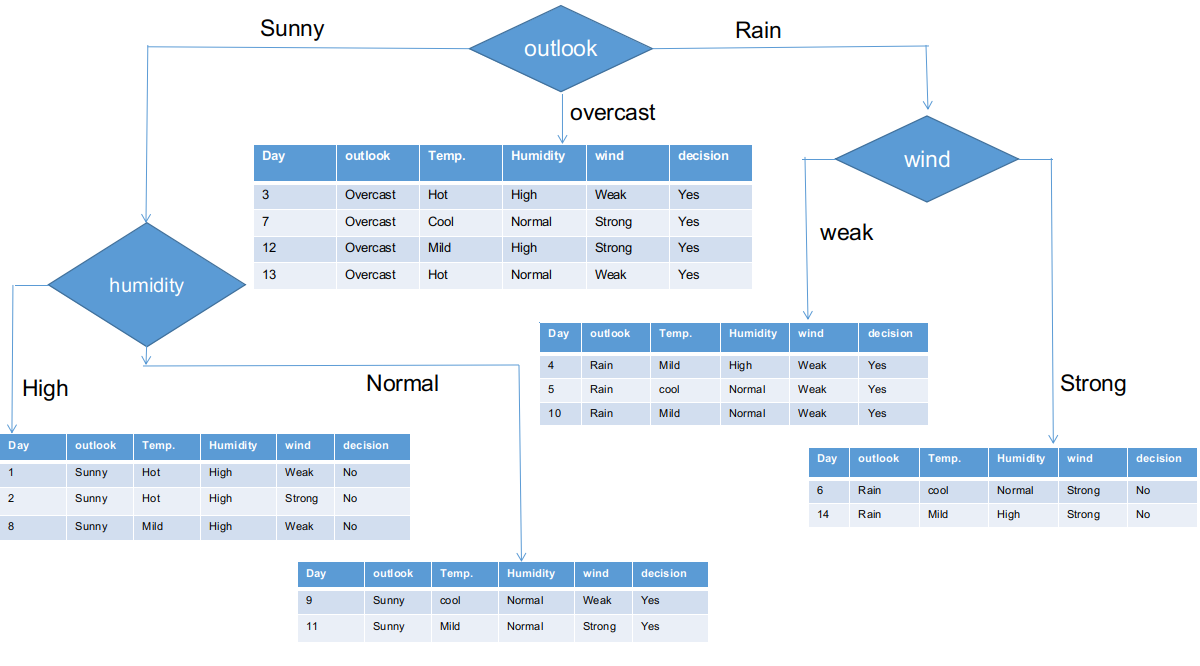
Como se ve, todas las sucursales tienen conjuntos de datos subinformativos con una sola decisión, como sí o no. De esta manera, podemos generar el árbol CHAID como se ilustra a continuación.
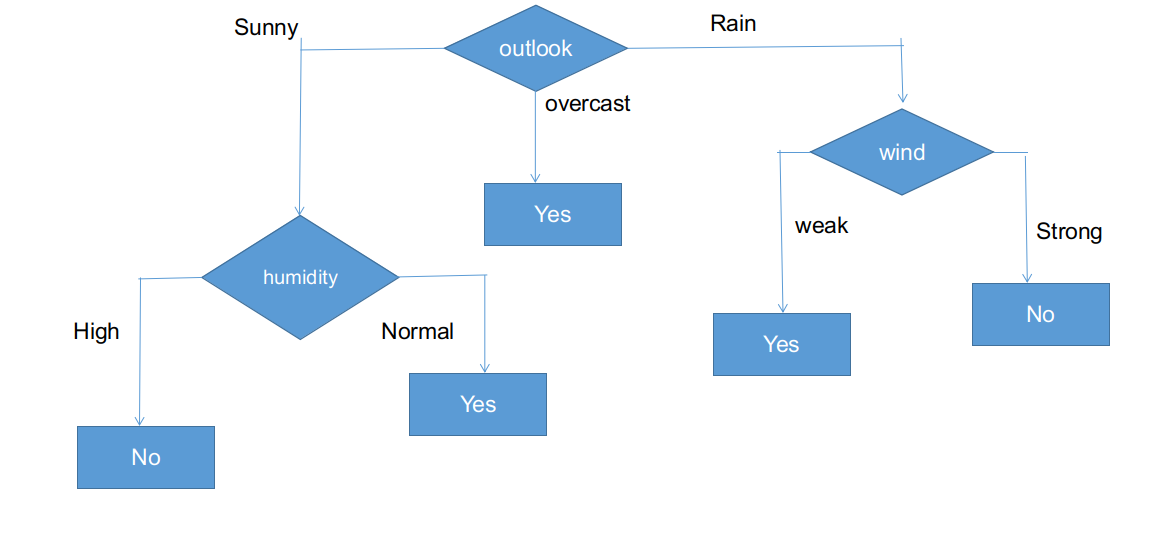
La forma final del árbol CHAID.
Implementación en Python de un árbol de decisiones usando CHAID
from chefboost import Chefboost as cb
import pandas as pd
data = pd.read_csv("/home/kajal/Downloads/weather.csv")
data.head()
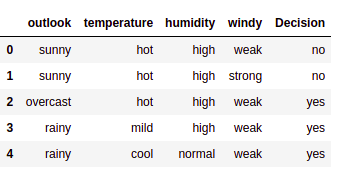
config = {"algorithm": "CHAID"}
tree = cb.fit(data, config)
árbol
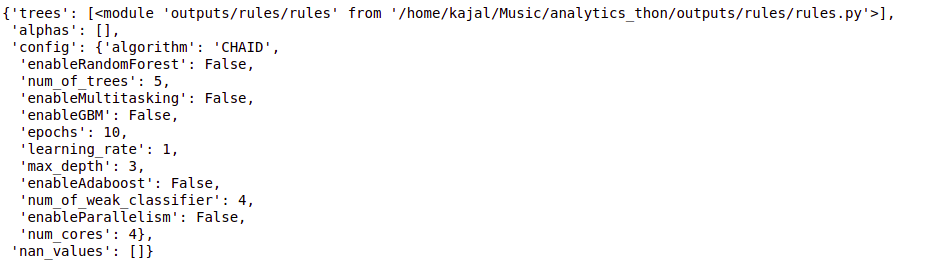
# test_instance = ['sunny','hot','high','weak','no'] test_instance = data.iloc[2] test_instance
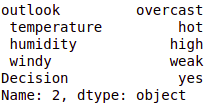
cb.predict(tree,test_instance)
output:- 'Yes'
#obj[0]: outlook, obj[1]: temperature, obj[2]: humidity, obj[3]: windy
# {"feature": "outlook", "instances": 14, "metric_value": 4.0933, "depth": 1}
def findDecision(obj):
if obj[0] == 'rainy':
# {"feature": " windy", "instances": 5, "metric_value": 4.4495, "depth": 2}
if obj[3] == 'weak':
return 'yes'
elif obj[3] == 'strong':
return 'no'
else:
return 'no'
elif obj[0] == 'sunny':
# {"feature": " humidity", "instances": 5, "metric_value": 4.4495, "depth": 2}
if obj[2] == 'high':
return 'no'
elif obj[2] == 'normal':
return 'yes'
else:
return 'yes'
elif obj[0] == 'overcast':
return 'yes'
else:
return 'yes'
Conclusión
Por lo tanto, hemos creado un árbol de decisiones CHAID desde cero para terminar en esta publicación. CHAID utiliza una métrica de medición de chi-cuadrado para descubrir la característica más importante y aplicarla de forma recursiva hasta que los conjuntos de datos subinformativos tengan una única decisión. Aunque se trata de un algoritmo de árbol de decisiones heredado, todavía es el mismo proceso para los problemas de clasificación.
Los medios que se muestran en este artículo no son propiedad de DataPeaker y se utilizan a discreción del autor.






