Este artículo fue publicado como parte del Blogatón de ciencia de datos.
Comprender el problema del sobreajuste en árboles de decisión y resolverlo mediante la poda de complejidad y costo mínimo utilizando Scikit-Learn en Python
Decision Tree es una de las herramientas más intuitivas y efectivas presentes en el conjunto de herramientas de un científico de datos. Tiene una estructura en forma de árbol invertido que alguna vez se usó solo en el análisis de decisiones, pero ahora también es un algoritmo de aprendizaje automático brillante, especialmente cuando tenemos un problema de clasificación en nuestras manos.
Estos árboles de decisión son bien conocidos por su capacidad para capturar patrones en los datos. Pero, el exceso de cualquier cosa es dañino, ¿verdad? Los árboles de decisión son infames ya que pueden aferrarse demasiado a los datos en los que están entrenados.
Por lo tanto, nuestro árbol da malos resultados en la implementación porque no puede lidiar con un nuevo conjunto de valores.
¡Pero no te preocupes! Al igual que un mecánico experto tiene llaves de todos los tamaños disponibles en su caja de herramientas, un científico de datos experto también tiene su conjunto de técnicas para hacer frente a cualquier tipo de problema. Y eso es lo que exploraremos en este artículo.
El papel de la poda en los árboles de decisión
La poda es una de las técnicas que se utiliza para superar nuestro problema de sobreajuste. La poda, en su sentido literal, es una práctica que implica la eliminación selectiva de ciertas partes de un árbol (o planta), como ramas, brotes o raíces, para mejorar la estructura del árbol y promover un crecimiento saludable. Esto es exactamente lo que la poda también hace con nuestros árboles de decisión. Lo hace versátil para que pueda adaptarse si le damos algún tipo de información nueva, solucionando así el problema del sobreajuste.
Reduce el tamaño de un árbol de decisiones, lo que puede aumentar ligeramente el error de entrenamiento, pero disminuir drásticamente el error de prueba, lo que lo hace más adaptable.
Poda de costo mínimo y complejidad es uno de los tipos de poda de árboles de decisión.
Este algoritmo está parametrizado por α (≥0) conocido como parámetro de complejidad.
El parámetro de complejidad se utiliza para definir la medida de costo-complejidad, Rα(T) de un árbol dado T: Rα(T) = R (T) + α | T |
donde | T | es el número de nodos terminales en T y R (T) se define tradicionalmente como la tasa total de clasificación errónea de los nodos terminales.
En su versión 0.22, Scikit-learn introdujo este parámetro llamado ccp_alpha (¡Sí! Es la abreviatura de Poda de complejidad de costos – Alfa) a los árboles de decisión que se pueden utilizar para realizar lo mismo.
Construyendo el árbol de decisiones en Python
Usaremos el conjunto de datos Iris para ajustar el árbol de decisiones. Puede descargar el conjunto de datos aquí.
Primero, importemos las bibliotecas básicas requeridas y el conjunto de datos:
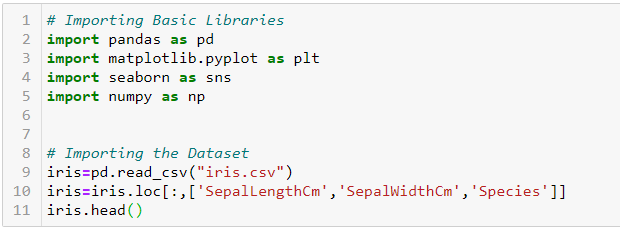
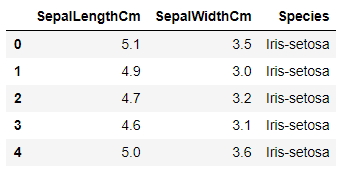
El conjunto de datos se ve así:
Nuestro objetivo es predecir la especie de una flor en función de la longitud y el ancho de su sépalo.
Dividiremos el conjunto de datos en dos partes: entrenar y probar. Estamos haciendo esto para que podamos ver cómo funciona nuestro modelo también en datos invisibles. Usaremos el train_test_split función de sklearn.model_selection para dividir el conjunto de datos.
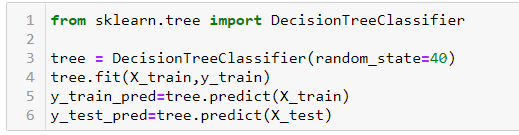
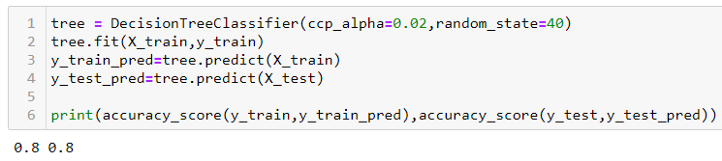
Ahora, ajustemos un árbol de decisiones a la parte del tren y predigamos tanto en la prueba como en el entrenamiento. Usaremos DecisionTreeClassifier de sklearn.tree para este propósito.
De forma predeterminada, la función de árbol de decisión no realiza ninguna poda y permite que el árbol crezca tanto como pueda. Obtenemos una puntuación de precisión de 0,95 y 0,63 en el tren y en la pieza de prueba, respectivamente, como se muestra a continuación. Podemos decir que nuestro modelo está sobreajustado, es decir, memorizando la parte del tren, pero no puede funcionar igualmente bien en la parte de prueba.
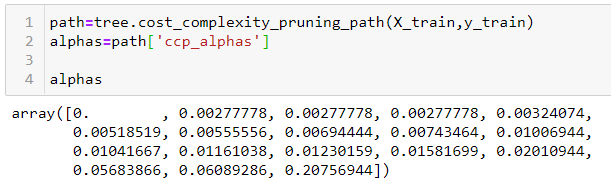
Árbol de decisión en sklearn tiene una función llamada cost_complexity_pruning_path, que da los alfa efectivos de los subárboles durante la poda y también las impurezas correspondientes. En otras palabras, podemos usar estos valores de alfa para podar nuestro árbol de decisiones:
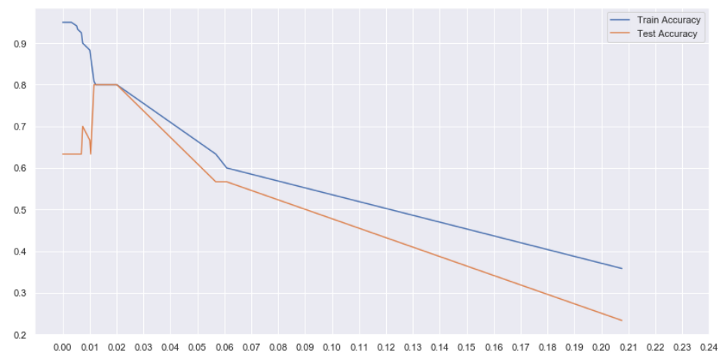
Estableceremos estos valores de alfa y los pasaremos al ccp_alpha parámetro de nuestro DecisionTreeClassifier. Haciendo un bucle sobre el alfas matriz, encontraremos la precisión en las partes de entrenamiento y prueba de nuestro conjunto de datos.
En el gráfico anterior, podemos ver que entre alfa = 0.01 y 0.02, obtenemos la máxima precisión de prueba. Aunque la precisión de nuestro tren ha disminuido a 0,8, nuestro modelo ahora está más generalizado y funcionará mejor con datos invisibles.