Este artículo fue publicado como parte del Blogatón de ciencia de datos.
El algoritmo Random Forest es sin duda uno de los algoritmos más populares entre los científicos de datos. Funciona muy bien tanto en problemas de clasificación como de regresión. Random Forest se conoce como una técnica de conjunto porque es una colección de múltiples árboles de decisión.
¿Cuál fue el objetivo principal de utilizar los árboles de decisiones múltiples?
El uso de un único árbol de decisiones tiene varios inconvenientes. Cuando usamos un único árbol de decisión para resolver el enunciado de un problema, nos encontramos con una situación de bajo sesgo y alta varianza. Es decir, el árbol capturará toda la información sobre los datos de entrenamientoEl entrenamiento es un proceso sistemático diseñado para mejorar habilidades, conocimientos o capacidades físicas. Se aplica en diversas áreas, como el deporte, la educación y el desarrollo profesional. Un programa de entrenamiento efectivo incluye la planificación de objetivos, la práctica regular y la evaluación del progreso. La adaptación a las necesidades individuales y la motivación son factores clave para lograr resultados exitosos y sostenibles en cualquier disciplina...., así como el ruido. Como resultado, el modelo desarrollado usando el algoritmo del árbol de decisión funcionará bien con los datos de entrenamiento, pero tendrá un desempeño deficiente cuando se evalúe en los datos de prueba (datos desconocidos). El sobreajuste es la condición de tener un sesgo bajo y una varianza alta.
Árbol de decisión —————> Sobreajuste ————–> baja desviación alta varianza
Random Forest utiliza múltiples árboles de decisión para evitar este problema presente en el algoritmo del árbol de decisión.
Pero, ¿cómo aborda Random Forest el problema del sobreajuste?
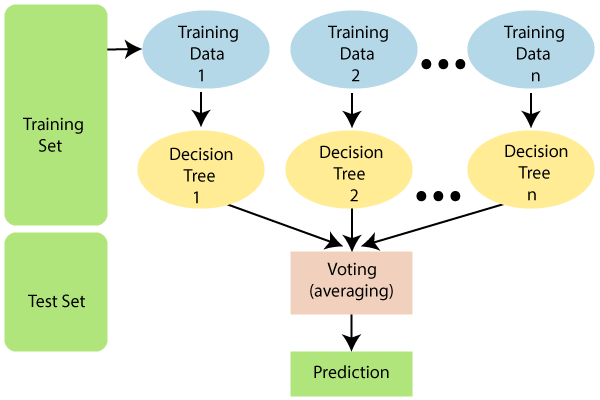
El algoritmo de Random Forest no usa todos los datos de entrenamiento al entrenar el modelo, como se ve en el diagrama a continuación. En su lugar, realiza un muestreo de filas y columnas con repetición. Esto significa que cada árbol solo se puede entrenar con un número limitado de filas y columnas con repetición de datos. En el siguiente diagrama, los datos de entrenamiento 1 se utilizan para entrenar el árbol de decisiones 1, y los datos de entrenamiento n se utilizan para entrenar el árbol de decisiones n. Sin embargo, dado que cada árbol se crea en toda su profundidad y tiene la propiedad de sobreajuste, ¿cómo evitamos este problema?
Dado que el algoritmo no depende del resultado de un árbol de decisión en particular. Primero obtendrá los resultados de todos los árboles de decisión y luego dará el resultado final basado en el tipo de enunciado del problema. Por ejemplo; si el tipo de enunciado del problema es la clasificación, se utilizaría la votación por mayoría. supongamos que estamos clasificando «sí» y «no» con 10 árboles, si 6 árboles están clasificando «sí» y 4 están clasificando «no», la respuesta final será «sí» usando la votación por mayoría. ¿Qué pasa si nuestra salida es una variableEn estadística y matemáticas, una "variable" es un símbolo que representa un valor que puede cambiar o variar. Existen diferentes tipos de variables, como las cualitativas, que describen características no numéricas, y las cuantitativas, que representan cantidades numéricas. Las variables son fundamentales en experimentos y estudios, ya que permiten analizar relaciones y patrones entre diferentes elementos, facilitando la comprensión de fenómenos complejos.... continua? En ese caso, el resultado final sería la media o la medianaLa mediana es una medida estadística que representa el valor central de un conjunto de datos ordenados. Para calcularla, se organizan los datos de menor a mayor y se identifica el número que se encuentra en el medio. Si hay un número par de observaciones, se promedia los dos valores centrales. Este indicador es especialmente útil en distribuciones asimétricas, ya que no se ve afectado por valores extremos.... de la producción de todos los árboles.
Problema de clasificación -> Votación mayoritaria
Problema de regresión -> Media / Mediana
El modelo realiza un muestreo de filas. Sin embargo, el muestreo de características debe realizarse de acuerdo con el tipo de enunciado del problema.
- Si el tipo de declaración del problema es «clasificación».
El número total de características / columnas aleatorias seleccionadas = p ^ ½ o la raíz cuadrada de p,
donde p es el número total de independiente atributos / características presentes en los datos.
- Si el tipo de enunciado del problema es «regresión».
El número total de columnas aleatorias seleccionadas = p / 3.
Random Forest evita el sobreajuste con: –
1) Realización de muestreo de filas y características.
2) Conectando todos los árboles de decisión en paralelo.
¿Por qué se conoce como la técnica Bootstrap Aggregation?
Bosque aleatorio es un tipo de técnica de conjunto, también conocida como agregación bootstrap o harpillera.
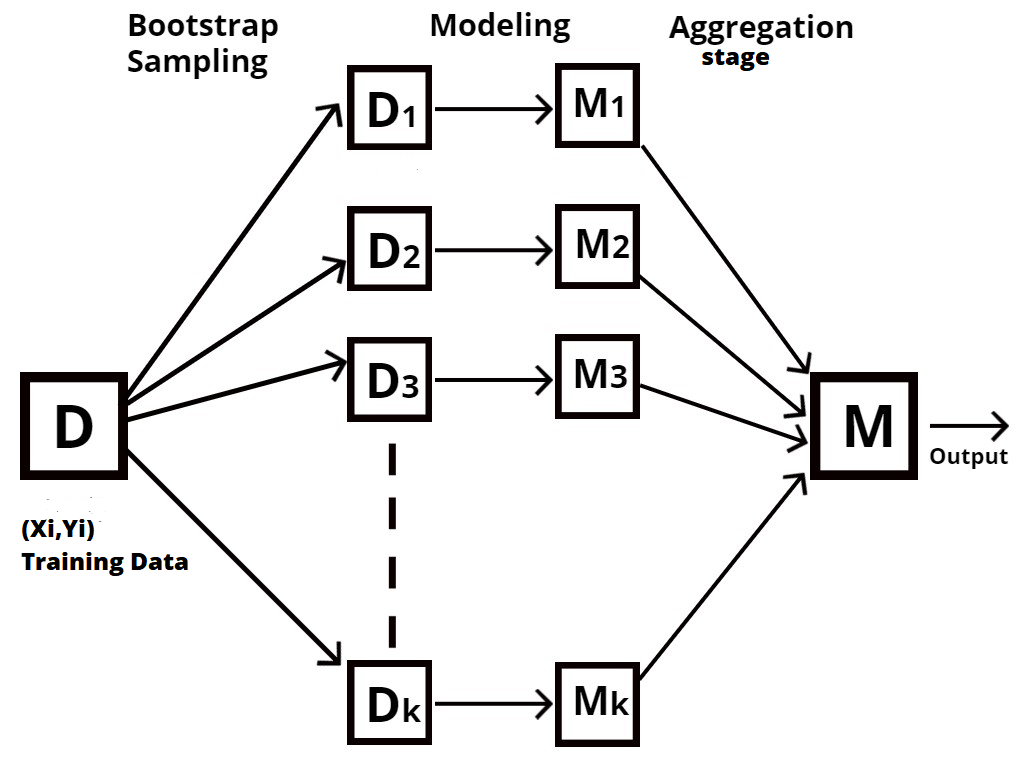
El proceso de muestreo de diferentes filas y características de los datos de entrenamiento con repetición para construir cada modelo de árbol de decisión se conoce como bootstrapping, como se muestra en el siguiente diagrama.
La agregación es el proceso de tomar todos los resultados de cada árbol de decisiones y combinarlos para producir un resultado final utilizando votos mayoritarios o valores promedio, según el tipo de enunciado del problema.
Bosque aleatorio usando R
library(caTools) library(randomForest)
Necesitamos instalar las bibliotecas ‘caTools’ y ‘randomForest’ y activarlas usando la función library ()
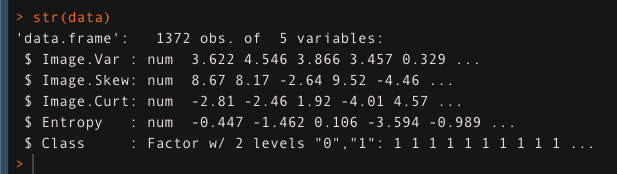
Hemos utilizado el conjunto de datos de autenticación de billetes y lo hemos almacenado en la variable ‘datos’. Comprobaremos la estructura de los datos usando la función str ().
datos <- read.csv ('bank_note_data.csv', header = T)
str (datos)
Ahora dividiremos nuestros datos en partes de prueba y de tren. 80% para entrenamiento y 20% para probar el modelo.
semillas (123)
split <- sample.split (datos, SplitRatio = 0.8)
tren <- subconjunto (datos, dividir == T)
prueba <- subconjunto (datos, división == F)
Después de dividir los datos, construiremos nuestro modelo usando la función randomForest (). Aquí ‘ntree’ es el hiperparámetro. que es necesario ajustar. En este caso, se selecciona como 500.
modelo_aleatorio <- bosque_aleatorio (Clase ~., datos = tren, mtry = 2, ntree = 500)
Predicción de la precisión del modelo en los datos de prueba mediante la función de predicción ().
eval <- predecir (modelo_aleatorio, prueba)
Evaluar la precisión del modelo utilizando la matriz de confusión.
confusionMatrix (tabla (eval, prueba $ Class))
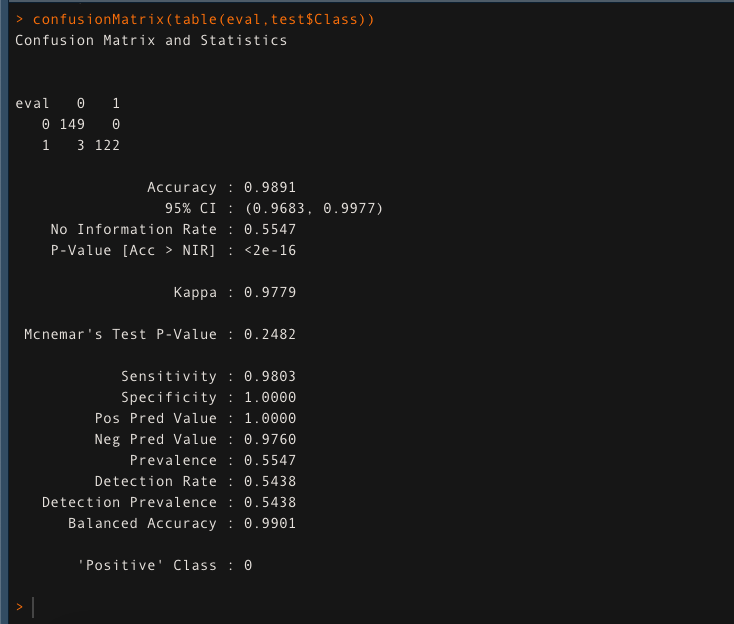
El modelo da una precisión del 98,91% en los datos de prueba. Esto asegura que Random Forest está haciendo un trabajo fantástico.