Este artículo fue publicado como parte del Blogatón de ciencia de datos

Introducción
Aprendiendo. La regresión logística se usa generalmente cuando tenemos que clasificar los datos en dos o más clases. Uno es binario y el otro es regresión logística de clases múltiples. Como sugiere el nombre, la clase binaria tiene 2 clases que son Sí / No, Verdadero / Falso, 0/1, etc. En la clasificación de clases múltiples, hay más de 2 clases para clasificar datos. Pero, antes de irnos, definamos primero la regresión logística:
«La regresión logística es un algoritmo de clasificación para variables categóricas como Sí / No, Verdadero / Falso, 0/1, etc.»
¿En qué se diferencia de la regresión lineal?
Es posible que también haya oído hablar de la regresión lineal. Déjeme decirle que existe una gran diferencia entre la regresión lineal y la regresión logística. La regresión lineal se utiliza para generar valores continuos como el precio de la casa, los ingresos, la población, etc. En la regresión logística, generalmente calculamos la probabilidad que se encuentra entre el intervalo 0 y 1 (ambos inclusive). Entonces la probabilidad se puede usar para clasificar los datos. Por ejemplo, si la probabilidad calculada resulta ser mayor que 0,5, entonces los datos pertenecían a la clase A y, de lo contrario, por menos de 0,5, los datos pertenecían a la clase B.
Pero mi pregunta es si todavía podemos usar la regresión lineal para la clasificación. Mi respuesta será “¡Sí! ¿Por qué no? Pero seguro que es una idea absurda ”. Mi razón será que puede asignar un valor de umbral para la regresión lineal, es decir, si el valor predicho es mayor que el valor de umbral, pertenecía a la clase A; de lo contrario, a la clase B. Pero dará un error grande y un modelo pobre con baja precisión, que realmente no queremos. ¿Derecha? Le sugiero que use solo algoritmos de clasificación.
Ahora veamos el gráfico de regresión lineal que se muestra a continuación.
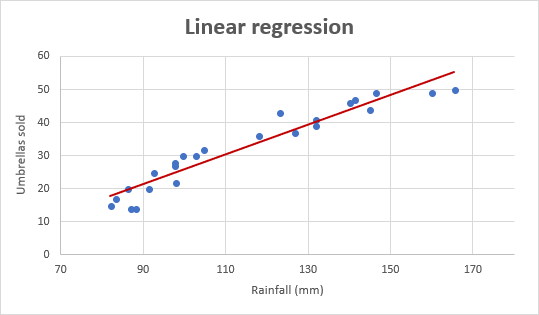
(Cortesía: https://www.ablebits.com/)
El gráfico es una línea recta que pasa por algunos puntos ya que siempre evitamos curvas de sobreajuste y desajuste.
Ahora echemos un vistazo al gráfico de regresión logística:
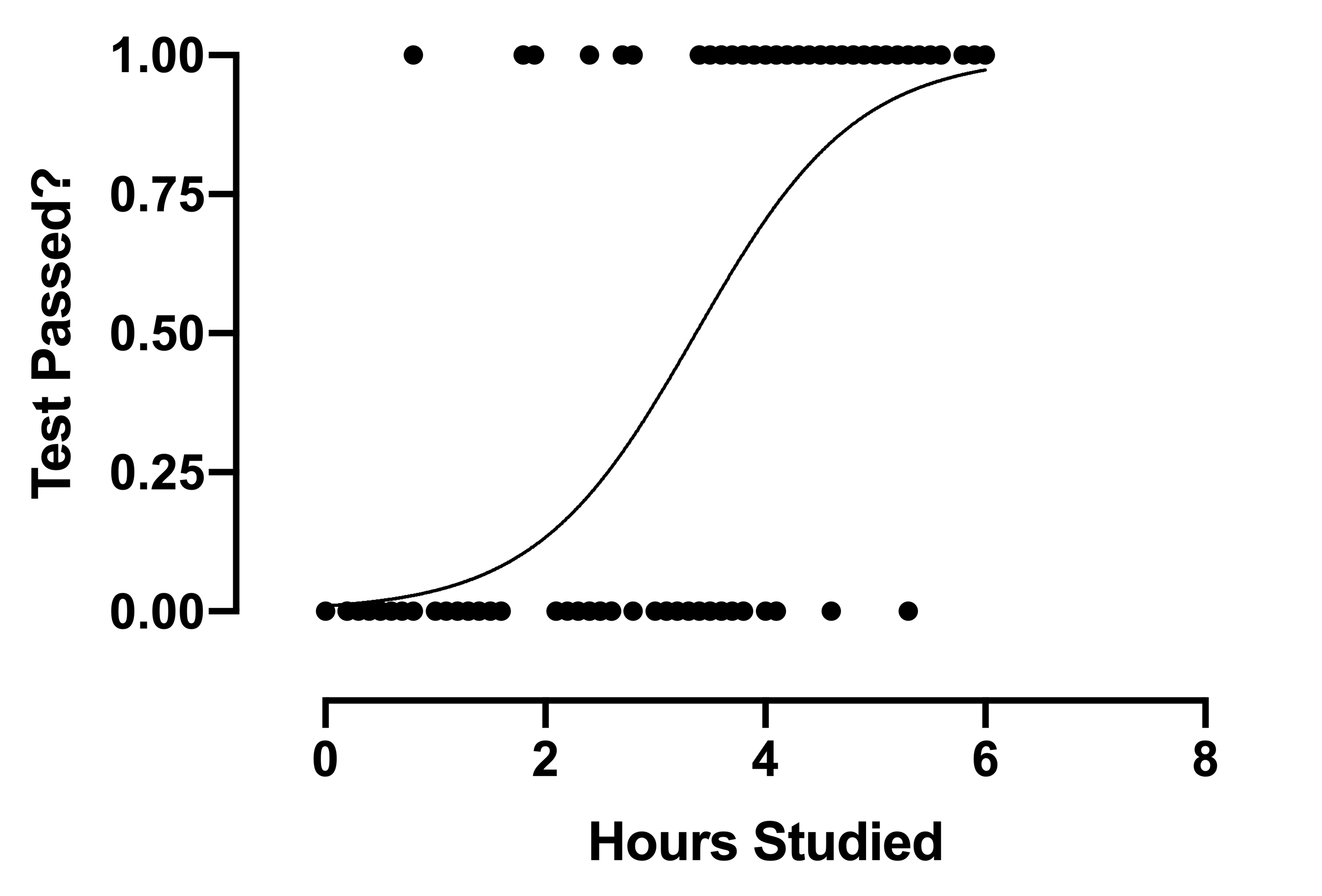
El gráfico es una línea curva en lugar de una línea recta, a diferencia de la regresión lineal.
Ésta es una gran diferencia entre los dos tipos de regresión de los que acabamos de hablar. Entonces mi siguiente pregunta es.
¿Por qué tenemos una línea curva para la regresión logística en lugar de una línea recta?
Para responder a esta pregunta, caminaremos un poco por la regresión lineal y desde allí llegaremos a la curva de regresión logística. ¿Eso está bien? Vamos a empezar.
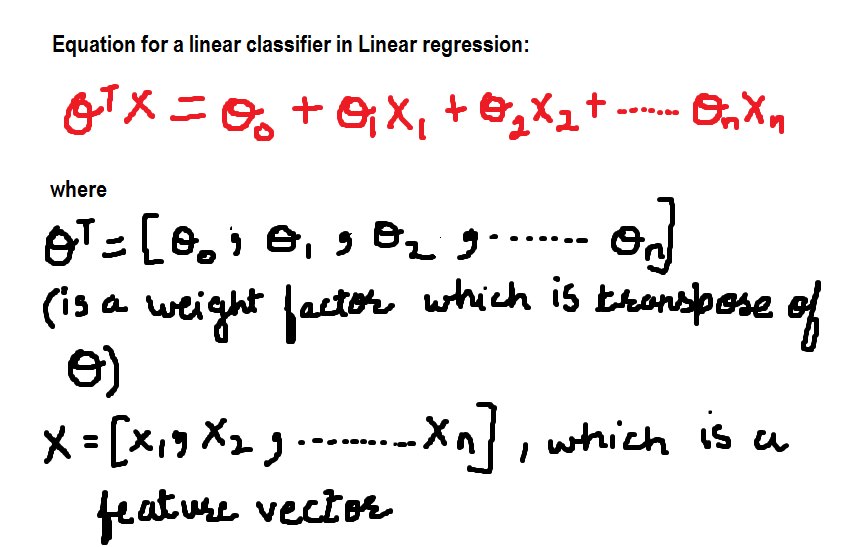
Por ahora, la ecuación para el clasificador lineal es:
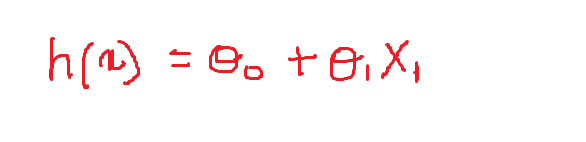
Ahora definiremos los valores de los pesos variables:
theta_0 = -1 y theta = 0.1
Entonces, nuestra ecuación se ve así y la siguiente es la gráfica que representa la ecuación en el plano 2-D:
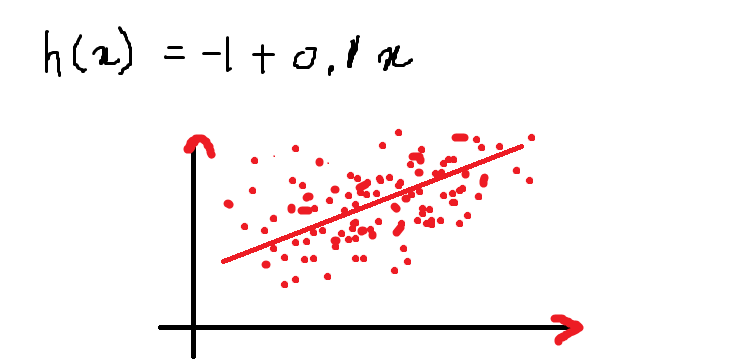
Arriba hay una ecuación de una línea para la ecuación dada:
h (x) = – 1 + 0.1x
El valor de la función h (x) cuando x = 13 es:
h (13) = – 1+ (0,1) * (13) = 0,3
Como se describió anteriormente en este artículo, estoy definiendo el umbral en 0.5, que es cualquier valor de h mayor que (igual a) 0.5 se etiquetará como 1 y, de lo contrario, 0. Podemos definirlo de la siguiente manera en la forma de función de paso:

Ahora, de acuerdo con esto, h tiene un valor de 0.3, de ahí el valor de y_hat = 0 según la función definida anteriormente.
Ahora, una cosa debe tener en cuenta aquí que cada valor mayor que 0.5, suponga que digo que el valor de ‘h’ es 1000 para algún valor de x, entonces se etiquetará como 1 solamente, no hay diferencia entre el valor 1 y 1000 ya que ambos se clasifican como 1 solamente. ¿Es correcto? ¿Podemos aceptar esta solución? ¡Bueno no! ¡¡¡No lo aceptaría !!!
Una cosa más, ¿cuál es la probabilidad de que h tenga un valor de 0.3? Todas estas preguntas quedan sin respuesta. Por estas razones, los científicos de datos no prefieren utilizar la regresión lineal para fines de clasificación.
Antes de continuar, quiero mostrarte cómo se comporta gráficamente la función y_hat:
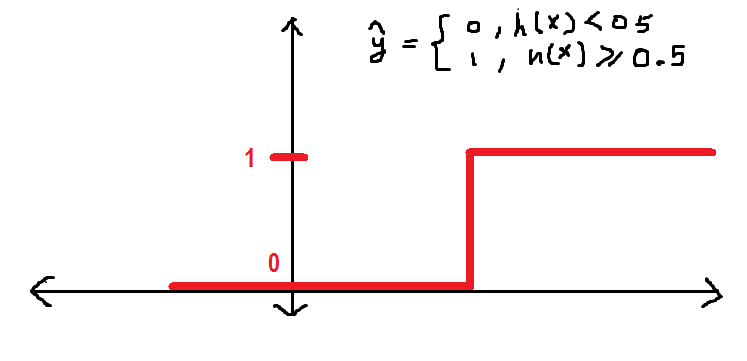
Será mejor si tenemos una curva más suave en lugar de la anterior. Vamos a ver:
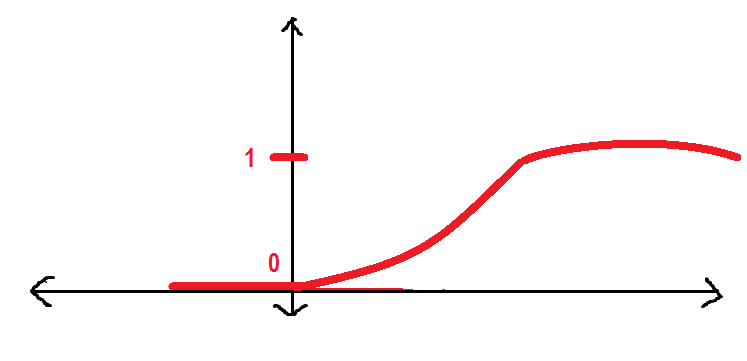
La curva anterior se conoce como Función sigmoidea que usaremos a lo largo de este artículo. Aquí presentaré la función sigmoidea.
¿Qué es la función sigmoidea?
La función sigmoidea está representada por el símbolo sigma. Su comportamiento gráfico se ha descrito en la figura"Figura" es un término que se utiliza en diversos contextos, desde el arte hasta la anatomía. En el ámbito artístico, se refiere a la representación de formas humanas o animales en esculturas y pinturas. En la anatomía, designa la forma y estructura del cuerpo. Además, en matemáticas, "figura" se relaciona con las formas geométricas. Su versatilidad hace que sea un concepto fundamental en múltiples disciplinas.... anterior. La ecuación matemática para la función sigmoidea se describe a continuación:
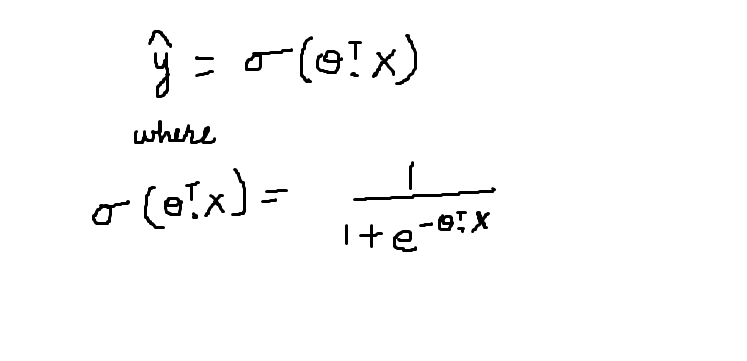
La función sigmoidea da la probabilidad de que los datos pertenezcan a una clase particular que se encuentra en el intervalo [0,1]. Acepta el producto escalar de la transposición de theta y el vector de características X como parámetro. El valor resultante es la probabilidad.
Por lo tanto, cuando P (Y = 1 | X) = sigmoide (theta * X)
P (Y = 0 | X) = 1- sigmoide (theta * X)
Además, quiero que observe el comportamiento de la función sigmoidea:
- Cuando theta (transposición) * X se vuelve mucho más grande, el valor del sigmoide se vuelve igual a 1
- Cuando theta (transposición) * X se vuelve muy pequeño el valor del sigmoide se vuelve igual a 0
Aplicaciones de la regresión logística
En esta sección, me gustaría discutir algunas de las aplicaciones de la regresión logística.
1. Predecir la probabilidad de que una persona sufra un ataque cardíaco
2. Predecir la propensión de un cliente a comprar un producto o suspender una suscripción.
3. Predecir la probabilidad de falla de un proceso o producto dado.
Antes de terminar este artículo, solo quiero recapitular cuándo debe usar la regresión logística:
- Cuando sus datos son binarios: 0/1, Verdadero / Falso, Sí / No
- Cuando necesitas resultados probabilísticos
- Cuando sus datos se pueden separar linealmente
- Cuando necesite comprender el impacto de la función.
Muchos otros algoritmos de clasificación se utilizan ampliamente además de la regresión logística como kNN, árboles de decisión, bosque aleatorio y algoritmos de agrupación como agrupación de k-medias. Pero la regresión logística es un algoritmo ampliamente utilizado y también fácil de implementar.
Así que se trataba del algoritmo de regresión logística para principiantes. Hemos hablado de todo lo que debes saber sobre la teoría de la regresión logística. ¡Espero que hayas disfrutado de mi artículo!
Los medios que se muestran en este artículo no son propiedad de DataPeaker y se utilizan a discreción del autor.






