Análisis de componentes principales | Guía para el análisis de componentes principales

Tabla de contenido

• Introducción

• Descripción general suave

• Contras de usar PCA

• Ejemplo practico

• Conclusión

Introducción

«La inteligencia artificial es el último invento que la humanidad necesitará hacer”. La cita definitivamente deja en claro que el aprendizaje automático es el futuro y grandes oportunidades y beneficios para todos. Que este sea un nuevo comienzo para que aprenda un algoritmo realmente interesante en el aprendizaje automático.

Como todos saben, a menudo nos encontramos con los problemas de almacenar y procesar grandes datos en tareas de aprendizaje automático, ya que es un proceso que requiere mucho tiempo y también surgen dificultades para interpretar. No todas las características de los datos son necesarias para las predicciones. Estos datos ruidosos pueden provocar un mal rendimiento y un sobreajuste del modelo. A través de este artículo, permítame presentarle una técnica de aprendizaje no supervisada PCA (Análisis de componentes principales) que puede ayudarlo a lidiar de manera efectiva con estos problemas hasta cierto punto y brindar resultados de predicción más precisos.

El PCA fue inventado a principios del siglo XX por Karl Pearson, análogo al teorema del eje principal en mecánica y es muy utilizado. A través de este método, realmente transformamos los datos en una nueva coordenada, donde la que tiene la varianza más alta es el componente principal principal. Proporcionándonos así las mejores representaciones de datos posibles.

Resumen suave

Los datos con numerosas características pueden tener correlaciones y duplicaciones en su interior. Entonces, una vez que obtenga los datos, el paso principal es limpiarlos eliminando las características irrelevantes y aplicando técnicas de ingeniería de características que pueden incluso proporcionar mejores resultados que las características originales. Análisis de componentes principales (PCA) es una de esas técnicas mediante la cual son posibles la reducción de dimensionalidad (transformación lineal de atributos existentes) y el análisis multivariado. Tiene varias ventajas, que incluyen la reducción del tamaño de los datos (por lo tanto, una ejecución más rápida), mejores visualizaciones con menos dimensiones, maximiza la varianza, reduce el sobreajuste, etc.

El componente principal en realidad significa las secuencias de vectores de dirección que difieren en función de las líneas de mejor ajuste. También se puede afirmar que estos componentes son vectores propios de la matriz de covarianza. Examinaremos ese concepto a continuación.

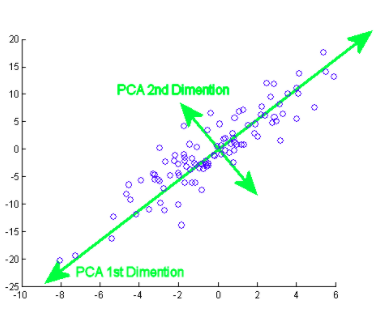
¿Cómo se hace esto? Inicialmente, necesitas encontrar los componentes principales desde diferentes puntos de vista durante la fase de entrenamiento, desde aquellos que recoges los componentes importantes y menos correlacionados e ignoras el resto de ellos, reduciendo así la complejidad. El número de componentes principales puede ser menor o igual al número total de atributos.

Suponga que dos columnas X e Y son las 2 características,

XY

1 4

2 3

3 4

4 6

5 8

Significar

X ‘= 3, Y’ = 5

Covarianza

cov (x, y) = Σ (Xi – X ‘) (Yi – Y’) / n – 1, donde i = 1 an

C = [ cov(x,x) cov (x,y) ]
[cov(y,x) cov(y,y) ]

De manera similar, para más características, encontramos la matriz de covarianza completa con más dimensiones. Al seguir calculando valores propios, vectores, etc., podemos encontrar los componentes principales. La importación de algoritmos y el uso de bibliotecas exactas facilita la identificación de los componentes sin cálculos / operaciones manuales. Tenga en cuenta que el número de autovalores / autovectores le dará el número de dimensiones y la cantidad de varianza asociada con esos componentes.

Ahora bien, como existen numerosos componentes principales para datos grandes, se selecciona principalmente en función de cuál representa la mayor variación posible. Como resultado, los siguientes componentes también se deciden en orden decreciente de varianza de los componentes anteriores ordenando los valores propios, siempre que estos tampoco tengan una correlación con los componentes principales anteriores. Luego descartamos aquellos componentes con menos autovalores / vectores (menos significativos).

En el último paso, usamos vectores de características para orientar los datos a los representados por los componentes principales (Análisis de componentes principales). Esto se hace multiplicando la transposición del conjunto de datos original por la transposición del vector de características.

Contras de usar PCA / Desventajas

Debe tener en cuenta que la estandarización de datos (que también incluye la conversión de variables categóricas en numéricas) es imprescindible antes de usar PCA. Al aplicar PCA, las características independientes se vuelven menos interpretables porque estos componentes principales tampoco son legibles o interpretables. También hay posibilidades de que pierda información durante la PCA.

Ejemplo practico

Ahora, veamos cómo se implementa un algoritmo en un conjunto de datos. Lo guiaré paso a paso a través de cada parte del código.

Echa un vistazo a este conjunto de datos. Este es el famoso conjunto de datos de flores de IRIS, que contiene características como la longitud del sépalo, la longitud del pétalo, el ancho del sépalo y el ancho del pétalo, y la variable objetivo es la especie. Lo que quiere decir con variable objetivo es el valor / clase que necesita predecir, que en este caso es la clase de especie a la que pertenece la flor.

fuente: Wikipedia

Importación de conjuntos de datos y bibliotecas básicas

En primer lugar, comencemos por importar las bibliotecas necesarias,

import numpy as np 
import pandas as pd 
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris

Cargar los datos y mostrar los nombres de las características y clases para su comprensión,

iris = load_iris()
#Feature names and Encoding of target variables
print(iris.feature_names)
print(iris.target_names)
data = pd.DataFrame(iris.data)
data.columns = iris.feature_names
data['CLASS'] = iris.target
data.head()

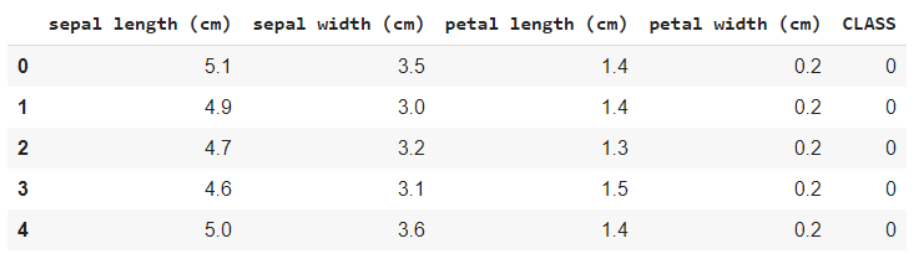
El siguiente fragmento de código le ayuda a obtener un análisis de los datos, a saber cuántas variables son categóricas y cuántas son numéricas. Además, está claro a continuación que todas las filas no son nulas, en caso de que existieran objetos nulos, obtenemos el recuento y las filas / columnas en las que están presentes. Esto nos ayuda a seguir los pasos de preprocesamiento para limpiar los datos.

data.info()

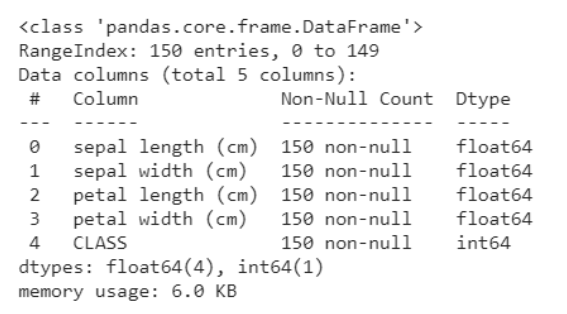
La función data.describe () generalmente proporciona una descripción estadística del conjunto de datos. Estos podrían ser beneficiosos de muchas maneras, puede usar estos datos para completar los valores faltantes o crear una nueva característica, y muchas más.

data.describe()

Aquí está dividiendo los datos en las características y las variables de destino como X e y respectivamente. Y al usar el método de forma, sabe que los datos tienen 150 filas y 5 columnas en total, de las cuales 1 columna es su variable objetivo y otras 4 son las características / atributos.

x = data.iloc[:,:4]  #features
y = data.iloc[:,4] #target
x.shape, y.shape

Fuera: ((150, 4), (150,))

Dado que todas las características son numéricas, es fácil para el modelo para el entrenamiento. Si los datos contenían variables categóricas, primero debemos convertirlas en numéricas, ya que las máquinas / computadoras pueden manejar mejor los números.

Importación de la biblioteca de PCA

from sklearn.decomposition import PCA
pca = PCA()
X = pca.fit_transform(x)
pca.get_covariance()

explained_variance=pca.explained_variance_ratio_
explained_variance

Visualizaciones

with plt.style.context('dark_background'):
    plt.figure(figsize=(6, 4))
    plt.bar(range(4), explained_variance, alpha=0.5, align='center',
            label="individual explained variance")roduction
    plt.ylabel('Explained variance ratio')
    plt.xlabel('Principal components')
    plt.legend(loc="best")
    plt.tight_layout()

De las visualizaciones se obtiene la intuición de que hay principalmente solo 3 componentes con una varianza significativa, por lo tanto, seleccionamos el número de componentes principales como 3.

pca = PCA(n_components=3)
X = pca.fit_transform(x)

Prueba de tren dividida

La división de pruebas de trenes es un método común de capacitación y evaluación. Por lo general, las predicciones sobre los datos entrenados en sí pueden llevar a un sobreajuste, dando así malos resultados para datos desconocidos. En este caso, al dividir los datos en conjuntos de entrenamiento y prueba, usted entrena y luego predice usando el modelo en 2 conjuntos diferentes, resolviendo así el problema del sobreajuste.

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3, random_state=20, stratify=y)

Entrenamiento de modelos

Nuestro objetivo es identificar la clase / especie a la que pertenece la flor dadas algunas de sus características. Por lo tanto, este es un problema de clasificación y el modelo que usamos utiliza K vecinos más cercanos.

from sklearn.neighbors import KNeighborsClassifier
model = KNeighborsClassifier(7)
model.fit(X_train,y_train)
y_pred = model.predict(X_test)

Predicciones

from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score
cm = confusion_matrix(y_test, y_pred)  #confusion matrix
print(cm)
print(accuracy_score(y_test, y_pred))

La matriz de confusión le mostrará el recuento de falsos positivos, falsos negativos, verdaderos positivos y verdaderos negativos.

La puntuación de precisión le indicará en qué medida nuestro modelo ha sido eficaz a la hora de ofrecer predicciones para nuevos datos. El 97% es una muy buena puntuación, y por eso podemos decir que el nuestro es un buen modelo.

Puede ver el código completo en esta colaboración de google previsto.

Conclusión

Realmente espero que haya tenido intuición sobre PCA y también esté familiarizado con el ejemplo discutido anteriormente. No es tan complejo de digerir, solo mantén la concentración. Asegúrese de leer esto una vez más si lo encuentra útil y desarrolle el algoritmo usted mismo para comprenderlo mejor.

Que tenga un lindo día !! 🙂

Relacionado