Introducción
Los datos están en todas partes a nuestro alrededor, en hojas de cálculo, en varias plataformas de redes sociales, en formularios de encuestas y más. El proceso de limpieza, transformación, interpretación, análisis y visualización de estos datos para extraer información útil y obtener información valiosa para tomar decisiones comerciales más efectivas se denomina Análisis de datos.
El análisis de datos se puede organizar en 6 tipos
- Análisis exploratorio
- Análisis descriptivo
- Análisis inferencial
- Análisis predictivo
- Análisis causal
- Análisis mecanicista
Aquí, nos sumergiremos profundamente en Análisis exploratorio,
Análisis exploratorio
El análisis preliminar de datos para descubrir relaciones entre medidas en los datos y para obtener una idea de las tendencias, patrones y relaciones entre varias entidades presentes en el conjunto de datos con la ayuda de estadísticas y herramientas de visualización se denomina Análisis de datos exploratorios (EDA). .
El análisis de datos exploratorios se clasifica de forma cruzada de dos formas diferentes en las que cada método es gráfico o no gráfico. Y luego, cada método es univariado, bivariado o multivariado.
Análisis univariado
Uni significa una y variable significa variable, por lo que en el análisis univariante, solo hay una variable confiable. El objetivo del análisis univariado es derivar los datos, definirlos y resumirlos y analizar el patrón presente en ellos. En un conjunto de datos, explora cada variable por separado. Es posible para dos tipos de variables: categóricas y numéricas.
Algunos patrones que se pueden identificar fácilmente con el análisis univariado son Tendencia central (media, moda y mediana), Dispersión (rango, varianza), Cuartiles (rango intercuartílico) y Desviación estándar.
Los datos univariados se pueden describir mediante:
Ø Tablas de distribución de frecuencia
La tabla de distribución de frecuencias refleja la frecuencia con la que ha ocurrido una ocurrencia en los datos. Da una breve idea de los datos y facilita la búsqueda de patrones.
Ejemplo:
La lista de puntajes de CI es: 118, 139, 124, 125, 127, 128, 129, 130, 130, 133, 136, 138, 141, 142, 149, 130, 154.
| Rango de IQ | Número |
| 118-125 | 3 |
| 126-133 | 7 |
| 134-141 | 4 |
| 142-149 | 2 |
| 150-157 | 1 |
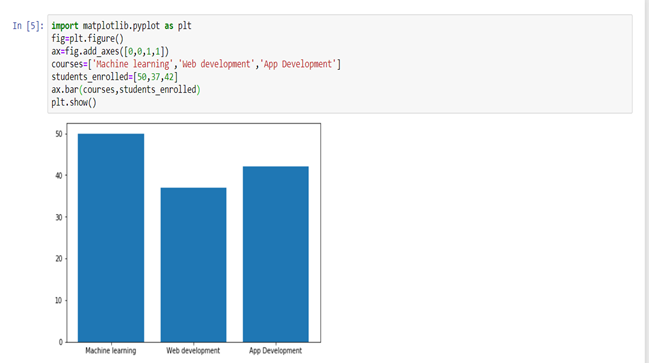
Ø Gráfica de barras
El gráfico de barras es muy conveniente al comparar categorías de datos o diferentes grupos de datos. Ayuda a realizar un seguimiento de los cambios a lo largo del tiempo. Es mejor para visualizar datos discretos.
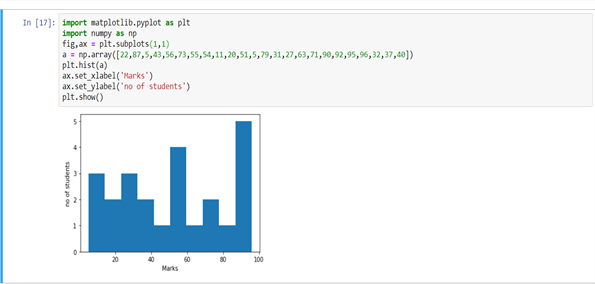
Ø HistogramasLos histogramas son representaciones gráficas que muestran la distribución de un conjunto de datos. Se construyen dividiendo el rango de valores en intervalos, o "bins", y contando cuántos datos caen en cada intervalo. Esta visualización permite identificar patrones, tendencias y la variabilidad de los datos de manera efectiva, facilitando el análisis estadístico y la toma de decisiones informadas en diversas disciplinas....
Los histogramas son similares a los gráficos de barras y muestran las mismas variables categóricas en la categoría de datos. Los histogramas muestran estas categorías como contenedores que indican el número de puntos de datos en un rango. Es mejor para visualizar datos continuos.
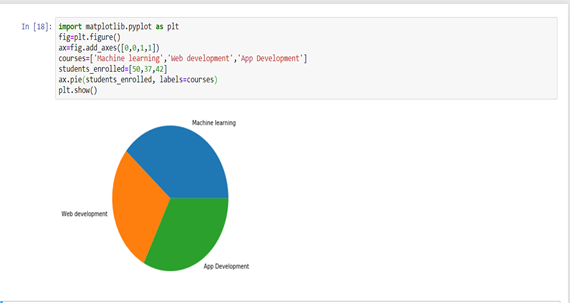
Ø Gráficos circulares
Los gráficos circulares se utilizan principalmente para comprender cómo se divide un grupo en partes más pequeñas. Todo el pastel representa el 100 por ciento y las porciones denotan el tamaño relativo de esa categoría en particular.
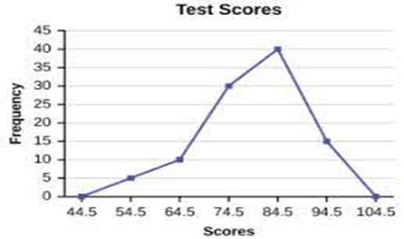
Ø Polígonos de frecuencia
De manera similar a los histogramas, un polígono de frecuencia se usa para comparar conjuntos de datos o mostrar la distribución de frecuencia acumulada.
Análisis bivariado
Bi significa dos y variable significa variable, por lo que aquí hay dos variables. El análisis está relacionado con la causa y la relación entre las dos variables. Hay tres tipos de análisis bivariados.
Análisis bivariado de dos variables numéricas (Numérico-Numérico)
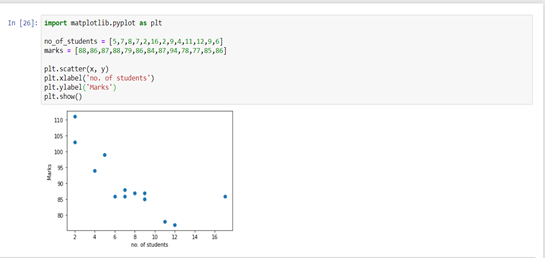
Ø Gráfico de dispersiónUn gráfico de dispersión es una representación visual que muestra la relación entre dos variables numéricas mediante puntos en un plano cartesiano. Cada eje representa una variable, y la ubicación de cada punto indica su valor en relación con ambas. Este tipo de gráfico es útil para identificar patrones, correlaciones y tendencias en los datos, facilitando el análisis y la interpretación de relaciones cuantitativas....
A El gráfico de dispersión representa datos individuales mediante puntos. Estos gráficos facilitan ver si dos variables están relacionadas entre sí. El patrón resultante indica el tipo (lineal o no lineal) y la fuerza de la relación entre dos variables.
Ø Correlación lineal
Lineal Correlation representa la fuerza de una relación lineal entre dos variables numéricas. Si no hay correlación entre las dos variables, no hay tendencia a cambiar junto con los valores de la segunda cantidad.
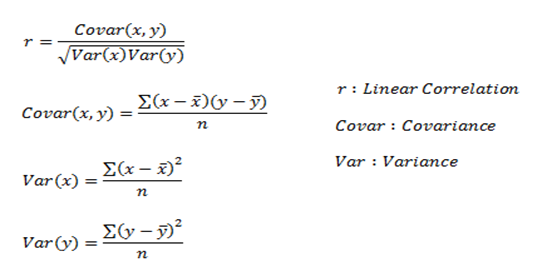
Aquí, r mide la fuerza de una relación lineal y siempre está entre -1 y 1 donde -1 denota una correlación lineal negativa perfecta y +1 denota una correlación lineal positiva perfecta y cero indica que no hay correlación lineal.
Análisis bivariado de dos variables categóricas (Categórico-Categórico)
Ø Prueba de chi-cuadrado
La prueba de chi-cuadrado se utiliza para determinar la asociación entre variables categóricas. Se calcula en función de la diferencia entre las frecuencias esperadas y las frecuencias observadas en una o más categorías de la tabla de frecuencias. Una probabilidad de cero indica una dependencia completa entre dos variables categóricas y una probabilidad de uno indica que dos variables categóricas son completamente independientes.
Aquí, el subíndice c indica los grados de libertad, O indica el valor observado y E indica el valor esperado.
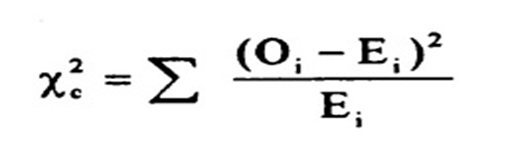
Análisis bivariado de una variableEn estadística y matemáticas, una "variable" es un símbolo que representa un valor que puede cambiar o variar. Existen diferentes tipos de variables, como las cualitativas, que describen características no numéricas, y las cuantitativas, que representan cantidades numéricas. Las variables son fundamentales en experimentos y estudios, ya que permiten analizar relaciones y patrones entre diferentes elementos, facilitando la comprensión de fenómenos complejos.... numérica y una categórica (Numérico-Categórico)
Ø Prueba Z y prueba t
Las pruebas Z y T son importantes para calcular si la diferencia entre una muestra y una población es sustancial.
Si la probabilidad de Z es pequeña, la diferencia entre los dos promedios es más significativa.
Prueba T
Si el tamaño de la muestra es lo suficientemente grande, usamos una prueba Z, y para un tamaño de muestra pequeño, usamos una prueba T.
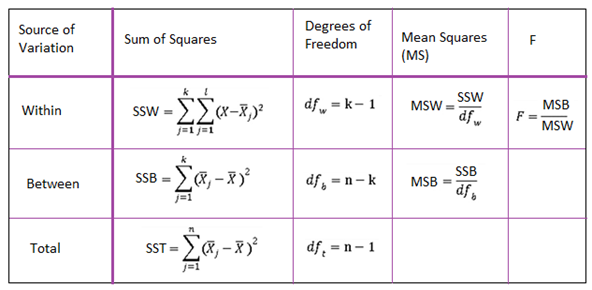
Ø ANÁLISIS DE VARIANZA (ANOVA)
La prueba ANOVA se utiliza para determinar si existe una diferencia significativa entre los promedios de más de dos grupos que son estadísticamente diferentes entre sí. Este análisis es apropiado para comparar los promedios de una variable numérica para más de dos categorías de una variable categórica.
Analisis multivariable
El análisis multivariado es necesario cuando se deben analizar más de dos variables simultáneamente. Es una tarea tremendamente difícil para el cerebro humano visualizar una relación entre 4 variables en un gráfico y, por lo tanto, el análisis multivariado se utiliza para estudiar conjuntos de datos más complejos. Los tipos de análisis multivariante incluyen análisis de conglomerados, análisis factorial, análisis de regresión múltiple, análisis de componentes principales, etc. Existen más de 20 formas diferentes de realizar análisis multivariante y cuál elegir depende del tipo de datos y el objetivo final a lograr. Las formas más comunes son:
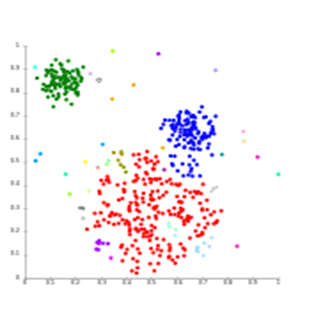
Ø Análisis de conglomerados
El análisis de conglomerados clasifica diferentes objetos en conglomerados de manera que la similitud entre dos objetos del mismo grupo sea máxima y mínima en caso contrario. Se utiliza cuando las filas y columnas del La tabla de datos representa las mismas unidades y la medida representa la distancia o similitud.
Ø Análisis de componentes principales (PCA)
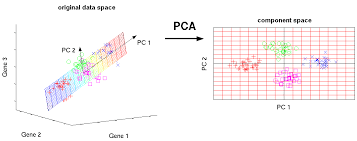
El análisis de componentes principales (o PCA) se utiliza para reducir la dimensionalidad de una tabla de datos con una gran cantidad de medidas interrelacionadas. Aquí, las variables originales se convierten en un nuevo conjunto de variables, que se conocen como los «Componentes principales» del análisis de componentes principales.
PCA se utiliza para el conjunto de datos que muestra multicolinealidad. Aunque las estimaciones de mínimos cuadrados están sesgadas, la distancia entre las varianzas y su valor real puede ser realmente grande. Entonces, PCA agrega algo de sesgo y reduce el error estándar para el modelo de regresión.
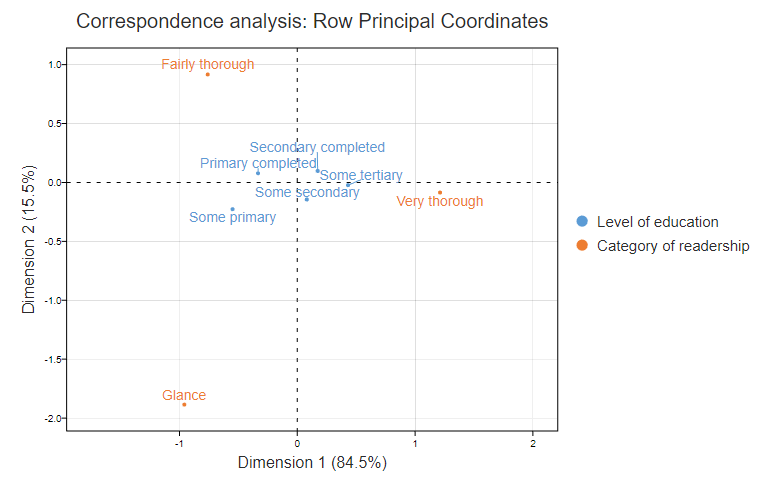
Ø Análisis de correspondencia
El análisis de correspondencia utilizando los datos de una tabla de contingencia muestra las relaciones relativas entre dos grupos diferentes de variables. Una tabla de contingencia es una tabla 2D con filas y columnas como grupos de variables.
Conclusión
Espero que ahora comprenda mejor las diversas técnicas que se utilizan en el análisis univariante, bivariado y multivariado.
Los medios que se muestran en este artículo no son propiedad de DataPeaker y se utilizan a discreción del autor.
