Apoyar el algoritmo de máquina vectorial en el aprendizaje automático

Nota: este artículo se publicó originalmente en octubre 6 de, 2015 y actualizado el 13 de septiembre de 2017

Visión general

• Explicación de la máquina de vectores de soporte (SVM), un algoritmo o clasificación de aprendizaje automático popular
• Implementación de SVM en R y Python
• Conozca los pros y los contras de Support Vector Machines (SVM) y sus diferentes aplicaciones

Introducción

Masterización algoritmos de aprendizaje automático no es un mito en absoluto. La mayoría de los principiantes comienzan aprendiendo la regresión. Es simple de aprender y usar, pero ¿resuelve eso nuestro propósito? ¡Por supuesto no! ¡Porque puedes hacer mucho más que una simple regresión!

Piense en los algoritmos de aprendizaje automático como un arsenal repleto de hachas, espadas, hojas, arcos, dagas, etc. Tiene varias herramientas, pero debe aprender a usarlas en el momento adecuado. Como analogía, piense en ‘Regresión’ como una espada capaz de cortar y cortar datos de manera eficiente, pero incapaz de manejar datos muy complejos. Por el contrario, ‘Support Vector Machines’ es como un cuchillo afilado: funciona en conjuntos de datos más pequeños, pero en conjuntos complejos, puede ser mucho más fuerte y poderoso en la construcción de modelos de aprendizaje automático.

A estas alturas, espero que haya dominado Random Forest, el algoritmo Naive Bayes y Modelado de conjuntos. Si no, le sugiero que saque unos minutos y lea sobre ellos también. En este artículo, lo guiaré a través de los conceptos básicos para el conocimiento avanzado de un algoritmo crucial de aprendizaje automático, máquinas de vectores de apoyo.

Puede obtener información sobre Support Vector Machines en formato de curso aquí (¡es gratis!):

Si es un principiante que busca comenzar su viaje de ciencia de datos, ¡ha venido al lugar correcto! Consulte los cursos completos a continuación, seleccionados por expertos de la industria, que hemos creado solo para usted:

Comprender el algoritmo de Support Vector Machine a partir de ejemplos (junto con el código)

Tabla de contenido

1. ¿Qué es Support Vector Machine?
2. ¿Como funciona?
3. ¿Cómo implementar SVM en Python y R?
4. ¿Cómo ajustar los parámetrosLos "parámetros" son variables o criterios que se utilizan para definir, medir o evaluar un fenómeno o sistema. En diversos campos como la estadística, la informática y la investigación científica, los parámetros son fundamentales para establecer normas y estándares que guían el análisis y la interpretación de datos. Su adecuada selección y manejo son cruciales para obtener resultados precisos y relevantes en cualquier estudio o proyecto.... de SVM?
5. Pros y contras asociados con SVM

¿Qué es la máquina de vectores de soporte?

«Support Vector Machine» (SVM) es un sistema supervisado algoritmo de aprendizaje automático que se puede utilizar para desafíos de clasificación o regresión. Sin embargo, se utiliza principalmente en problemas de clasificación. En el algoritmo SVM, trazamos cada elemento de datos como un punto en el espacio n-dimensional (donde n es un número de características que tiene) con el valor de cada característica siendo el valor de una coordenada particular. Luego, realizamos la clasificación encontrando el hiperplano que diferencia muy bien las dos clases (mira la instantánea a continuación).

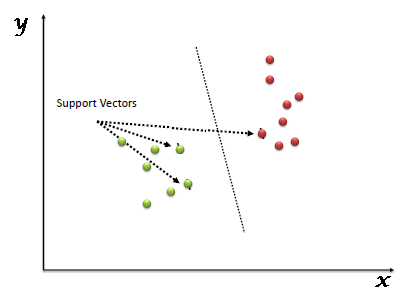
Los vectores de soporte son simplemente las coordenadas de la observación individual. El clasificador SVM es una frontera que mejor segrega las dos clases (hiperplano / línea).

Puede ver máquinas de vectores de soporte y algunos ejemplos de su funcionamiento aquí.

¿Como funciona?

Arriba, nos acostumbramos al proceso de segregación de las dos clases con un hiperplano. Ahora la pregunta candente es «¿Cómo podemos identificar el hiperplano correcto?». ¡No te preocupes, no es tan difícil como crees!

Entendamos:

• Identifique el hiperplano correcto (Escenario-1): Aquí, tenemos tres hiperplanos (A, B y C). Ahora, identifique el hiperplano correcto para clasificar estrellas y círculos.
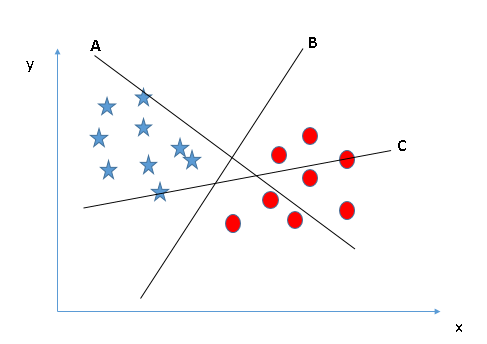  Debe recordar una regla del pulgar para identificar el hiperplano correcto: «Seleccione el hiperplano que segrega mejor las dos clases». En este escenario, el hiperplano «B» ha realizado este trabajo de manera excelente.
• Identifique el hiperplano correcto (Escenario-2): Aquí, tenemos tres hiperplanos (A, B y C) y todos están segregando bien las clases. Ahora, ¿cómo podemos identificar el hiperplano correcto?

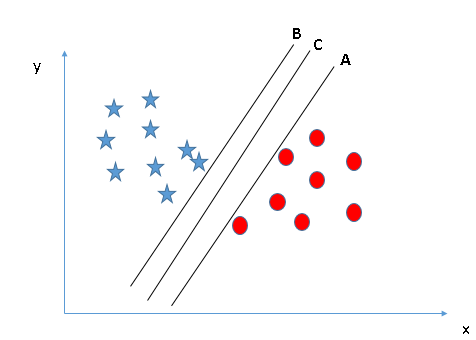  Aquí, maximizar las distancias entre el punto de datos más cercano (cualquier clase) y el hiperplano nos ayudará a decidir el hiperplano correcto. Esta distancia se llama MargenEl margen es un término utilizado en diversos contextos, como la contabilidad, la economía y la impresión. En contabilidad, se refiere a la diferencia entre los ingresos y los costos, lo que permite evaluar la rentabilidad de un negocio. En el ámbito editorial, el margen es el espacio en blanco alrededor del texto en una página, que facilita la lectura y proporciona una presentación estética. Su correcta gestión es esencial.... Veamos la siguiente instantánea: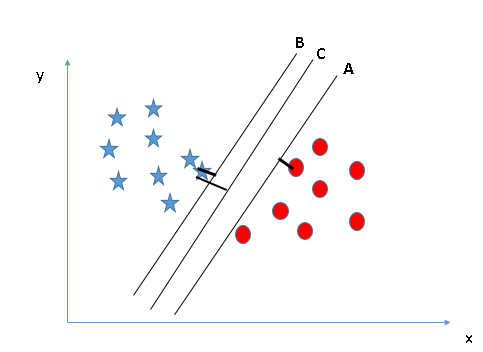
  Arriba, puede ver que el margen para el hiperplano C es alto en comparación con A y B. Por lo tanto, nombramos el hiperplano derecho como C.Otra razón relámpago para seleccionar el hiperplano con un margen más alto es la robustez. Si seleccionamos un hiperplano que tiene un margen bajo, existe una gran posibilidad de clasificación errónea.

• Identifique el hiperplano correcto (Escenario-3):Insinuación: Use las reglas como se discutió en la sección anterior para identificar el hiperplano correcto

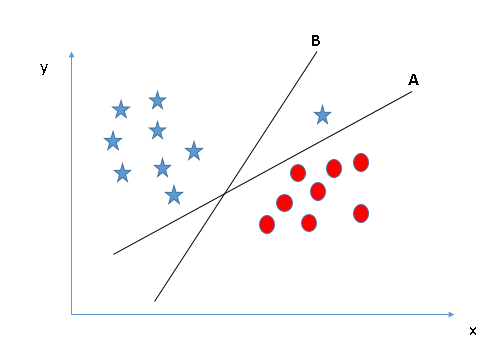Algunos de ustedes pueden haber seleccionado el hiperplano B ya que tiene un margen más alto en comparación con UNA. Pero, aquí está la trampa, SVM selecciona el hiperplano que clasifica las clases con precisión antes de maximizar el margen. Aquí, el hiperplano B tiene un error de clasificación y A lo ha clasificado todo correctamente. Por lo tanto, el hiperplano derecho es UNA.

• ¿Podemos clasificar dos clases (Escenario-4) ?: A continuación, no puedo segregar las dos clases usando una línea recta, ya que una de las estrellas se encuentra en el territorio de la otra clase (círculo) como un valor atípico.
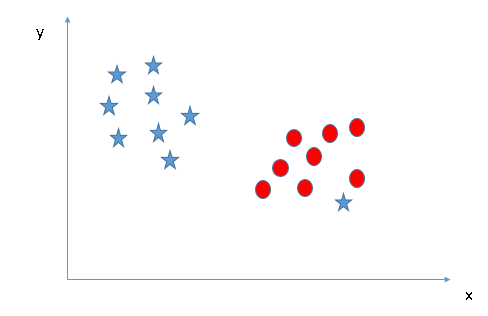  Como ya he mencionado, una estrella en el otro extremo es como un valor atípico para la clase de estrellas. El algoritmo SVM tiene una función para ignorar los valores atípicos y encontrar el hiperplano que tiene el margen máximo. Por lo tanto, podemos decir que la clasificación SVM es robusta a valores atípicos.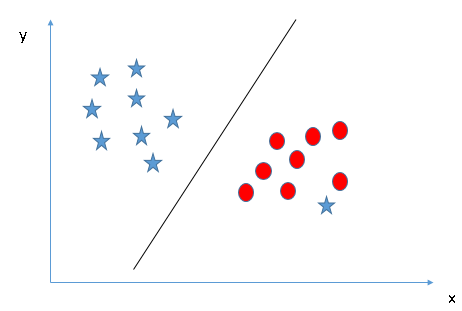
  
• Encuentre el hiperplano para segregar a las clases (Escenario-5): En el escenario siguiente, no podemos tener un hiperplano lineal entre las dos clases, entonces, ¿cómo clasifica SVM estas dos clases? Hasta ahora, solo hemos mirado el hiperplano lineal.
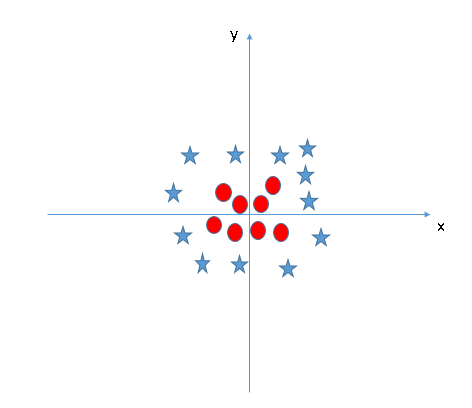  SVM puede resolver este problema. ¡Fácilmente! Resuelve este problema introduciendo una característica adicional. Aquí, agregaremos una nueva característica z = x ^ 2 + y ^ 2. Ahora, tracemos los puntos de datos en el eje xy z: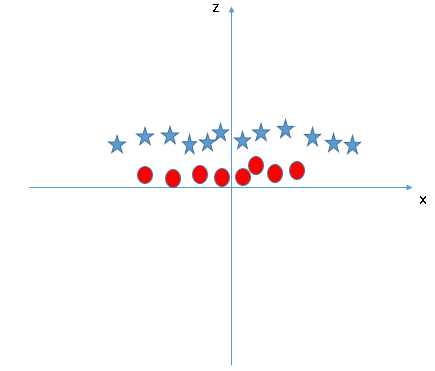
  
  En el gráfico anterior, los puntos a considerar son:
  • Todos los valores de z serían siempre positivos porque z es la suma al cuadrado de x e y
  • En el gráfico original, los círculos rojos aparecen cerca del origen de los ejes xey, lo que lleva a un valor más bajo de z y una estrella relativamente lejos del resultado del origen a un valor más alto de z.

  En el clasificador SVM, es fácil tener un hiperplano lineal entre estas dos clases. Pero, otra pregunta candente que surge es si necesitamos agregar esta función manualmente para tener un hiperplano. No, el algoritmo SVM tiene una técnica llamada núcleo truco. El kernel SVM es una función que toma un espacio de entrada de baja dimensión"Dimensión" es un término que se utiliza en diversas disciplinas, como la física, la matemática y la filosofía. Se refiere a la medida en la que un objeto o fenómeno puede ser analizado o descrito. En física, por ejemplo, se habla de dimensiones espaciales y temporales, mientras que en matemáticas puede referirse a la cantidad de coordenadas necesarias para representar un espacio. Su comprensión es fundamental para el estudio y... y lo transforma en un espacio de mayor dimensión, es decir, convierte un problema no separable en un problema separable. Es sobre todo útil en problemas de separación no lineal. En pocas palabras, realiza algunas transformaciones de datos extremadamente complejas, luego descubre el proceso para separar los datos en función de las etiquetas o salidas que ha definido.

  Cuando miramos el hiperplano en el espacio de entrada original, parece un círculo:
  

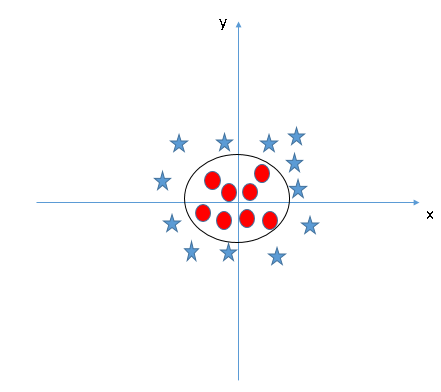
Ahora, veamos los métodos para aplicar el algoritmo clasificador SVM en un desafío de ciencia de datos.

También puede aprender sobre el funcionamiento de Support Vector Machine en formato de video de este Certificación de aprendizaje automático.

¿Cómo implementar SVM en Python y R?

En Python, scikit-learn es una biblioteca ampliamente utilizada para implementar algoritmos de aprendizaje automático. SVM también está disponible en la biblioteca scikit-learn y seguimos la misma estructura para usarlo (biblioteca de importación, creación de objetos, modelo de ajuste y predicción).

Ahora, echemos un vistazo a una declaración de problema de la vida real y un conjunto de datos para comprender cómo aplicar SVM para la clasificación.

Planteamiento del problema

La empresa Dream Housing Finance se ocupa de todos los préstamos hipotecarios. Tienen presencia en todas las áreas urbanas, semiurbanas y rurales. Un cliente primero solicita un préstamo hipotecario, luego de que la empresa valida la elegibilidad del cliente para un préstamo.

La empresa desea automatizar el proceso de elegibilidad del préstamo (en tiempo real) según los detalles del cliente proporcionados al completar un formulario de solicitud en línea. Estos detalles son género, estado civil, educación, número de dependientes, ingresos, monto del préstamo, historial crediticio y otros. Para automatizar este proceso, han dado un problema para identificar los segmentos de clientes, que son elegibles para el monto del préstamo para que puedan dirigirse específicamente a estos clientes. Aquí han proporcionado un conjunto de datos parcial.

Utilice la ventana de codificación a continuación para predecir la elegibilidad del préstamo en el conjunto de prueba. Intente cambiar los hiperparámetros de la SVM lineal para mejorar la precisión.

Soporte de código de máquina vectorial (SVM) en R

El paquete e1071 en R se utiliza para crear máquinas de vectores de soporte con facilidad. Tiene funciones auxiliares, así como código para el Clasificador Naive Bayes. La creación de una máquina de vectores de soporte en R y Python sigue enfoques similares, echemos un vistazo ahora al siguiente código:

#Import Library
require(e1071) #Contains the SVM 
Train <- read.csv(file.choose())
Test <- read.csv(file.choose())
# there are various options associated with SVM training; like changing kernel, gamma and C value.

# create model
model <- svm(Target~Predictor1+Predictor2+Predictor3,data=Train,kernel="linear",gamma=0.2,cost=100)

#Predict Output
preds <- predict(model,Test)
table(preds)

¿Cómo ajustar los parámetros de SVM?

El ajuste de los valores de los parámetros para los algoritmos de aprendizaje automático mejora eficazmente el rendimiento del modelo. Veamos la lista de parámetros disponibles con SVM.

sklearn.svm.SVC(C=1.0, kernel="rbf", degree=3, gamma=0.0, coef0=0.0, shrinking=True, probability=False,tol=0.001, cache_size=200, class_weight=None, verbose=False, max_iter=-1, random_state=None)

Voy a discutir sobre algunos parámetros importantes que tienen un mayor impacto en el rendimiento del modelo, «kernel», «gamma» y «C».

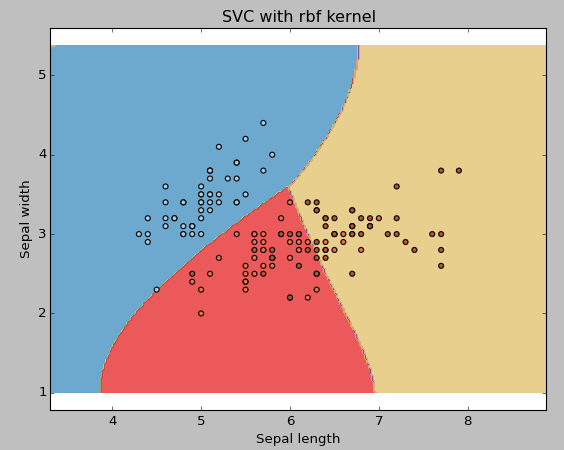
núcleo: Ya lo hemos discutido. Aquí, tenemos varias opciones disponibles con kernel como, «linear», «rbf», «poly» y otras (el valor predeterminado es «rbf»). Aquí «rbf» y «poly» son útiles para hiperplanos no lineales. Veamos el ejemplo, donde hemos usado kernel lineal en dos características del conjunto de datos de iris para clasificar su clase.

Admite código de máquina vectorial (SVM) en Python

Ejemplo: Tener un kernel SVM lineal

import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm, datasets

# import some data to play with
iris = datasets.load_iris()
X = iris.data[:, :2] # we only take the first two features. We could
 # avoid this ugly slicing by using a two-dim dataset
y = iris.target

# we create an instance of SVM and fit out data. We do not scale our
# data since we want to plot the support vectors
C = 1.0 # SVM regularization parameter
svc = svm.SVC(kernel="linear", C=1,gamma=0).fit(X, y)

# create a mesh to plot in
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
h = (x_max / x_min)/100
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
 np.arange(y_min, y_max, h))

plt.subplot(1, 1, 1)
Z = svc.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=plt.cm.Paired, alpha=0.8)

plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(xx.min(), xx.max())
plt.title('SVC with linear kernel')
plt.show()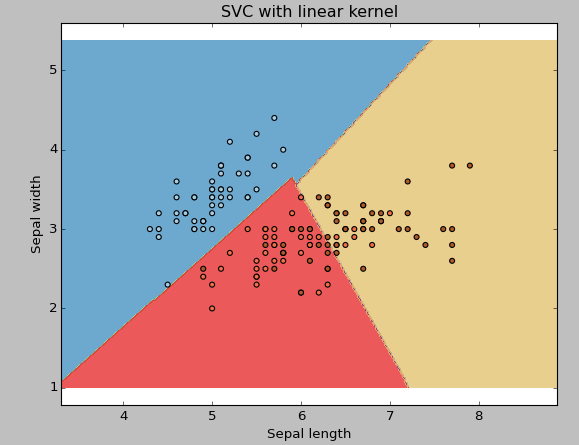

Ejemplo: Utilice el kernel SVM rbf

Cambie el tipo de kernel a rbf en la línea de abajo y observe el impacto.

svc = svm.SVC(kernel="rbf", C=1,gamma=0).fit(X, y)

Le sugiero que opte por el kernel SVM lineal si tiene una gran cantidad de características (> 1000) porque es más probable que los datos se puedan separar linealmente en un espacio de alta dimensión. Además, puede utilizar RBF, pero no olvide realizar una validación cruzada de sus parámetros para evitar un ajuste excesivo.

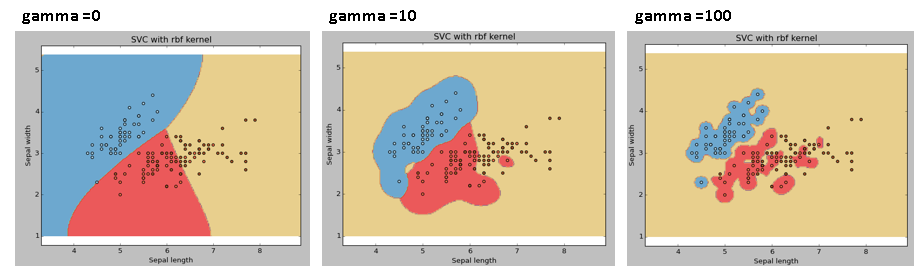
gama: Coeficiente de kernel para ‘rbf’, ‘poli’ y ‘sigmoide’. Cuanto más alto sea el valor de gamma, se intentará ajustar con exactitud el conjunto de datos de entrenamientoEl entrenamiento es un proceso sistemático diseñado para mejorar habilidades, conocimientos o capacidades físicas. Se aplica en diversas áreas, como el deporte, la educación y el desarrollo profesional. Un programa de entrenamiento efectivo incluye la planificación de objetivos, la práctica regular y la evaluación del progreso. La adaptación a las necesidades individuales y la motivación son factores clave para lograr resultados exitosos y sostenibles en cualquier disciplina...., es decir, el error de generalización y provocará un problema de sobreajuste.

Ejemplo: Vamos a diferenciar si tenemos gamma diferentes valores de gamma como 0, 10 o 100.

svc = svm.SVC(kernel="rbf", C=1,gamma=0).fit(X, y)

C: Parámetro de penalización C del término de error. También controla la compensación entre los límites de decisión suaves y la clasificación correcta de los puntos de entrenamiento.

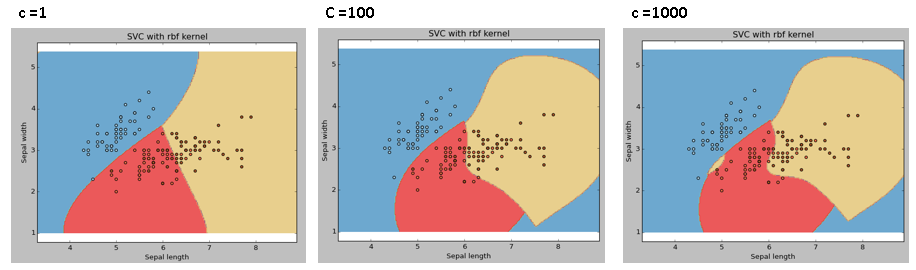
Siempre debemos mirar la puntuación de validación cruzada para tener una combinación efectiva de estos parámetros y evitar un ajuste excesivo.

En R, las SVM se pueden ajustar de manera similar a como lo están en Python. A continuación se mencionan los parámetros respectivos para el paquete e1071:

• El parámetro del kernel se puede ajustar para que tome «Linear», «Poly», «rbf», etc.
• El valor de gamma se puede ajustar configurando el parámetro «Gamma».
• El valor C en Python se ajusta mediante el parámetro «Costo» en R.

Pros y contras asociados con SVM

• Pros:
  • Funciona muy bien con un claro margen de separación.
  • Es eficaz en espacios de gran dimensión.
  • Es eficaz en los casos en que el número de dimensiones es mayor que el número de muestras.
  • Utiliza un subconjunto de puntos de entrenamiento en la función de decisión (llamados vectores de soporte), por lo que también es eficiente en la memoria.
• Contras:
  • No funciona bien cuando tenemos un gran conjunto de datos porque el tiempo de entrenamiento requerido es mayor
  • Tampoco funciona muy bien cuando el conjunto de datos tiene más ruido, es decir, las clases de destino se superponen
  • SVM no proporciona directamente estimaciones de probabilidad, estas se calculan mediante una costosa validación cruzada de cinco veces. Está incluido en el método SVC relacionado de la biblioteca scikit-learn de Python.

Problema de práctica

Encuentre la característica adicional adecuada para tener un hiperplano para segregar las clases en la siguiente instantánea:

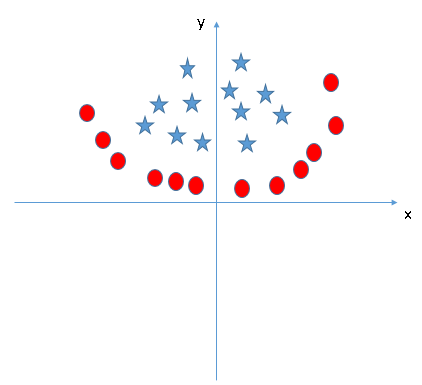
Responda el nombre de la variableEn estadística y matemáticas, una "variable" es un símbolo que representa un valor que puede cambiar o variar. Existen diferentes tipos de variables, como las cualitativas, que describen características no numéricas, y las cuantitativas, que representan cantidades numéricas. Las variables son fundamentales en experimentos y estudios, ya que permiten analizar relaciones y patrones entre diferentes elementos, facilitando la comprensión de fenómenos complejos.... en la sección de comentarios a continuación. Entonces revelaré la respuesta.

Notas finales

En este artículo, analizamos en detalle el algoritmo de aprendizaje automático, Support Vector Machine. Hablé sobre su concepto de trabajo, el proceso de implementación en python, los trucos para hacer eficiente el modelo ajustando sus parámetros, Pros y Contras, y finalmente un problema a resolver. Le sugiero que use SVM y analice la potencia de este modelo ajustando los parámetros. También quiero escuchar su experiencia con SVM, ¿cómo ha ajustado los parámetros para evitar un ajuste excesivo y reducir el tiempo de entrenamiento?

¿Le ha resultado útil este artículo? Comparta sus opiniones / pensamientos en la sección de comentarios a continuación.

Si le gusta lo que acaba de leer y desea continuar con su aprendizaje sobre análisis, suscríbete a nuestros correos electrónicos, Síguenos en Twitter o como nuestro pagina de Facebook.

Relacionado