Introducción
Usamos frecuentemente el término Probabilidad pero no se dé cuenta de lo poderoso que es este concepto. En términos simples, la probabilidad es la probabilidad de que suceda algo. Y uno de los conceptos fundamentales de probabilidad son los axiomas de probabilidad, que son esenciales para la estadística y el análisis de datos exploratorios.
Los axiomas significan una regla, un principio que la mayoría de la gente cree que es cierto. Es la premisa sobre la base de la cual hacemos un mayor razonamiento
En este artículo, cubriré los tres axiomas de probabilidad en detalle.
Nota: Si está más interesado en aprender conceptos en un formato audiovisual, tenemos este artículo completo explicado en el video a continuación. Si no es así, puede seguir leyendo.
Axiomas de probabilidad
Hay tres axiomas de probabilidad que constituyen la base de la teoría de la probabilidad:
Axioma 1: Probabilidad de evento
La primera es que la probabilidad de un evento siempre está entre 0 y 1. 1 indica una acción definida de cualquiera de los resultados de un evento y 0 indica que no es posible un resultado del evento.
Axioma 2: Probabilidad del espacio muestral
Para el espacio muestral, la probabilidad de todo el espacio muestral es 1.
Axioma 3: Eventos mutuamente excluyentes
Y el tercero es: la probabilidad de que el evento contenga cualquier resultado posible de dos mutuamente disjuntos es la suma de su probabilidad individual.
¡Ahora veamos cada uno de ellos en detalle!
1. Probabilidad del evento
El primer axioma de probabilidad es que la probabilidad de cualquier evento está entre 0 y 1.
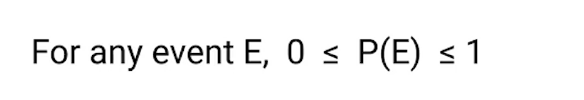
Como sabemos, la fórmula de probabilidad es que dividimos el número total de resultados en el evento por el número total de resultados en el espacio muestral.

Y el evento es un subconjunto del espacio muestral, por lo que el evento no puede tener más resultados que el espacio muestral. Claramente, este valor va a estar entre 0 y 1 ya que el denominador siempre es mayor que el numerador.
2. Probabilidad del espacio muestral
El segundo axioma es que la probabilidad de todo el espacio muestral es igual a 1.

Tomemos un ejemplo del conjunto de datos. Supongamos que tenemos que averiguar la probabilidad de que las clientas se muevan por su tipo de ocupación.
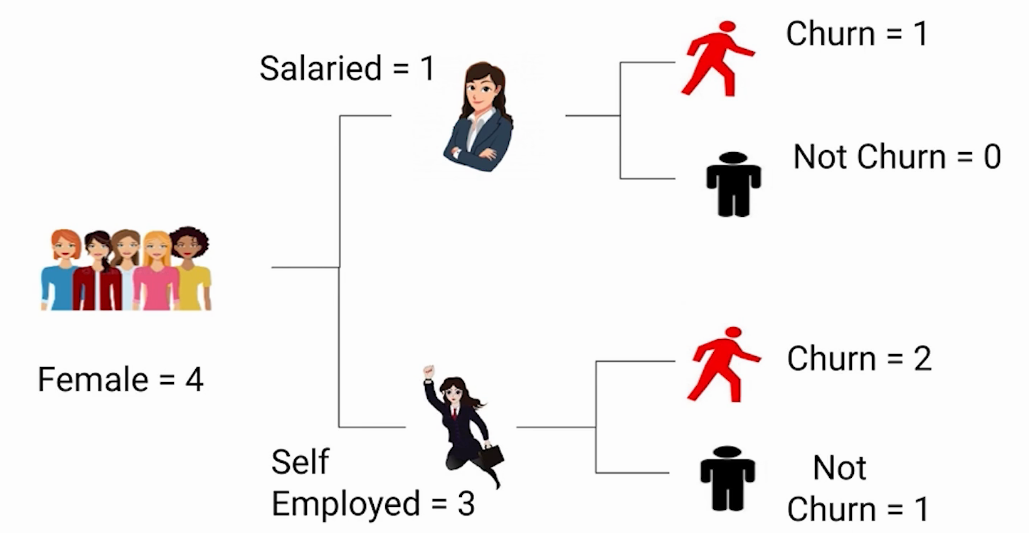
En nuestro conjunto de datos, tenemos 4 clientas, una de ellas asalariada y tres de ellas autónomas. La mujer asalariada se va a batir. Como solo tenemos una mujer asalariada que va a abandonar, el número de clientas asalariadas que no van a abandonar es 0. Entre las 3 clientas autónomas, dos van a abandonar y podemos ver que una es autónoma la hembra no se va a batir. Este es el conjunto de datos completo:
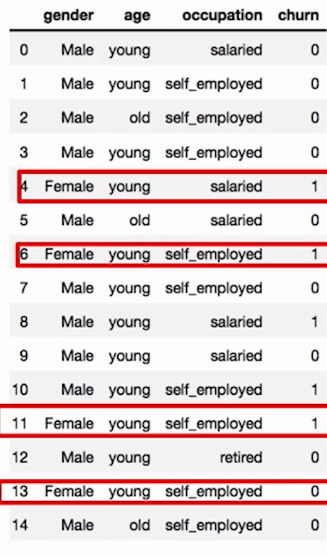
Entonces, la probabilidad del estado agitado de una clienta por profesión, en el espacio muestral del problema, en realidad tenemos:
Churn asalariado, sueldo no churn, churn por cuenta propia, churn por cuenta propia, no churn
Y como comentamos su distribución anteriormente, en este espacio de muestra de clienta:
Rotación asalariada = 1
Asalariado No abandono = 0
Churn de autónomos = 2
Trabajador por cuenta propia No abandono = 1
Si tuviera que averiguar la probabilidad de que una persona que es mujer reciba un salario y esté batiendo, sería igual a:
![]()
De manera similar, la probabilidad de que no se pierda el salario es:
![]()
Luego tenemos el Churn de autónomos:
![]()
Y, finalmente, autónomos que no abandonan:

Y si los sumamos todos obtenemos 1:
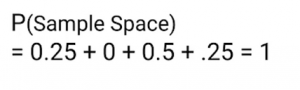
Básicamente, decir que este es nuestro espacio muestral completo y que la probabilidad total de que lleguemos aquí es igual a 1. Esto nos lleva al axioma 3, que está relacionado con eventos mutuamente excluyentes.
3. Evento mutuamente exclusivo

Si recuerda la fórmula de unión, recordará que el término de intersección no está aquí, lo que significa que no hay nada en común entre A y B. Entendamos este tipo particular de eventos que se llama Eventos mutuamente excluyentes.
Estos eventos mutuamente excluyentes significan que dichos eventos no pueden ocurrir juntos o, en otras palabras, no tienen valores comunes o podemos decir que su intersección es cero / nula. También podemos representar tales eventos de la siguiente manera:
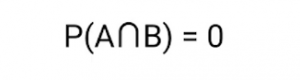
Esto significa que la intersección es cero o no tienen ningún valor común. Por ejemplo, si el
Evento A: obtiene un número mayor que 4 después de lanzar un dado, los posibles resultados serían 5 y 6.

Incluso B: obtiene un número menor que 3 al lanzar un dado. Aquí los posibles resultados serían 1 y 2.

Claramente, estos dos eventos no pueden tener un resultado común. Una cosa interesante a tener en cuenta aquí es que los eventos A y B no se complementan entre sí, pero son mutuamente excluyentes.
Mutuamente exhaustivos
Un concepto más importante es Evento mutuamente exhaustivo que a menudo se confunde con eventos mutuamente inclusivos. Los eventos mutuamente exhaustivos significan que tales eventos juntos constituyen todo lo que posiblemente pueda suceder en un experimento aleatorio. Eso significa que la unión de estos eventos hace que el espacio muestral:
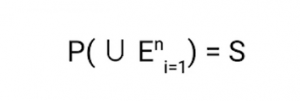
Entendamos esto con un ejemplo:
Evento A: Obtener un número mayor que 2 después de un dado, los posibles resultados serían:

Evento B: Obtener un número menor que 4 después de lanzar un dado. Aquí los posibles resultados serían:

Claramente, estos dos eventos juntos constituyen todos los resultados que pueden tener lugar después de lanzar un dado.
¿En qué se diferencian los eventos mutuamente exhaustivos de los eventos mutuamente excluyentes?
En el ejemplo anterior, obteniendo un numero 3 fue común entre ambos eventos. Por lo tanto, estos NO PUEDEN ser mutuamente excluyentes, pero definitivamente son mutuamente exhaustivos. Por otro lado, si tenemos otro evento:
Evento C: Obtener un número menor que 3 después de lanzar un dado, los posibles resultados serían:

Ahora podemos decir que el Evento A y el Evento C son mutuamente excluyentes ya que no tienen nada en común.
Notas finales
En este artículo, cubrimos los axiomas de probabilidad y la diferencia entre eventos mutuamente excluyentes y mutuamente exhaustivos.
Si está buscando comenzar su viaje de ciencia de datos y desea todos los temas bajo un mismo techo, su búsqueda se detiene aquí. Eche un vistazo a la IA y ML BlackBelt certificadas de DataPeaker Más Programa
¡Háganos saber en los comentarios si tiene alguna consulta!






