Este artículo fue publicado como parte del Blogatón de ciencia de datos.
Introducción
¡APRIETE PARA EL IMPACTO! ¡ABRAZADERA! ¡ABRAZADERA! ¡ABRAZADERA!
¡¡¡UPS!!! Nuestro avión se ha estrellado, pero afortunadamente todos estamos a salvo. Somos científicos de datos, por lo que queremos abrir la caja negra y ver qué cosas aleatorias se han registrado en su interior. Sí, pasemos a nuestro tema.
¿Qué son los bosques aleatorios?
Debes haber resuelto al menos una vez un problema de probabilidad en tu escuela secundaria en el que se suponía que debías encontrar la probabilidad de obtener una bola de un color específico de una bolsa que contiene bolas de diferentes colores, dada la cantidad de bolas de cada color. Los bosques aleatorios son simples si tratamos de aprenderlos con esta analogía en mente.
Los bosques aleatorios (RF) son básicamente una bolsa que contiene n árboles de decisión (DT) que tienen un conjunto diferente de hiperparámetros y se entrenan en diferentes subconjuntos de datos. ¡Digamos que tengo 100 árboles de decisión en mi bolsa de bosque aleatorio! Como acabo de decir, estos árboles de decisión tienen un conjunto diferente de hiperparámetros y un subconjunto diferente de datos de entrenamientoEl entrenamiento es un proceso sistemático diseñado para mejorar habilidades, conocimientos o capacidades físicas. Se aplica en diversas áreas, como el deporte, la educación y el desarrollo profesional. Un programa de entrenamiento efectivo incluye la planificación de objetivos, la práctica regular y la evaluación del progreso. La adaptación a las necesidades individuales y la motivación son factores clave para lograr resultados exitosos y sostenibles en cualquier disciplina...., por lo que la decisión o la predicción dada por estos árboles puede variar mucho. Consideremos que de alguna manera he entrenado todos estos 100 árboles con su respectivo subconjunto de datos. Ahora les preguntaré a los cien árboles en mi bolso cuál es su predicción sobre mis datos de prueba. Ahora solo necesitamos tomar una decisión sobre un ejemplo o un dato de prueba, lo hacemos mediante un simple voto. Seguimos lo que la mayoría de los árboles han predicho para ese ejemplo.
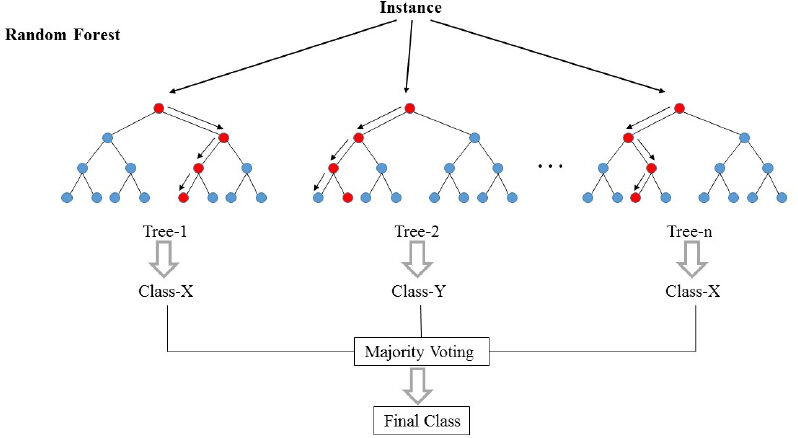
En la imagen de arriba, podemos ver cómo se clasifica un ejemplo usando n árboles donde la predicción final se realiza tomando un voto de todos los n árboles.
En el lenguaje de aprendizaje automático, las RF también se denominan método de ensamble o ensacado. ¡Creo que la palabra embolsar podría provenir de la analogía que acabamos de discutir!
¡¡Acerquémonos un poco más a ML Jargons !!
El bosque aleatorio es básicamente un algoritmo de aprendizaje supervisadoEl aprendizaje supervisado es un enfoque de machine learning donde un modelo se entrena utilizando un conjunto de datos etiquetados. Cada entrada en el conjunto de datos está asociada a una salida conocida, lo que permite al modelo aprender a predecir resultados para nuevas entradas. Este método es ampliamente utilizado en aplicaciones como la clasificación de imágenes, el reconocimiento de voz y la predicción de tendencias, destacando su importancia en.... Esto se puede utilizar tanto para tareas de regresión como de clasificación. Pero discutiremos su uso para la clasificación porque es más intuitivo y fácil de entender. El bosque aleatorio es uno de los algoritmos más utilizados por su simplicidad y estabilidad.
Mientras se construyen subconjuntos de datos para árboles, la palabra «aleatorio» entra en escena. Se crea un subconjunto de datos seleccionando aleatoriamente x número de características (columnas) y y número de ejemplos (filas) del conjunto de datos original de n características ym ejemplos.
Los bosques aleatorios son más estables y confiables que solo un árbol de decisiones. Esto es simplemente decir que es mejor votar por todos los ministros del gabinete en lugar de simplemente aceptar la decisión dada por el primer ministro.
Como hemos visto que los bosques aleatorios no son más que la colección de árboles de decisiones, se vuelve esencial conocer el árbol de decisiones. Así que profundicemos en los árboles de decisiones.
¿Qué es un árbol de decisiones?
En palabras muy simples, es un «conjunto de reglas» creado mediante el aprendizaje de un conjunto de datos que se puede utilizar para hacer predicciones sobre datos futuros. Intentaremos entender esto con un ejemplo.
Aquí se muestra un pequeño conjunto de datos simple. En este conjunto de datos, las primeras cuatro características son características independientes y la última son las características dependientes. Las características independientes describen las condiciones climáticas en un día determinado y la característica dependiente nos dice si pudimos jugar al tenis ese día o no.
Ahora intentaremos crear algunas reglas usando características independientes para predecir características dependientes. Solo por observación, podemos ver que si Outlook está nublado, el juego siempre es sí, independientemente de otras características. De manera similar, podemos crear todas las reglas para describir completamente el conjunto de datos. Aquí están todas las reglas.
- R1: Si (Outlook = Soleado) Y (Humedad = Alta) Entonces Juega = No
- R2: Si (Outlook = Soleado) Y (Humedad = Normal) Entonces Juega = Sí
- R3: Si (Outlook = Nublado) Entonces Reproducir = Sí
- R4: Si (Outlook = Lluvia) Y (Viento = Fuerte) Entonces Juega = No
- R5: Si (Perspectiva = Lluvia) Y (Viento = Débil) Entonces Pague = Sí
Podemos convertir fácilmente estas reglas en un diagrama de árbol. Aquí está el gráfico de árbol.
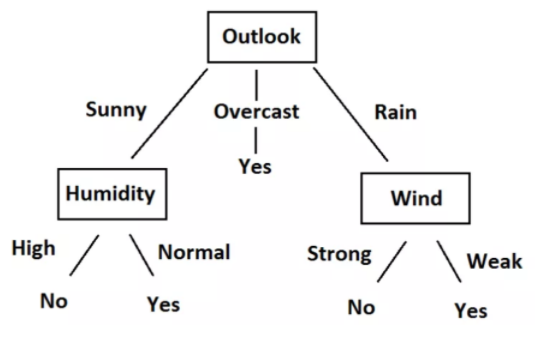
Al observar los datos, las reglas y el árbol, comprenderá que ahora podemos predecir si debemos jugar al tenis o no, dada la situación del clima en función de características independientes. Todo este proceso de creación de reglas para un dato dado no es más que el entrenamiento del modelo de árbol de decisión.
Podríamos establecer reglas y hacer un árbol con solo observar aquí porque el conjunto de datos es muy pequeño. Pero, ¿cómo entrenamos el árbol de decisiones en un conjunto de datos más grande? Para eso, necesitamos saber un poco de matemáticas. Ahora intentaremos comprender las matemáticas detrás del árbol de decisiones.
Conceptos matemáticos detrás del árbol de decisiones
Esta sección consta de dos conceptos importantes: Entropía y Ganancia de información.
Entropía
La entropía es una medidaLa "medida" es un concepto fundamental en diversas disciplinas, que se refiere al proceso de cuantificar características o magnitudes de objetos, fenómenos o situaciones. En matemáticas, se utiliza para determinar longitudes, áreas y volúmenes, mientras que en ciencias sociales puede referirse a la evaluación de variables cualitativas y cuantitativas. La precisión en la medición es crucial para obtener resultados confiables y válidos en cualquier investigación o aplicación práctica.... de la aleatoriedad de un sistema. La entropía del espacio muestral S es el número esperado de bits necesarios para codificar la clase de un miembro de S extraído al azar. Aquí tenemos 14 filas en nuestros datos, por lo que 14 miembros.
Entropía E (S) = -∑p (x) * log2(p (x))
La entropía del sistema se calcula mediante la fórmula anterior, donde p (x) es la probabilidad de obtener la clase x de esos 14 miembros. Tenemos dos clases aquí, una es Sí y la otra es No en la columna Reproducir. Tenemos 9 Sí y 5 No en nuestro conjunto de datos. Entonces, el cálculo de la entropía aquí será el siguiente
E (S) = -[p(Yes)*log(p(Yes))+ p(No)*log(p(No))]= -[(9/14)*log((9/14))+ (5/14*log((5/14)))]= 0,94
Ganancia de información
La ganancia de información es la cantidad en la que se reduce la Entropía del sistema debido a la división que hemos realizado. Hemos creado el árbol usando observaciones. Pero, ¿cómo es que decidimos que primero deberíamos dividir los datos en función de Outlook y no en ninguna otra función? La razón es que esta división estaba reduciendo la entropía en la cantidad máxima, pero lo hicimos intuitivamente en el ejemplo anterior.
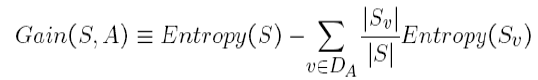
La división del árbol de arriba nos muestra que 9 SÍ y 5 No se han dividido como (2 Y, 3 N), (4 Y, 0 N), (3 Y, 2 N), cuando hacemos la división según la perspectiva. Los valores de E debajo de cada división muestran valores de entropía considerándose a sí mismos como un sistema completo y usando la fórmula de entropía anterior. Luego, hemos calculado la ganancia de información para la división de perspectivas utilizando la fórmula de ganancia anterior.
De manera similar, podemos calcular la ganancia de información para cada división de características de forma independiente. Y obtenemos los siguientes resultados:
- Ganancia (S, Outlook) = 0,247
- Ganancia (S, humedad) = 0,151
- Ganancia (S, viento) = 0.048
- Ganancia (S, temperatura) = 0.029
Podemos ver que estamos obteniendo la máxima ganancia de información al dividir la función de Outlook. Repetimos este procedimiento para crear todo el árbol. Espero que hayas disfrutado leyendo el artículo. Si le gusta el artículo, compártalo con sus colegas y amigos. ¡¡¡Feliz lectura!!!
