Este artículo fue publicado como parte del Blogatón de ciencia de datos
¡Hola chicos! En este blog, voy a discutir todo sobre la clasificación de imágenes.
En los últimos años, Deep Learning ha demostrado que es una herramienta muy poderosa debido a su capacidad para manejar grandes cantidades de datos. El uso de capas ocultas supera las técnicas tradicionales, especialmente para el reconocimiento de patrones. Una de las redes neuronales profundas más populares son las redes neuronales convolucionales (CNN).
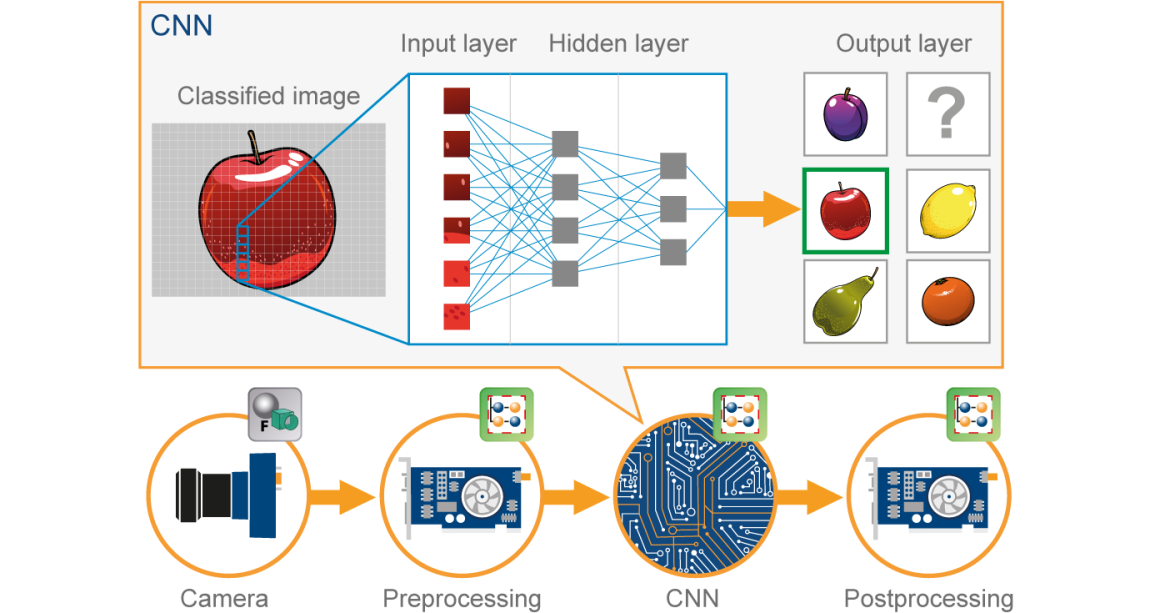
Una red neuronal convolucionalLas redes neuronales convolucionales (CNN) son un tipo de arquitectura de red neuronal diseñadas especialmente para el procesamiento de datos con una estructura de cuadrícula, como imágenes. Utilizan capas de convolución para extraer características jerárquicas, lo que las hace especialmente efectivas en tareas de reconocimiento de patrones y clasificación. Gracias a su capacidad para aprender de grandes volúmenes de datos, las CNN han revolucionado campos como la visión por computadora... (CNN) es un tipo de Red neuronalLas redes neuronales son modelos computacionales inspirados en el funcionamiento del cerebro humano. Utilizan estructuras conocidas como neuronas artificiales para procesar y aprender de los datos. Estas redes son fundamentales en el campo de la inteligencia artificial, permitiendo avances significativos en tareas como el reconocimiento de imágenes, el procesamiento del lenguaje natural y la predicción de series temporales, entre otros. Su capacidad para aprender patrones complejos las hace herramientas poderosas... artificial (ANN) utilizado en el reconocimiento y procesamiento de imágenes, que está especialmente diseñado para procesar datos (píxeles).
Fuente de la imagen: Google.com
Antes de seguir adelante, debemos comprender qué es la red neuronal. Vamos…
Red neuronal:
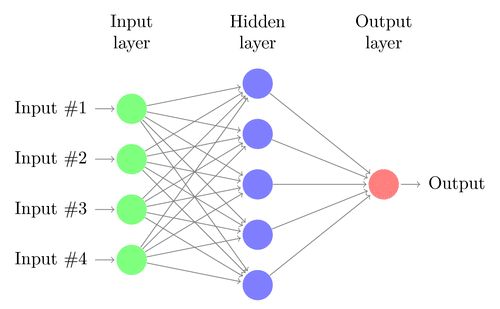
Una red neuronal se construye a partir de varios nodos interconectados llamados «Neuronas». Las neuronas están dispuestas en capa de entradaLa "capa de entrada" se refiere al nivel inicial en un proceso de análisis de datos o en arquitecturas de redes neuronales. Su función principal es recibir y procesar la información bruta antes de que esta sea transformada por capas posteriores. En el contexto de machine learning, una adecuada configuración de la capa de entrada es crucial para garantizar la efectividad del modelo y optimizar su rendimiento en tareas específicas...., capa oculta y capa de salidaLa "capa de salida" es un concepto utilizado en el ámbito de la tecnología de la información y el diseño de sistemas. Se refiere a la última capa de un modelo de software o arquitectura que se encarga de presentar los resultados al usuario final. Esta capa es crucial para la experiencia del usuario, ya que permite la interacción directa con el sistema y la visualización de datos procesados..... La capa de entrada corresponde a nuestros predictores / características y la capa de salida a nuestras variables de respuesta.
Fuente de la imagen: Google.com
Perceptrón multicapa (MLP):
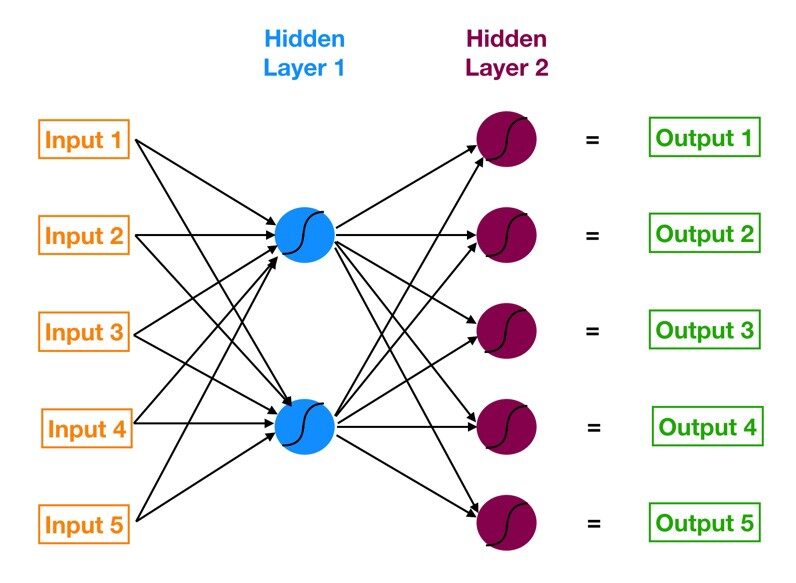
La red neuronal con una capa de entrada, una o más capas ocultas y una capa de salida se llama perceptrón multicapa (MLP). MLP es inventado por Frank Rosenblatt en el año de 1957. MLP que se muestra a continuación tiene 5 nodos de entrada, 5 nodos ocultos con dos capas ocultas y un nodoNodo es una plataforma digital que facilita la conexión entre profesionales y empresas en busca de talento. A través de un sistema intuitivo, permite a los usuarios crear perfiles, compartir experiencias y acceder a oportunidades laborales. Su enfoque en la colaboración y el networking hace de Nodo una herramienta valiosa para quienes desean expandir su red profesional y encontrar proyectos que se alineen con sus habilidades y objetivos.... de salida
Fuente de la imagen: Google.com
¿Cómo funciona esta red neuronal?
– Las neuronas de la capa de entrada reciben información entrante de los datos que procesan y distribuyen al capas ocultas.
– Esa información, a su vez, es procesada por capas ocultas y se pasa a la salida. neuronas.
– La información de esta red neuronal artificial (ANN) se procesa en términos de una función de activaciónLa función de activación es un componente clave en las redes neuronales, ya que determina la salida de una neurona en función de su entrada. Su propósito principal es introducir no linealidades en el modelo, permitiendo que aprenda patrones complejos en los datos. Existen diversas funciones de activación, como la sigmoide, ReLU y tanh, cada una con características particulares que afectan el rendimiento del modelo en diferentes aplicaciones..... Esta función en realidad imita a las neuronas del cerebro.
– Cada neurona contiene un valor de funciones de activación y un valor umbral.
– Los valor umbral es el valor mínimo que debe poseer la entrada para que pueda ser activada.
– La tarea de la neurona es realizar una suma ponderada de todas las señales de entrada y aplicar la función de activación sobre la suma antes de pasarla a la siguiente capa (oculta o de salida).
Entendamos qué es la suma de ponderación.
Digamos que tenemos valores 𝑎1, 𝑎2, 𝑎3, 𝑎4 para la entrada y pesos como 𝑤1, 𝑤2, 𝑤3, 𝑤4 como la entrada a una de las neuronas de la capa oculta, digamos 𝑛𝑗, entonces la suma ponderada se representa como
𝑆𝑗 = σ 𝑖 = 1to4 𝑤𝑖 * 𝑎𝑖 + 𝑏𝑗
donde 𝑏𝑗: sesgo debido al nodo
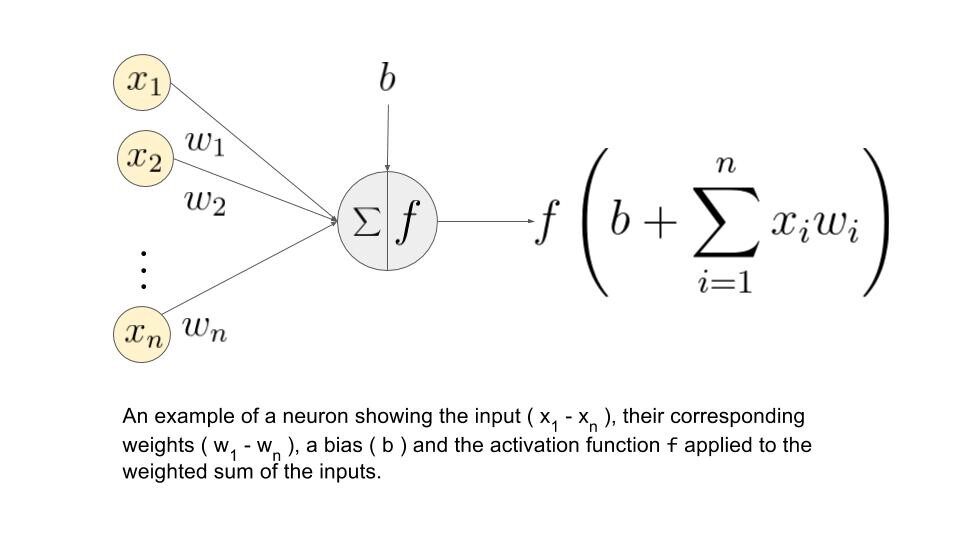
Fuente de la imagen: Google.com
¿Cuáles son las funciones de activación?
Estas funciones son necesarias para introducir una no linealidad en la red. Se aplica la función de activación y esa salida se pasa a la siguiente capa.
* Posibles funciones *
• Sigmoide: la función sigmoidea es diferenciable. Produce una salida entre 0 y 1.
• Tangente hiperbólica: La tangente hiperbólica también es diferenciable. Esto produce una salida entre -1 y 1.
• ReLULa función de activación ReLU (Rectified Linear Unit) es ampliamente utilizada en redes neuronales debido a su simplicidad y eficacia. Definida como ( f(x) = max(0, x) ), ReLU permite que las neuronas se activen solo cuando la entrada es positiva, lo que contribuye a mitigar el problema del desvanecimiento del gradiente. Su uso ha demostrado mejorar el rendimiento en diversas tareas de aprendizaje profundo, haciendo de ReLU una opción...: ReLU es la función más popular. ReLU se usa ampliamente en el aprendizaje profundoEl aprendizaje profundo, una subdisciplina de la inteligencia artificial, se basa en redes neuronales artificiales para analizar y procesar grandes volúmenes de datos. Esta técnica permite a las máquinas aprender patrones y realizar tareas complejas, como el reconocimiento de voz y la visión por computadora. Su capacidad para mejorar continuamente a medida que se le proporcionan más datos la convierte en una herramienta clave en diversas industrias, desde la salud....
• Softmax: la función softmaxLa función softmax es una herramienta matemática utilizada en el campo del aprendizaje automático, especialmente en redes neuronales. Convierte un vector de valores en una distribución de probabilidad, asignando probabilidades a cada clase en problemas de clasificación múltiple. Su fórmula normaliza las salidas, asegurando que la suma de todas las probabilidades sea igual a uno, lo que permite interpretar los resultados de manera efectiva. Es fundamental en la optimización de... se utiliza para problemas de clasificación de clases múltiples. Es una generalización de la función sigmoidea. También produce una salida entre 0 y 1
Ahora, vayamos con nuestro tema CNN …
CNN:
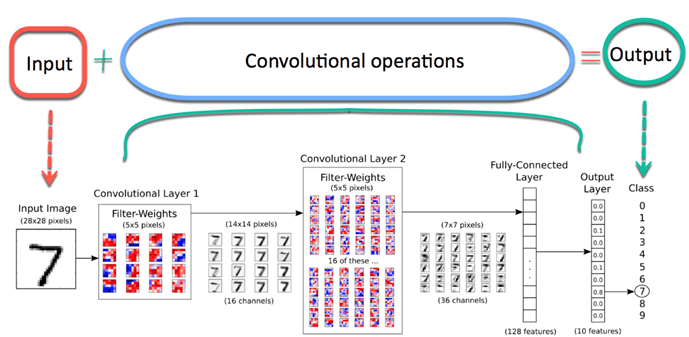
Ahora imagina que hay una imagen de un pájaro, y quieres identificarlo si realmente es un pájaro u otra cosa. Lo primero que debe hacer es alimentar los píxeles de la imagen en forma de matrices a la capa de entrada de la red neuronal (las redes MLP se utilizan para clasificar tales cosas). Las capas ocultas llevan la extracción de características mediante la realización de varios cálculos y operaciones. Hay varias capas ocultas como la convolución, el ReLU y la capa de agrupación que realiza la extracción de características de su imagen. Entonces, finalmente, hay una capa completamente conectada que puede ver que identifica el objeto exacto en la imagen. Puede comprender muy fácilmente en la siguiente figura"Figura" es un término que se utiliza en diversos contextos, desde el arte hasta la anatomía. En el ámbito artístico, se refiere a la representación de formas humanas o animales en esculturas y pinturas. En la anatomía, designa la forma y estructura del cuerpo. Además, en matemáticas, "figura" se relaciona con las formas geométricas. Su versatilidad hace que sea un concepto fundamental en múltiples disciplinas....:
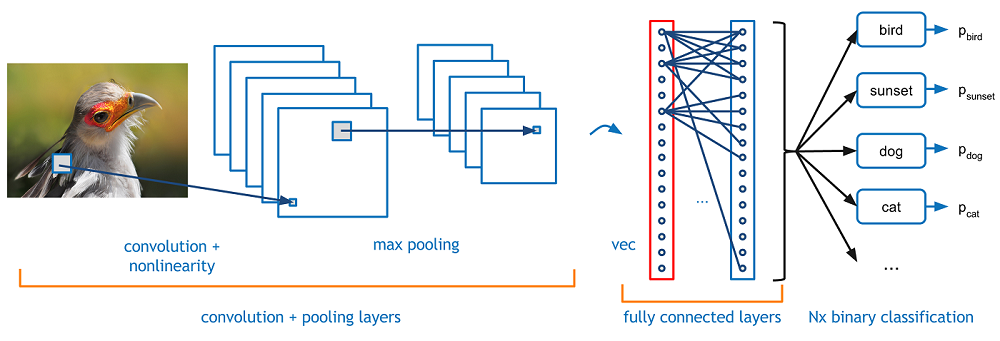
Fuente de la imagen: Google.com
Circunvolución:-
La operación de convolución implica operaciones aritméticas matriciales y cada imagen se representa en forma de una matriz de valores (píxeles).
Entendamos el ejemplo:
a = [2,5,8,4,7,9]
b = [1,2,3]
En la operación de convolución, las matrices se multiplican uno por uno en cuanto a elementos, y el producto se agrupa o suma para crear una nueva matriz que representa a * b.
Los primeros tres elementos de la matriz a ahora se multiplican por los elementos de la matriz B. El producto se suma para obtener el resultado y se almacena en una nueva matriz de a * b.
Este proceso permanece continuo hasta que se completa la operación.
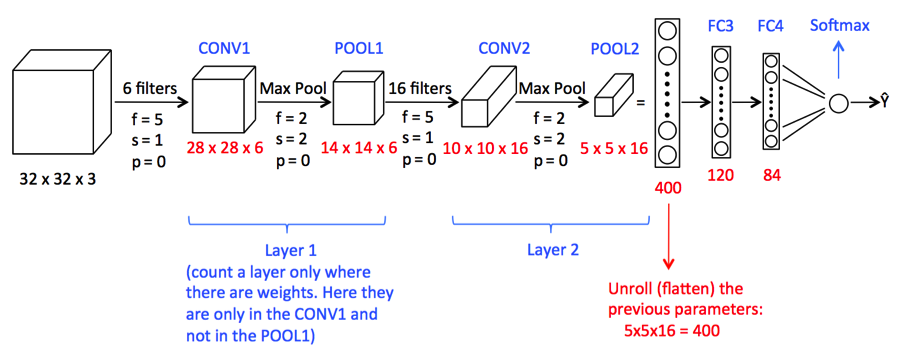
Fuente de la imagen: Google.com
Agrupación:
Después de la convolución, hay otra operación llamada agrupación. Entonces, en la cadena, la convolución y la agrupación se aplican secuencialmente en los datos con el fin de extraer algunas características de los datos. Después de las capas convolucionales y agrupadas secuenciales, los datos se aplanan
en una red neuronal de retroalimentación que también se llama perceptrón multicapa.
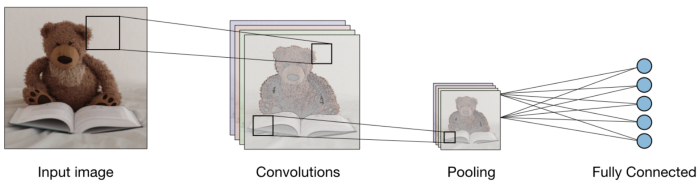
Fuente de la imagen: Google.com
Hasta este punto, hemos visto conceptos que son importantes para nuestro modelo de construcción de CNN.
Ahora avanzaremos para ver un estudio de caso de CNN.
1) Aquí vamos a importar las bibliotecas necesarias que se requieren para realizar tareas de CNN.
import NumPy as np %matplotlib inline import matplotlib.image as mpimg import matplotlib.pyplot as plt import TensorFlow as tf tf.compat.v1.set_random_seed(2019)
2) Aquí requerimos el siguiente código para formar el modelo CNN
model = tf.keras.models.Sequential([
tf.keras.layers.Conv2D(16,(3,3),activation = "relu" , input_shape = (180,180,3)) ,
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Conv2D(32,(3,3),activation = "relu") ,
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Conv2D(64,(3,3),activation = "relu") ,
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Conv2D(128,(3,3),activation = "relu"),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(550,activation="relu"), #Adding the Hidden layer
tf.keras.layers.Dropout(0.1,seed = 2019),
tf.keras.layers.Dense(400,activation ="relu"),
tf.keras.layers.Dropout(0.3,seed = 2019),
tf.keras.layers.Dense(300,activation="relu"),
tf.keras.layers.Dropout(0.4,seed = 2019),
tf.keras.layers.Dense(200,activation ="relu"),
tf.keras.layers.Dropout(0.2,seed = 2019),
tf.keras.layers.Dense(5,activation = "softmax") #Adding the Output Layer
])
Una imagen enrevesada puede ser demasiado grande y, por lo tanto, se reduce sin perder características o patrones, por lo que se realiza la agrupación.
Aquí, Crear una red neuronal es inicializar la red utilizando el modelo secuencial de Keras.
Aplanar (): el aplanamiento transforma una matriz bidimensional de características en un vector de características.
3) Ahora veamos un resumen del modelo de CNN
model.summary()
Imprimirá la siguiente salida
Model: "sequential" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= conv2d (Conv2D) (None, 178, 178, 16) 448 _________________________________________________________________ max_pooling2d (MaxPooling2D) (None, 89, 89, 16) 0 _________________________________________________________________ conv2d_1 (Conv2D) (None, 87, 87, 32) 4640 _________________________________________________________________ max_pooling2d_1 (MaxPooling2 (None, 43, 43, 32) 0 _________________________________________________________________ conv2d_2 (Conv2D) (None, 41, 41, 64) 18496 _________________________________________________________________ max_pooling2d_2 (MaxPooling2 (None, 20, 20, 64) 0 _________________________________________________________________ conv2d_3 (Conv2D) (None, 18, 18, 128) 73856 _________________________________________________________________ max_pooling2d_3 (MaxPooling2 (None, 9, 9, 128) 0 _________________________________________________________________ flatten (Flatten) (None, 10368) 0 _________________________________________________________________ dense (Dense) (None, 550) 5702950 _________________________________________________________________ dropout (Dropout) (None, 550) 0 _________________________________________________________________ dense_1 (Dense) (None, 400) 220400 _________________________________________________________________ dropout_1 (Dropout) (None, 400) 0 _________________________________________________________________ dense_2 (Dense) (None, 300) 120300 _________________________________________________________________ dropout_2 (Dropout) (None, 300) 0 _________________________________________________________________ dense_3 (Dense) (None, 200) 60200 _________________________________________________________________ dropout_3 (Dropout) (None, 200) 0 _________________________________________________________________ dense_4 (Dense) (None, 5) 1005 ================================================================= Total params: 6,202,295 Trainable params: 6,202,295 Non-trainable params: 0
4) Así que ahora estamos obligados a especificar optimizadores.
from tensorflow.keras.optimizers import RMSprop,SGD,Adam adam=Adam(lr=0.001) model.compile(optimizer="adam", loss="categorical_crossentropy", metrics = ['acc'])
El optimizador se usa para reducir el costo calculado por entropía cruzada
La función de pérdidaLa función de pérdida es una herramienta fundamental en el aprendizaje automático que cuantifica la discrepancia entre las predicciones del modelo y los valores reales. Su objetivo es guiar el proceso de entrenamiento al minimizar esta diferencia, permitiendo así que el modelo aprenda de manera más efectiva. Existen diferentes tipos de funciones de pérdida, como el error cuadrático medio y la entropía cruzada, cada una adecuada para distintas tareas y... se utiliza para calcular el error.
El término métricas se utiliza para representar la eficiencia del modelo.
5) En este paso, veremos cómo configurar el directorio de datos y generar datos de imagen.
bs=30 #Setting batch size
train_dir = "D:/Data Science/Image Datasets/FastFood/train/" #Setting training directory
validation_dir = "D:/Data Science/Image Datasets/FastFood/test/" #Setting testing directory
from tensorflow.keras.preprocessing.image import ImageDataGenerator
# All images will be rescaled by 1./255.
train_datagen = ImageDataGenerator( rescale = 1.0/255. )
test_datagen = ImageDataGenerator( rescale = 1.0/255. )
# Flow training images in batches of 20 using train_datagen generator
#Flow_from_directory function lets the classifier directly identify the labels from the name of the directories the image lies in
train_generator=train_datagen.flow_from_directory(train_dir,batch_size=bs,class_mode="categorical",target_size=(180,180))
# Flow validation images in batches of 20 using test_datagen generator
validation_generator = test_datagen.flow_from_directory(validation_dir,
batch_size=bs,
class_mode="categorical",
target_size=(180,180))
La salida será:
Found 1465 images belonging to 5 classes. Found 893 images belonging to 5 classes.
6) Paso final del modelo de ajuste.
history = model.fit(train_generator,
validation_data=validation_generator,
steps_per_epoch=150 // bs,
epochs=30,
validation_steps=50 // bs,
verbose=2)
La salida será:
Epoch 1/30 5/5 - 4s - loss: 0.8625 - acc: 0.6933 - val_loss: 1.1741 - val_acc: 0.5000 Epoch 2/30 5/5 - 3s - loss: 0.7539 - acc: 0.7467 - val_loss: 1.2036 - val_acc: 0.5333 Epoch 3/30 5/5 - 3s - loss: 0.7829 - acc: 0.7400 - val_loss: 1.2483 - val_acc: 0.5667 Epoch 4/30 5/5 - 3s - loss: 0.6823 - acc: 0.7867 - val_loss: 1.3290 - val_acc: 0.4333 Epoch 5/30 5/5 - 3s - loss: 0.6892 - acc: 0.7800 - val_loss: 1.6482 - val_acc: 0.4333 Epoch 6/30 5/5 - 3s - loss: 0.7903 - acc: 0.7467 - val_loss: 1.0440 - val_acc: 0.6333 Epoch 7/30 5/5 - 3s - loss: 0.5731 - acc: 0.8267 - val_loss: 1.5226 - val_acc: 0.5000 Epoch 8/30 5/5 - 3s - loss: 0.5949 - acc: 0.8333 - val_loss: 0.9984 - val_acc: 0.6667 Epoch 9/30 5/5 - 3s - loss: 0.6162 - acc: 0.8069 - val_loss: 1.1490 - val_acc: 0.5667 Epoch 10/30 5/5 - 3s - loss: 0.7509 - acc: 0.7600 - val_loss: 1.3168 - val_acc: 0.5000 Epoch 11/30 5/5 - 4s - loss: 0.6180 - acc: 0.7862 - val_loss: 1.1918 - val_acc: 0.7000 Epoch 12/30 5/5 - 3s - loss: 0.4936 - acc: 0.8467 - val_loss: 1.0488 - val_acc: 0.6333 Epoch 13/30 5/5 - 3s - loss: 0.4290 - acc: 0.8400 - val_loss: 0.9400 - val_acc: 0.6667 Epoch 14/30 5/5 - 3s - loss: 0.4205 - acc: 0.8533 - val_loss: 1.0716 - val_acc: 0.7000 Epoch 15/30 5/5 - 4s - loss: 0.5750 - acc: 0.8067 - val_loss: 1.2055 - val_acc: 0.6000 Epoch 16/30 5/5 - 4s - loss: 0.4080 - acc: 0.8533 - val_loss: 1.5014 - val_acc: 0.6667 Epoch 17/30 5/5 - 3s - loss: 0.3686 - acc: 0.8467 - val_loss: 1.0441 - val_acc: 0.5667 Epoch 18/30 5/5 - 3s - loss: 0.5474 - acc: 0.8067 - val_loss: 0.9662 - val_acc: 0.7333 Epoch 19/30 5/5 - 3s - loss: 0.5646 - acc: 0.8138 - val_loss: 0.9151 - val_acc: 0.7000 Epoch 20/30 5/5 - 4s - loss: 0.3579 - acc: 0.8800 - val_loss: 1.4184 - val_acc: 0.5667 Epoch 21/30 5/5 - 3s - loss: 0.3714 - acc: 0.8800 - val_loss: 2.0762 - val_acc: 0.6333 Epoch 22/30 5/5 - 3s - loss: 0.3654 - acc: 0.8933 - val_loss: 1.8273 - val_acc: 0.5667 Epoch 23/30 5/5 - 3s - loss: 0.3845 - acc: 0.8933 - val_loss: 1.0199 - val_acc: 0.7333 Epoch 24/30 5/5 - 3s - loss: 0.3356 - acc: 0.9000 - val_loss: 0.5168 - val_acc: 0.8333 Epoch 25/30 5/5 - 3s - loss: 0.3612 - acc: 0.8667 - val_loss: 1.7924 - val_acc: 0.5667 Epoch 26/30 5/5 - 3s - loss: 0.3075 - acc: 0.8867 - val_loss: 1.0720 - val_acc: 0.6667 Epoch 27/30 5/5 - 3s - loss: 0.2820 - acc: 0.9400 - val_loss: 2.2798 - val_acc: 0.5667 Epoch 28/30 5/5 - 3s - loss: 0.3606 - acc: 0.8621 - val_loss: 1.2423 - val_acc: 0.8000 Epoch 29/30 5/5 - 3s - loss: 0.2630 - acc: 0.9000 - val_loss: 1.4235 - val_acc: 0.6333 Epoch 30/30 5/5 - 3s - loss: 0.3790 - acc: 0.9000 - val_loss: 0.6173 - val_acc: 0.8000
La función anterior entrena la red neuronal utilizando el conjunto de entrenamientoEl entrenamiento es un proceso sistemático diseñado para mejorar habilidades, conocimientos o capacidades físicas. Se aplica en diversas áreas, como el deporte, la educación y el desarrollo profesional. Un programa de entrenamiento efectivo incluye la planificación de objetivos, la práctica regular y la evaluación del progreso. La adaptación a las necesidades individuales y la motivación son factores clave para lograr resultados exitosos y sostenibles en cualquier disciplina.... y evalúa su rendimiento en el conjunto de prueba. Las funciones devuelven dos métricas para cada época ‘acc’ y ‘val_acc’ que son la precisión de las predicciones obtenidas en el conjunto de entrenamiento y la precisión alcanzada en el conjunto de prueba, respectivamente.
Conclusión:
Por tanto, vemos que se ha cumplido con la precisión suficiente. Sin embargo, cualquiera puede ejecutar este modelo aumentando el número de épocas o cualquier otro parámetro.
Espero les haya gustado mi artículo. Comparta con sus amigos, colegas.
Los medios que se muestran en este artículo no son propiedad de DataPeaker y se utilizan a discreción del autor.






