Este artículo fue publicado como parte del Blogatón de ciencia de datos.
Introducción
Regresión lineal:
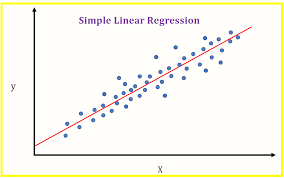
Figura"Figura" es un término que se utiliza en diversos contextos, desde el arte hasta la anatomía. En el ámbito artístico, se refiere a la representación de formas humanas o animales en esculturas y pinturas. En la anatomía, designa la forma y estructura del cuerpo. Además, en matemáticas, "figura" se relaciona con las formas geométricas. Su versatilidad hace que sea un concepto fundamental en múltiples disciplinas.... 1.0: Visualización del modelo de regresión lineal básica
El modelo lineal (regresión lineal) fue probablemente el primer modelo que aprendió y creó, utilizando el modelo para predecir los valores continuos del objetivo. Seguro que debe haber estado feliz de haber completado un modelo. Probablemente también le enseñaron las teorías detrás de su funcionalidad: la minimización de riesgos empíricos, la pérdida media al cuadrado, el descenso del gradienteGradiente es un término utilizado en diversos campos, como la matemática y la informática, para describir una variación continua de valores. En matemáticas, se refiere a la tasa de cambio de una función, mientras que en diseño gráfico, se aplica a la transición de colores. Este concepto es esencial para entender fenómenos como la optimización en algoritmos y la representación visual de datos, permitiendo una mejor interpretación y análisis en..., la tasa de aprendizaje, entre otras.
Bueno, esto es genial y de repente me llamaron para explicarle un modelo que creé al gerente, todos esos términos eran como jergas para él, y cuando pidió la visualización del modelo (como en la figura 1.0) ese es el modelo ajustar el hiperplano (la línea roja) y los puntos de datos (los puntos azules). Me congelé hasta los dedos de los pies sin saber cómo crear eso en código Python.
Bueno, de eso se trata la primera parte de este artículo sobre la creación de la visualización de modelo lineal básico en su cuaderno de Jupyter en Python.
Comencemos a usar estos datos aleatorios:
| X | y |
| 1 | 2 |
| 2 | 3 |
| 3 | 11 |
| 4 | 13 |
| 5 | 28 |
| 6 | 32 |
| 7 | 50 |
| 8 | 59 |
| 9 | 85 |
Método 1: Formulación manual
Importando nuestra biblioteca y creando el marco de datos:

ahora, en esta etapa, hay dos formas de realizar esta visualización:
1.) Usar el conocimiento matemático
2.) El uso del atributo Linear_regression para scikit aprende Linear_model.
- Comencemos con Math😥😥.
simplemente siga adelante, no es tan difícil, primero definimos la ecuación para una relación lineal entre y (variables dependientes / objetivo) y X (variable independiente / características) como:
y = mX + c
donde y = objetivo
X = características
a = pendiente
b = constante de intersección con el eje y
Para crear la ecuación del modelo tenemos que obtener el valor de myc, podemos obtener esto de Y y X con las siguientes ecuaciones:
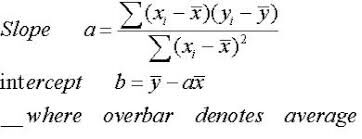
La pendiente, a se interpreta como los producto entre la suma de la diferencia entre cada valor x individual y su media y TLa suma de la diferencia entre cada punto y individual y su media luego dividido por la suma del cuadrado de cada x individual y su media.
La intersección es simplemente la media de y menos el producto de la pendiente y la media de x
Eso es mucho para asimilar. Probablemente lo lea una y otra vez hasta que lo entienda, intente leer con la imagen
👆👆 ese fue el único desafío; si lo has entendido felicidades sigamos adelante.
Ahora escribir esto en código Python es ‘eazy-pizzy’ usando la biblioteca numpy, compruébalo👇👇.
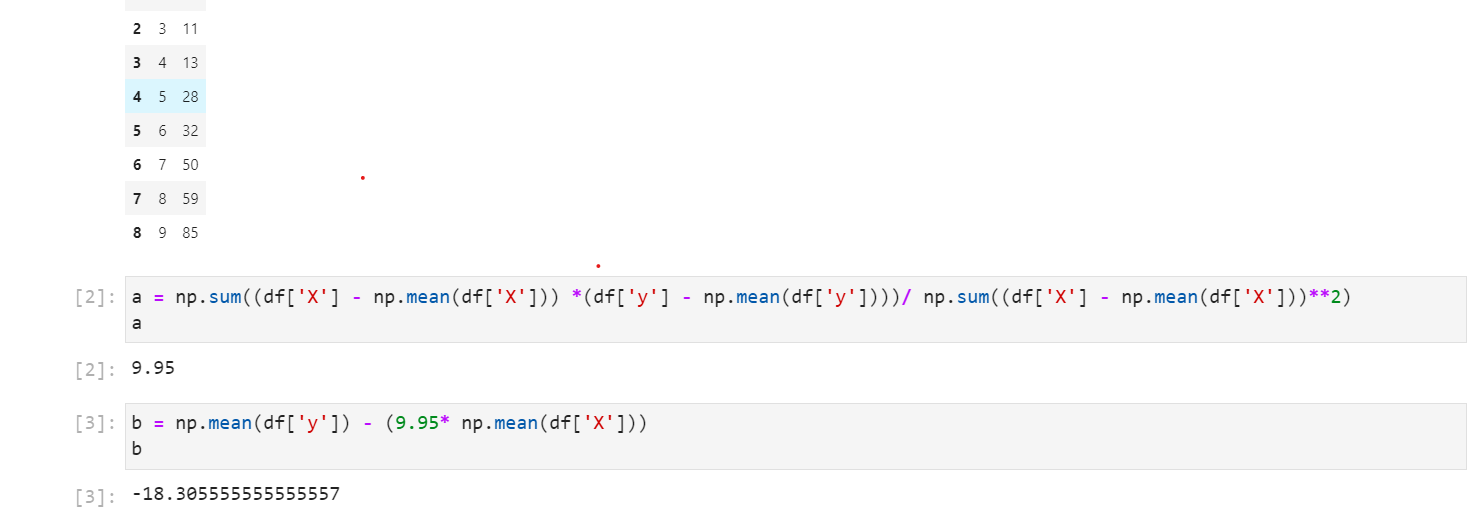
ahora tenemos nuestro a y b, simplemente lo insertamos en la ecuación —-> y = 9,95 -1218,56x
Para volar tu mente ahora, ¿sabías que esta es la ecuación del modelo? y acabamos de crear un modelo sin usar scikit learn. lo confirmaremos ahora usando el segundo método que es el paquete scikit learn Linear Regression
Método 2: usar la regresión lineal de scikit-learn
Wseremos importando la regresión lineal de scikit learn, ajusta los datos en el modelo y luego confirma la pendiente y la intersección. Los pasos están en la imagen de abajo.
para que pueda ver que casi no hay diferencia, ahora visualicemos esto como en la figura 1.

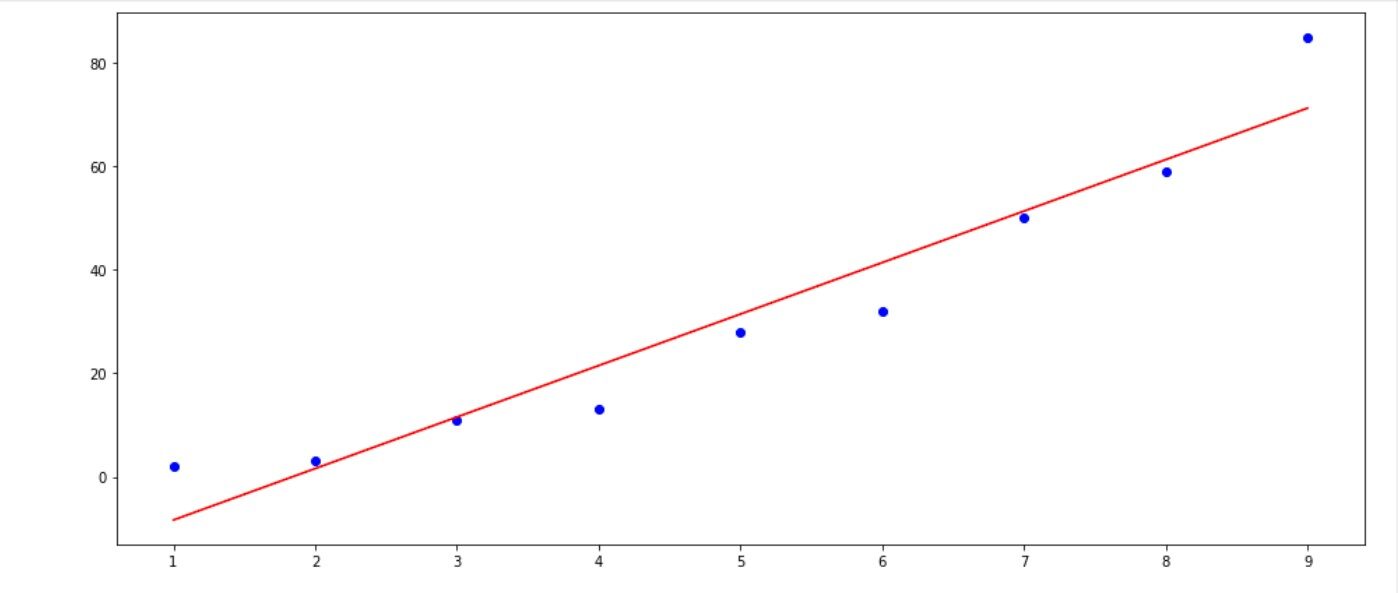
La línea roja es nuestra línea de mejor ajuste que se utilizará para la predicción y el punto azul son nuestros datos iniciales. Con esto, tenía algo que informar al gerente. Particularmente hice esto para cada función con el objetivo de agregar más información.
Ahora hemos logrado nuestro objetivo de crear un modelo y mostrar su gráfico trazado.
Esta técnica puede llevar mucho tiempo cuando se trata de datos con tamaños más grandes y solo debe usarse al visualizar su línea de mejor ajuste con una característica en particular para fines de análisis. No es realmente necesario durante el modelado a menos que se solicite. Los errores y el cálculo pueden consumir su tiempo y recursos de cálculo, especialmente si está trabajando con datos 3D y superiores. Pero la información obtenida vale la pena.
Espero que te haya gustado el artículo, si es así de genial, también puedes decirme cómo mejorar de alguna manera. Todavía tengo mucho que compartir, especialmente sobre regresiones (lineal, logística y polinomial).
Gracias por leer.






