Detección y tratamiento de valores atípicos | Cómo manejar valores atípicos

Introducción:

Uno de los pasos más importantes como parte del preprocesamiento de datos es detectar y tratar los valores atípicos, ya que pueden afectar negativamente el análisis estadístico y el proceso de entrenamientoEl entrenamiento es un proceso sistemático diseñado para mejorar habilidades, conocimientos o capacidades físicas. Se aplica en diversas áreas, como el deporte, la educación y el desarrollo profesional. Un programa de entrenamiento efectivo incluye la planificación de objetivos, la práctica regular y la evaluación del progreso. La adaptación a las necesidades individuales y la motivación son factores clave para lograr resultados exitosos y sostenibles en cualquier disciplina.... de un algoritmo de aprendizaje automático, lo que resulta en una menor precisión.

1. ¿Qué son los valores atípicos? 🤔

Todos hemos oído hablar del modismo ‘extraño, que significa algo inusual en comparación con los demás en un grupo.

De manera similar, un valor atípico es una observación en un conjunto de datos dado que se encuentra lejos del resto de las observaciones. Eso significa que un valor atípico es mucho más grande o más pequeño que los valores restantes del conjunto.

2. ¿Por qué ocurren?

Un valor atípico puede ocurrir debido a la variabilidad en los datos, o debido a un error experimental / error humano.

Pueden indicar un error experimental o una gran asimetría en los datos (distribución de cola pesada).

3. ¿Qué afectan?

En estadística, tenemos tres medidas de tendencia central: Media, MedianaLa mediana es una medida estadística que representa el valor central de un conjunto de datos ordenados. Para calcularla, se organizan los datos de menor a mayor y se identifica el número que se encuentra en el medio. Si hay un número par de observaciones, se promedia los dos valores centrales. Este indicador es especialmente útil en distribuciones asimétricas, ya que no se ve afectado por valores extremos.... y Moda. Nos ayudan a describir los datos.

La media es la medidaLa "medida" es un concepto fundamental en diversas disciplinas, que se refiere al proceso de cuantificar características o magnitudes de objetos, fenómenos o situaciones. En matemáticas, se utiliza para determinar longitudes, áreas y volúmenes, mientras que en ciencias sociales puede referirse a la evaluación de variables cualitativas y cuantitativas. La precisión en la medición es crucial para obtener resultados confiables y válidos en cualquier investigación o aplicación práctica.... precisa para describir los datos cuando no tenemos valores atípicos presentes.

La mediana se usa si hay un valor atípico en el conjunto de datos.

El modo se utiliza si hay un valor atípico Y aproximadamente la mitad o más de los datos son iguales.

La «media» es la única medida de tendencia central que se ve afectada por los valores atípicos, lo que a su vez afecta la desviación estándar.

Ejemplo:

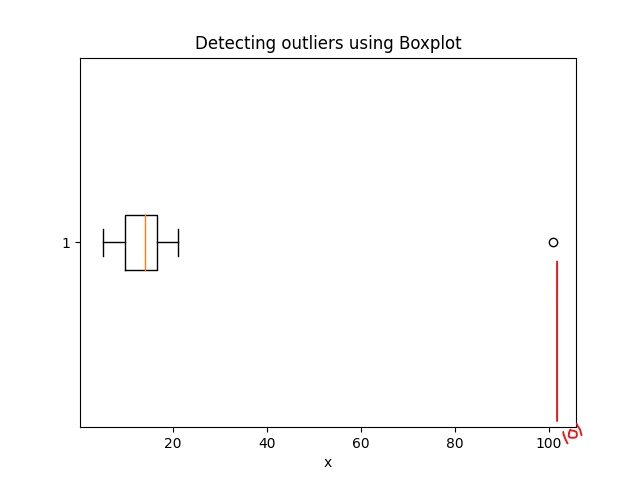
Considere un pequeño conjunto de datos, muestra = [15, 101, 18, 7, 13, 16, 11, 21, 5, 15, 10, 9]. Al mirarlo, se puede decir rápidamente que ‘101’ es un valor atípico que es mucho más grande que los otros valores.

De los cálculos anteriores, podemos decir claramente que la Media se ve más afectada que la Mediana.

4. Detección de valores atípicos

Si nuestro conjunto de datos es pequeño, podemos detectar el valor atípico con solo mirar el conjunto de datos. Pero, ¿qué pasa si tenemos un gran conjunto de datos, cómo identificamos los valores atípicos? Necesitamos utilizar técnicas de visualización y matemáticas.

A continuación se muestran algunas de las técnicas para detectar valores atípicos.

• Diagramas de cajaLos diagramas de caja, también conocidos como diagramas de caja y bigotes, son herramientas estadísticas que representan la distribución de un conjunto de datos. Estos diagramas muestran la mediana, los cuartiles y los valores atípicos, lo que permite visualizar la variabilidad y la simetría de los datos. Son útiles en la comparación entre diferentes grupos y en el análisis exploratorio, facilitando la identificación de tendencias y patrones en los datos....
• Puntuación Z
• Intervalo entre cuantiles (IQR)

4.1 Detección de valores atípicos mediante Boxplot:

El código de Python para el diagrama de caja es:

import matplotlib.pyplot as plt
plt.boxplot(sample, vert=False)
plt.title("Detecting outliers using Boxplot")
plt.xlabel('Sample')

4.2 Detección de valores atípicos utilizando las puntuaciones Z

Criterios: cualquier punto de datos cuya puntuación Z caiga fuera de la 3ª desviación estándar es un valor atípico.

Pasos:

• recorrer todos los puntos de datos y calcular el puntaje Z usando la fórmula (Xi-mean) / std.
• defina un valor de umbral de 3 y marque los puntos de datos cuyo valor absoluto de Z-score sea mayor que el umbral como valores atípicos.

import numpy as np
outliers = []
def detect_outliers_zscore(data):
    thres = 3
    mean = np.mean(data)
    std = np.std(data)
    # print(mean, std)
    for i in data:
        z_score = (i-mean)/std
        if (np.abs(z_score) > thres):
            outliers.append(i)
    return outliers# Driver code
sample_outliers = detect_outliers_zscore(sample)
print("Outliers from Z-scores method: ", sample_outliers)

Los resultados del código anterior: Valores atípicos del método de puntuaciones Z: [101]

4.3 Detección de valores atípicos utilizando el rango entre cuantiles (IQR)

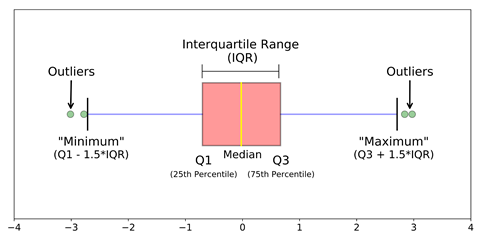
Criterios: los puntos de datos que se encuentran 1,5 veces el IQR por encima de Q3 y por debajo de Q1 son valores atípicos.

pasos:

• Ordene el conjunto de datos en orden ascendente
• calcular el primer y tercer cuartiles (Q1, Q3)
• calcular IQR = Q3-Q1
• calcular límite inferior = (Q1–1.5 * IQR), límite superior = (Q3 + 1.5 * IQR)
• recorrer los valores del conjunto de datos y verificar aquellos que caen por debajo del límite inferior y por encima del límite superior y marcarlos como valores atípicos

Código Python:

outliers = []
def detect_outliers_iqr(data):
    data = sorted(data)
    q1 = np.percentile(data, 25)
    q3 = np.percentile(data, 75)
    # print(q1, q3)
    IQR = q3-q1
    lwr_bound = q1-(1.5*IQR)
    upr_bound = q3+(1.5*IQR)
    # print(lwr_bound, upr_bound)
    for i in data: 
        if (i<lwr_bound or i>upr_bound):
            outliers.append(i)
    return outliers# Driver code
sample_outliers = detect_outliers_iqr(sample)
print("Outliers from IQR method: ", sample_outliers)

Los resultados del código anterior: Valores atípicos del método IQR: [101]

5. Manejo de valores atípicos

Hasta ahora aprendimos sobre la detección de valores atípicos. La pregunta principal es ¿QUÉ hacemos con los valores atípicos?

A continuación se muestran algunos de los métodos para tratar los valores atípicos.

• Recortar / eliminar el valor atípico
• Revestimientos y pavimentos a base de cuantiles
• Imputación media / mediana

5.1 Recorte / Eliminación de valores atípicos

En esta técnica, eliminamos los valores atípicos del conjunto de datos. Aunque no es una buena práctica a seguir.

Código de Python para eliminar el valor atípico y copiar el resto de los elementos a otra matriz.

# Trimming
for i in sample_outliers:
    a = np.delete(sample, np.where(sample==i))
print(a)
# print(len(sample), len(a))

El valor atípico ‘101’ se elimina y el resto de los puntos de datos se copian en otra matriz ‘a’.

5.2 Revestimientos y pavimentos basados ​​en cuantiles

En esta técnica, el valor atípico se limita a un cierto valor por encima del valor del percentil 90 o se reduce a un factor por debajo del valor del percentil 10.

Código Python:

# Computing 10th, 90th percentiles and replacing the outliers
tenth_percentile = np.percentile(sample, 10)
ninetieth_percentile = np.percentile(sample, 90)
# print(tenth_percentile, ninetieth_percentile)b = np.where(sample<tenth_percentile, tenth_percentile, sample)
b = np.where(b>ninetieth_percentile, ninetieth_percentile, b)
# print("Sample:", sample)
print("New array:",b)

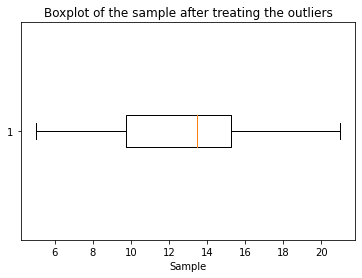
Los resultados del código anterior: Nueva matriz: [15, 20.7, 18, 7.2, 13, 16, 11, 20.7, 7.2, 15, 10, 9]

Los puntos de datos que son menores que el percentil 10 se reemplazan con el valor del percentil 10 y los puntos de datos que son mayores que el percentil 90 se reemplazan con el valor del percentil 90.

5.3 imputación media / mediana

Como el valor medio está muy influenciado por los valores atípicos, se recomienda reemplazar los valores atípicos con el valor mediano.

Código Python:

median = np.median(sample)# Replace with median
for i in sample_outliers:
    c = np.where(sample==i, 14, sample)
print("Sample: ", sample)
print("New array: ",c)
# print(x.dtype)

Visualización de los datos después de tratar el valor atípico

plt.boxplot(c, vert=False)
plt.title("Boxplot of the sample after treating the outliers")
plt.xlabel("Sample")

Resumen:

En este blog, aprendimos sobre una fase importante del preprocesamiento de datos que es el tratamiento de valores atípicos. Ahora conocemos diferentes métodos para detectar y tratar valores atípicos.

Referencias:

Puntaje Z para la detección de valores atípicos

IQR para detección de valores atípicos

Método Python numpy.where ()

Repositorio de GitHub para consultar el cuaderno de Jupyter

Espero que este blog ayude a comprender el concepto de valores atípicos. Por favor, vote a favor si le gusta. Feliz aprendizaje !! 😊

Los medios que se muestran en este artículo no son propiedad de DataPeaker y se utilizan a discreción del autor.

Relacionado