Este artículo fue publicado como parte del Blogatón de ciencia de datos.
Introducción
En la publicación anterior, definimos las distribuciones de probabilidad y discutimos brevemente las diferentes distribuciones de probabilidad discreta. En esta publicación, continuaremos aprendiendo sobre distribuciones de probabilidad a través de Distribuciones de probabilidad continuas.
Definición
Si recuerda nuestra discusión anterior, las variables aleatorias continuas pueden tomar un número infinito de valores en un intervalo dado. Por ejemplo, en el intervalo [2, 3] hay valores infinitos entre 2 y 3. Las distribuciones continuas se definen mediante las funciones de densidad de probabilidad (PDF) en lugar de las funciones de masa de probabilidad. La probabilidad de que una variableEn estadística y matemáticas, una "variable" es un símbolo que representa un valor que puede cambiar o variar. Existen diferentes tipos de variables, como las cualitativas, que describen características no numéricas, y las cuantitativas, que representan cantidades numéricas. Las variables son fundamentales en experimentos y estudios, ya que permiten analizar relaciones y patrones entre diferentes elementos, facilitando la comprensión de fenómenos complejos.... aleatoria continua sea igual a un valor exacto siempre es igual a cero. Las probabilidades continuas se definen sobre un intervalo. Por ejemplo, P (X = 3) = 0 pero P (2.99 <X <3.01) se puede calcular integrando la PDF sobre el intervalo [2.99, 3.01]
Lista de distribuciones de probabilidad continua
A continuación, analizamos las distribuciones de probabilidad continua más utilizadas:
1. Distribución uniforme continua
La distribución uniforme tiene formas tanto continuas como discretas. Aquí, discutimos el continuo. Esta distribución traza las variables aleatorias cuyos valores tienen la misma probabilidad de ocurrir. El ejemplo más común es lanzar un dado justo. Aquí, los 6 resultados tienen la misma probabilidad de ocurrir. Por tanto, la probabilidad es constante.
Considere el ejemplo donde a = 10 y b = 20, la distribución se ve así:
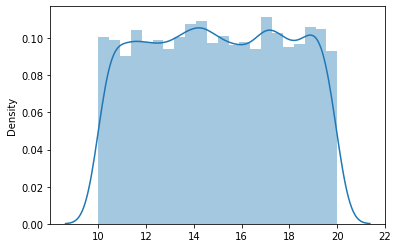
El PDF está dado por,
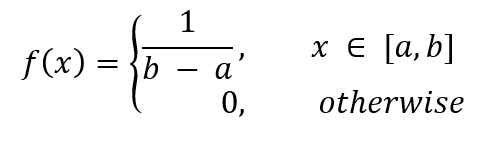
donde a es el valor mínimo y b es el valor máximo.
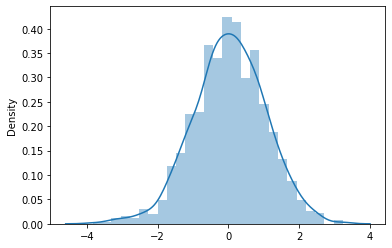
2. Distribución normal
Esta es la distribución más discutida y que se encuentra con mayor frecuencia en el mundo real. Muchas distribuciones continuas a menudo alcanzan una distribución normal dada una muestra lo suficientemente grande. Esto tiene dos parámetrosLos "parámetros" son variables o criterios que se utilizan para definir, medir o evaluar un fenómeno o sistema. En diversos campos como la estadística, la informática y la investigación científica, los parámetros son fundamentales para establecer normas y estándares que guían el análisis y la interpretación de datos. Su adecuada selección y manejo son cruciales para obtener resultados precisos y relevantes en cualquier estudio o proyecto...., a saber, la desviación estándar y la media.
Esta distribución tiene muchas propiedades interesantes. La media tiene la probabilidad más alta y todos los demás valores se distribuyen por igual a ambos lados de la media de forma simétrica. La distribución normal estándar es un caso especial donde la media es 0 y la desviación estándar de 1.
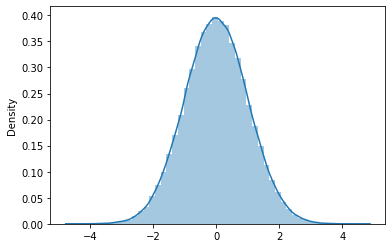
También sigue la fórmula empírica de que el 68% de los valores están a 1 desviación estándar de distancia, el 95% por ciento de ellos están a 2 desviaciones estándar de distancia y el 99,7% están a 3 desviaciones estándar de la media. Esta propiedad es muy útil al diseñar pruebas de hipótesis (https://www.statisticshowto.com/probability-and-statistics/hypothesis-testing/).
El PDF está dado por,
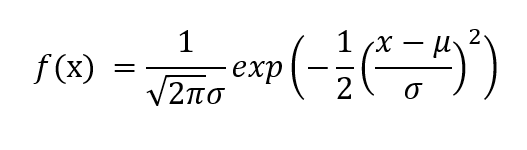
donde μ es la media de la variable aleatoria X y σ es la desviación estándar.
3. Distribución logarítmica normal
Esta distribución se utiliza para graficar las variables aleatorias cuyos valores de logaritmo siguen una distribución normal. Considere las variables aleatorias X e Y. Y = ln (X) es la variable que se representa en esta distribución, donde ln denota el logaritmo natural de los valores de X.
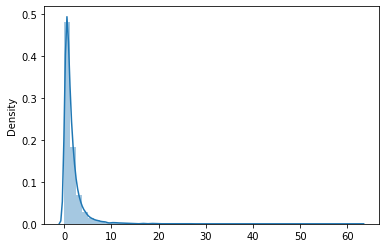
El PDF está dado por,
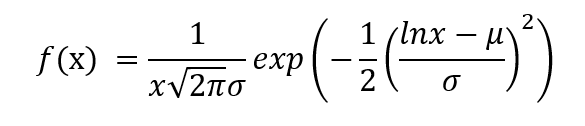
donde μ es la media de Y y σ es la desviación estándar de Y.
4. Distribución T de Student
La distribución t de Student es similar a la distribución normal. La diferencia es que las colas de la distribución son más gruesas. Se utiliza cuando el tamaño de la muestra es pequeño y no se conoce la varianza de la población. Esta distribución se define por los grados de libertad (p) que se calculan como el tamaño de la muestra menos 1 (n – 1).
A medida que aumenta el tamaño de la muestra, los grados de libertad aumentan, la distribución t se acerca a la distribución normal y las colas se vuelven más estrechas y la curva se acerca a la media. Esta distribución se utiliza para probar estimaciones de la media de la población cuando el tamaño de la muestra es inferior a 30 y se desconoce la varianza de la población. La varianza / desviación estándar de la muestra se utiliza para calcular el valor t.
El PDF está dado por,
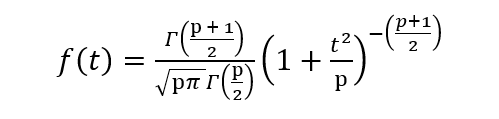
donde p son los grados de libertad y Γ es la función gamma. Consulte este enlace para obtener una breve descripción de la función gamma.
El estadístico t utilizado en la prueba de hipótesis se calcula de la siguiente manera,
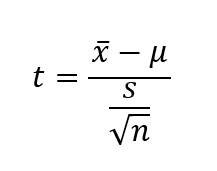
donde x̄ es la media de la muestra, μ la media de la población ys es la varianza de la muestra.
5. Distribución de chi-cuadrado
Esta distribución es igual a la suma de cuadrados de p variables aleatorias normales. p es el número de grados de libertad. Al igual que la distribución t, a medida que aumentan los grados de libertad, la distribución se aproxima gradualmente a la distribución normal. A continuación se muestra una distribución de chi-cuadrado con tres grados de libertad.
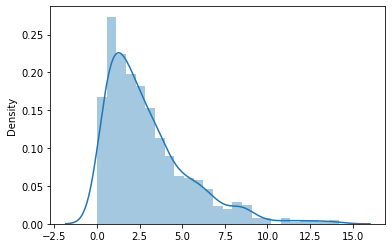
El PDF está dado por,
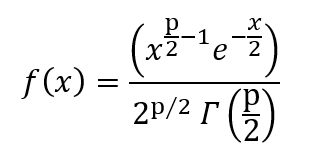
donde p son los grados de libertad y Γ es la función gamma.
El valor de chi-cuadrado se calcula de la siguiente manera:
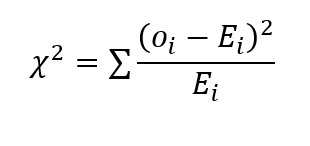
donde o es el valor observado y E representa el valor esperado. Esto se utiliza en la prueba de hipótesis para extraer inferencias sobre la varianza poblacional de las distribuciones normales.
6. Distribución exponencial
Recuerde la distribución de probabilidad discreta que hemos discutido en la publicación de Probabilidad discreta. En la distribución de Poisson, tomamos el ejemplo de las llamadas recibidas por el centro de atención al cliente. En ese ejemplo, consideramos el número promedio de llamadas por hora. Ahora, en esta distribución, se explica el tiempo entre llamadas sucesivas.
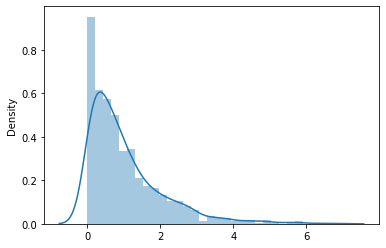
La distribución exponencial puede verse como una inversa de la distribución de Poisson. Los eventos en consideración son independientes entre sí.
El PDF está dado por,
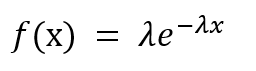
donde λ es el parámetro de tasa. λ = 1 / (tiempo medio entre eventos).
Para concluir, hemos discutido muy brevemente diferentes distribuciones de probabilidad continua en esta publicación. No dude en agregar comentarios o sugerencias a continuación.
Sobre mí
Soy Priyanka Madiraju, una ex ingeniera de software que trabaja en la transición a la ciencia de datos. Soy estudiante de maestría en Data Science. No dude en conectarse conmigo en https://www.linkedin.com/in/priyanka-madiraju
Los medios que se muestran en este artículo no son propiedad de DataPeaker y se utilizan a discreción del autor.






