Introducción
“No se puede probar una hipótesis; solo puedes mejorarlo o refutarlo «. – Christopher Monckton
Todos los días nos encontramos probando nuevas ideas, encontrando la ruta más rápida a la oficina, la forma más rápida de terminar nuestro trabajo o simplemente encontrando una mejor manera de hacer algo que amamos. La pregunta crítica, entonces, es si nuestra idea es significativamente mejor que lo que probamos anteriormente.
Estas ideas que se nos ocurren de manera tan regular, eso es esencialmente lo que es una hipótesis. Y probar estas ideas para descubrir cuál funciona y cuál es mejor dejar atrás, se llama prueba de hipótesis.
La prueba de hipótesis es una de las cosas más fascinantes que hacemos como científicos de datos. Ninguna idea está fuera de los límites en esta etapa de nuestro proyecto. Personalmente, he visto muchas ideas surgidas de la prueba de hipótesis, ¡ideas que la mayoría de nosotros nos habríamos perdido si no fuera por esta etapa!
Una de las formas más populares de probar una hipótesis es un concepto llamado prueba t. Existen diferentes tipos de pruebas t, como veremos pronto, y cada una tiene su propia aplicación única. Si es un aspirante a científico de datos, debe saber qué es una prueba t y cuándo puede aprovecharla.
Entonces, en este artículo, aprenderemos sobre los diversos matices de una prueba t y luego veremos los tres tipos diferentes de pruebas t. La guinda del pastel? Implementaremos cada tipo de prueba t en R para visualizar cómo funcionan en escenarios prácticos. ¡Vámonos!
Nota: debe leer el artículo a continuación si necesita repasar los conceptos de prueba de hipótesis:
Tabla de contenido
- ¿Cuándo debemos realizar una prueba t?
- Supuestos para realizar una prueba t
- Tipos de pruebas t (con ejemplos resueltos en R)
- Prueba t para una muestra
- Prueba t independiente para dos muestras
- Prueba t de muestras pareadas
¿Cuándo debemos realizar una prueba t?
Primero entendamos dónde se puede usar una prueba t antes de sumergirnos en sus diferentes tipos y sus implementaciones. Creo firmemente que la mejor manera de aprender un concepto es visualizarlo a través de un ejemplo. Así que tomemos un ejemplo simple para ver dónde resulta útil una prueba t.
Considere una empresa de telecomunicaciones que tiene dos centros de servicio en la ciudad. La empresa quiere saber si el tiempo medio necesario para atender a un cliente es el mismo en ambas tiendas.
Fuente: Shopworks
La empresa mide el tiempo medio que tardan 50 clientes aleatorios en cada tienda. La Tienda A tarda 22 minutos, mientras que la Tienda B tiene un promedio de 25 minutos. ¿Podemos decir que la Tienda A es más eficiente que la Tienda B en términos de servicio al cliente?
Parece así, ¿no? Sin embargo, solo hemos analizado a 50 clientes aleatorios de las muchas personas que visitan las tiendas. Es posible que simplemente mirar el tiempo de muestra promedio no sea representativo de todos los clientes que visitan ambas tiendas.
Aquí es donde entra en juego la prueba t. Nos ayuda a comprender si la diferencia entre dos medias muestrales es realmente real o simplemente se debe al azar.
Supuestos para realizar una prueba t
Hay ciertas suposiciones que debemos tener en cuenta antes de realizar una prueba t:
- Los datos deben seguir una escala continua u ordinal (los puntajes de las pruebas de CI de los estudiantes, por ejemplo)
- Las observaciones en los datos deben seleccionarse al azar
- Los datos deben parecerse a una curva en forma de campana cuando los trazamos, es decir, deben estar distribuidos normalmente. Puede consultar este artículo para comprender mejor la distribución normal
- Se debe tomar un tamaño de muestra grande para que los datos se acerquen a una distribución normal (unaunque la prueba t es esencial para muestras pequeñas ya que sus distribuciones no son normales)
- Las variaciones entre los grupos deben ser iguales (fo prueba t independiente de dos muestras)
Entonces, ¿cuáles son los diferentes tipos de pruebas t? ¿Cuándo debemos realizar cada tipo? Responderemos estas preguntas en la siguiente sección y veremos cómo podemos realizar cada tipo de prueba t en R.
Tipos de pruebas t (con ejemplos resueltos en R)
Hay tres tipos de pruebas t que podemos realizar en función de los datos disponibles:
- Prueba t de una muestra
- Prueba t independiente de dos muestras
- Prueba t de muestras pareadas
En esta sección, veremos cada uno de estos tipos en detalle. También proporcioné el código R para cada tipo de prueba t para que pueda seguirlos mientras los implementamos. ¡Es una excelente manera de aprender y ver cuán útiles son estas pruebas t!
Prueba t para una muestra
En una prueba t de una muestra, comparamos el promedio (o media) de un grupo con el promedio (o media) establecido. Este promedio establecido puede ser cualquier valor teórico (o puede ser la media de la población).
Considere el siguiente ejemplo: un investigador desea determinar si el tiempo promedio para comer una hamburguesa (de tamaño estándar) difiere de un valor establecido. Digamos que este valor es de 10 minutos. ¿Cómo cree que el investigador puede determinar esto?
Él / ella puede seguir ampliamente los siguientes pasos:
- Seleccionar un grupo de personas
- Registre el tiempo de ingesta individual de una hamburguesa de tamaño estándar.
- Calcule el tiempo medio de comida del grupo.
- Finalmente, compare ese valor promedio con el valor establecido de 10
En pocas palabras, así es como podemos realizar una prueba t de una muestra. Aquí está la fórmula para calcular esto:
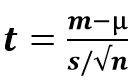
dónde,
- t = estadístico t
- m = media del grupo
- µ = valor teórico o media poblacional
- s = desviación estándar del grupo
- n = tamaño del grupo o tamaño de la muestra
Nota: Como se mencionó anteriormente en los supuestos de que se debe tomar un tamaño de muestra grande para que los datos se acerquen a una distribución normal. (Aunque la prueba t es esencial para muestras pequeñas ya que sus distribuciones no son normales).
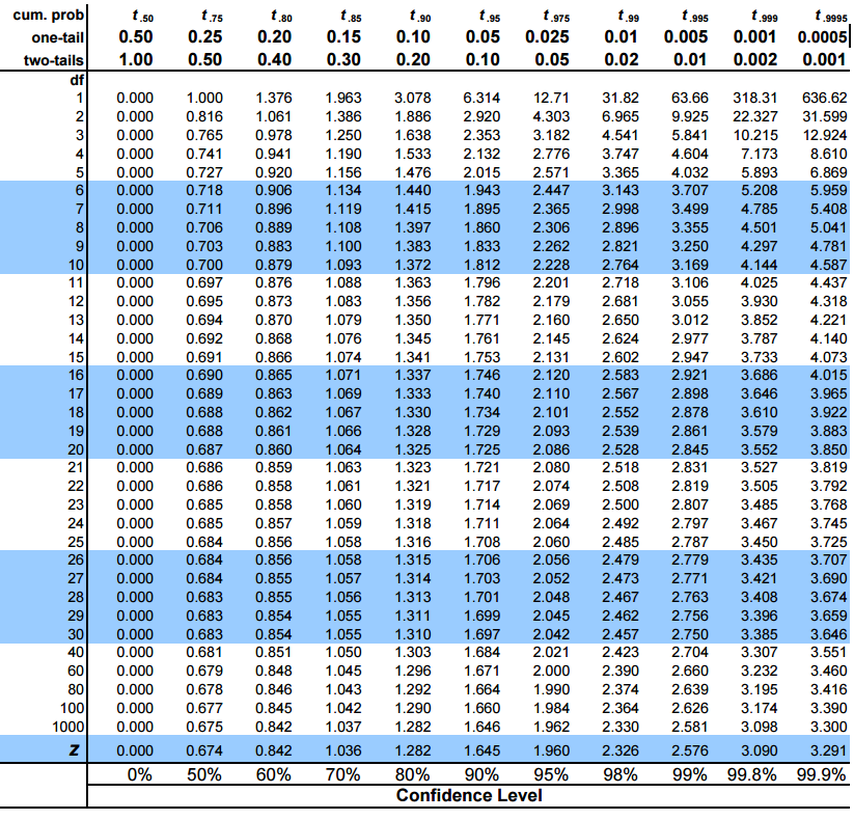
Una vez que hemos calculado el valor del estadístico t, la siguiente tarea es compararlo con el valor crítico de la prueba t. Podemos encontrar esto en la siguiente tabla de prueba t contra el grado de libertad (n-1) y el nivel de significancia:
Este método nos ayuda a comprobar si la diferencia entre las medias es estadísticamente significativa o no. Consolidemos aún más nuestra comprensión de una prueba t de una muestra realizándola en R.
Implementación de la prueba t de una muestra en R
Una empresa de fabricación de móviles ha tomado una muestra de móviles del mismo modelo a partir de los datos del mes anterior. Quieren comprobar si el tamaño medio de pantalla de la muestra difiere de la longitud deseada de 10 cm. Puedes descargar los datos aquí.
Paso 1: Primero, importe los datos.
Paso 2: Validarlo para que sea correcto en R:
Producción:
#Count of Rows and columns [1] 1000 1 > #View top 10 rows of the dataset Screen_size.in.cm. 1 10.006692 2 10.081624 3 10.072873 4 9.954496 5 9.994093 6 9.952208 7 9.947936 8 9.988184 9 9.993365 10 10.016660
Paso 3: ¿Recuerda las suposiciones que discutimos anteriormente? Necesitamos revisarlos:
Obtenemos la siguiente gráfica QQ:
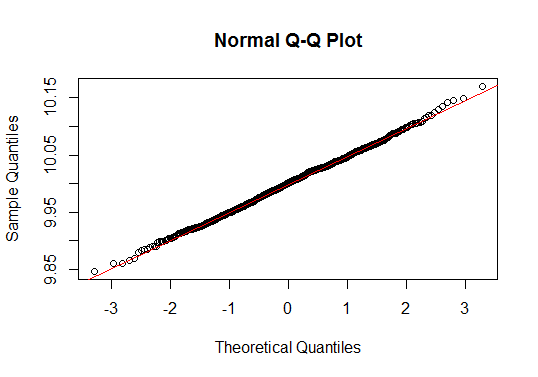
Casi todos los valores se encuentran en la línea roja. Podemos decir con seguridad que los datos siguen una distribución normal.
Paso 4: Realice una prueba t de una muestra:
Producción:
One Sample t-test data: data$Screen_size.in.cm. t = -0.39548, df = 999, p-value = 0.6926 alternative hypothesis: true mean is not equal to 10 95 percent confidence interval: 9.996361 10.002418 sample estimates: mean of x 9.99939
El estadístico t resulta ser -0,39548. Tenga en cuenta que aquí podemos tratar los valores negativos como su contraparte positiva. Ahora, consulte la tabla mencionada anteriormente para conocer el valor t crítico. El grado de libertad aquí es 999 y el intervalo de confianza es del 95%.
El valor t-crítico es 1,962. Dado que el estadístico t es menor que el valor t crítico, no rechazamos la hipótesis nulaLa hipótesis nula es un concepto fundamental en la estadística que establece una afirmación inicial sobre un parámetro poblacional. Su propósito es ser probada y, en caso de ser refutada, permite aceptar la hipótesis alternativa. Este enfoque es esencial en la investigación científica, ya que proporciona un marco para evaluar la evidencia empírica y tomar decisiones basadas en datos. Su formulación y análisis son cruciales en estudios estadísticos.... y podemos concluir que el tamaño de pantalla promedio de la muestra no difiere de 10 cm.
También podemos verificar esto a partir del valor p, que es mayor que 0.05. Por lo tanto, no rechazamos la hipótesis nula en un intervalo de confianza del 95%.
Prueba t independiente de dos muestras
La prueba t de dos muestras se utiliza para comparar las medias de dos muestras diferentes.
Digamos que queremos comparar la altura promedio de los empleados masculinos con la altura promedio de las mujeres. Por supuesto, el número de hombres y mujeres debería ser igual para esta comparación. Aquí es donde se usa una prueba t de dos muestras.
Aquí está la fórmula para calcular el estadístico t para una prueba t de dos muestras:
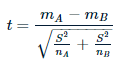
dónde,
- metroA y MB son los medios de dos muestras diferentes
- norteA y NB son los tamaños de muestra
- S2 es un estimadorEl "Estimador" es una herramienta estadística utilizada para inferir características de una población a partir de una muestra. Se basa en métodos matemáticos para proporcionar estimaciones precisas y confiables. Existen diferentes tipos de estimadores, como los insesgados y los consistentes, que se eligen según el contexto y el objetivo del estudio. Su correcto uso es fundamental en investigaciones científicas, encuestas y análisis de datos.... de la varianza común de dos muestras, como:
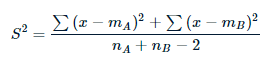
Aquí, el grado de libertad es nA + nB – 2.
Seguiremos la misma lógica que vimos en una prueba t de una muestra para verificar si el promedio de un grupo es significativamente diferente de otro grupo. Así es, compararemos el estadístico t calculado con el valor t crítico.
Tomemos un ejemplo de una prueba t independiente de dos muestras y resuélvala en R.
Implementación de la prueba t de dos muestras en R
Para esta sección, trabajaremos con datos sobre dos muestras de los distintos modelos de un teléfono móvil. Queremos comprobar si el tamaño de pantalla medio de la muestra 1 difiere del tamaño de pantalla medio de la muestra 2. Puede descargar los datos aquí.
Paso 1: Nuevamente, primero importe los datos.
Paso 2: Validarlo para que sea correcto en R:
Paso 3: Necesitamos verificar las suposiciones como hicimos anteriormente. Dejaré ese ejercicio en tus manos ahora.
Además, en este caso, comprobaremos la homogeneidad de la varianza:
Producción:
#Homogeneity of variance > var(data$screensize_sample1) [1] 0.00238283 > var(data$screensize_sample2) [1] 0.002353585
Genial, las variaciones son iguales. Podemos seguir adelante.
Paso 4: Realice la prueba t de dos muestras independientes:
Nota: Vuelva a escribir el código anterior con “var.equal = F” si obtiene variaciones desiguales o desconocidas. Este será un caso de Prueba t de Welch que se utiliza para comparar las medias de dos muestras con varianzas desiguales.
Producción:
Two Sample t-test data: data$screensize_sample1 and data$screensize_sample2 t = 1.3072, df = 1998, p-value = 0.1913 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -0.001423145 0.007113085 sample estimates: mean of x mean of y 10.000976 9.998131
¿Qué puede inferir del resultado anterior? Podemos confirmar que el estadístico t es nuevamente menor que el valor crítico t, por lo que no rechazamos la hipótesis nula. Por lo tanto, podemos concluir que no hay diferencia entre el tamaño de pantalla medio de ambas muestras.
Podemos verificar esto nuevamente usando el valor p. Resulta ser mayor que 0.05, por lo tanto, no rechazamos la hipótesis nula en un intervalo de confianza del 95%. No hay diferencia entre la media de las dos muestras.
Prueba t de muestras pareadas
La prueba t de muestras pareadas es bastante intrigante. Aquí, medimos un grupo en dos momentos diferentes. Comparamos medias separadas para un grupo en dos momentos diferentes o bajo dos condiciones diferentes. ¿Confundido? Dejame explicar.
Cierto gerente se dio cuenta de que el nivel de productividad de sus empleados tenía una tendencia significativamente descendente. Este gerente decidió realizar un programa de capacitación para todos sus empleados con el objetivo de incrementar sus niveles de productividad.
¿Cómo medirá el gerente si aumentaron los niveles de productividad? Es simple: simplemente compare el nivel de productividad de los empleados antes y después del programa de capacitación.
Aquí, comparamos la misma muestra (los empleados) en dos momentos diferentes (antes y después de la capacitación). Este es un ejemplo de una prueba t pareada. La fórmula para calcular el estadístico t para una prueba t pareada es:
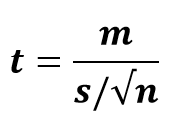
dónde,
- t = estadístico t
- m = media del grupo
- µ = valor teórico o media poblacional
- s = desviación estándar del grupo
- n = tamaño del grupo o tamaño de la muestra
Podemos tomar el grado de libertad en esta prueba como n – 1 ya que solo está involucrado un grupo. Ahora, resolvamos un ejemplo en R.
Implementación de la prueba t pareada en R
El gerente de una empresa de fabricación de neumáticos quiere comparar el material de caucho de dos lotes de neumáticos. Una forma de hacer esto: verifique la diferencia entre los kilómetros promedio recorridos por un lote de neumáticos hasta que se gasten.
Puede descargar los datos desde aquí. ¡Hagámoslo!
Paso 1: Primero, importe los datos.
Paso 2: Validarlo para que sea correcto en R:
Paso 3: Ahora verificamos las suposiciones tal como lo hicimos en una prueba t de una muestra. De nuevo, te dejo esto.
Paso 4: Realice la prueba t pareada:
Producción:
Paired t-test data: data$tyre_1 and data$tyre_2 t = -5.2662, df = 24, p-value = 2.121e-05 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -2201.6929 -961.8515 sample estimates: mean of the differences -1581.772
¡Debe ser un experto en descifrar esta salida a esta altura! El valor p es menor que 0.05. Podemos rechazar la hipótesis nula con un intervalo de confianza del 95% y concluir que existe una diferencia significativa entre las medias de los neumáticos antes y después del reemplazo del material de caucho.
La media negativa de la diferencia muestra que los kilómetros medios recorridos por el neumático 2 son más que los kilómetros medios recorridos por el neumático 1.
Notas finales
En este artículo, aprendimos sobre el concepto de prueba t, sus supuestos y también los tres tipos diferentes de pruebas t con sus implementaciones en R. La prueba t tiene tanto significado estadístico como aplicaciones prácticas en el mundo real. .
Si es nuevo en las estadísticas, desea cubrir sus conceptos básicos y también desea comenzar en la ciencia de datos, le recomiendo tomar el Curso de introducción a la ciencia de datos. Le brinda una descripción general completa de las estadísticas descriptivas e inferenciales antes de sumergirse en las técnicas de ciencia de datos.
¿Le resultó útil este artículo? ¿Puedes pensar en otras aplicaciones de la prueba t? ¡Házmelo saber en la sección de comentarios a continuación y podemos tener más ideas!
