Este artículo fue publicado como parte del Blogatón de ciencia de datos.
Visión general
ble, ¿verdad? Agrupamos los puntos de datos en 3 grupos en función de su similitud o cercanía.
Tabla de contenido
1.Introducción a las medias K
2.K medias ++ algoritmo
3.¿Cómo elegir el valor K en K medias?
4.Consideraciones prácticas en K medias
5.Tendencia de clúster
1. Introducción
Simplemente entendamos la agrupación de K-medias con ejemplos de la vida diaria. sabemos que en estos días a todo el mundo le encanta ver series web o películas en Amazon Prime, Netflix. ¿Alguna vez has observado algo cada vez que abres Netflix? es decir, agrupar películas en función de su género, es decir, crimen, suspenso, etc., espero que lo hayas observado o ya lo sepas. por lo que la agrupación por géneros de Netflix es un ejemplo fácil de entender la agrupación. entendamos más sobre k significa algoritmo de agrupación en clústeres.
Definición: Agrupa los puntos de datos en función de su similitud o cercanía entre sí, en términos simples, el algoritmo necesita encontrar los puntos de datos cuyos valores son similares entre sí y, por lo tanto, estos puntos pertenecerían al mismo grupo.
Entonces, ¿cómo encuentra el algoritmo los valores entre dos puntos para agruparlos? El algoritmo encuentra los valores usando el método de ‘Medida de distancia’. aquí la medida de la distancia es ‘Distancia euclidiana’
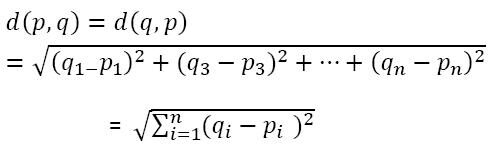
Las observaciones más cercanas o similares entre sí tendrían una distancia euclidiana baja y luego se agruparían.
una fórmula más que necesita saber para entender los medios de K es ‘Centroide’. El algoritmo de k-medias usa el concepto de centroide para crear ‘k grupos’.
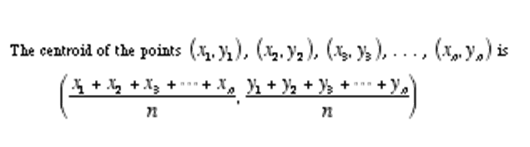
Así que ahora está listo para comprender los pasos del algoritmo de agrupación en clústeres de k-medias.
Pasos en K-medias:
paso 1: elija el valor k para ex: k = 2
paso 2: inicializar centroides aleatoriamente
Paso 3: calcule la distancia euclidiana desde los centroides a cada punto de datos y forme grupos que estén cerca de los centroides
paso 4: encuentre el centroide de cada grupo y actualice los centroides
paso: 5 repita el paso 3
Cada vez que se hacen grupos, los centroides se actualizan, el centroide actualizado es el centro de todos los puntos que caen en el grupo. Este proceso continúa hasta que el centroide ya no cambia, es decir, la solución converge.
Puede jugar con el algoritmo K-means usando el siguiente enlace, pruébelo.
https://stanford.edu/class/engr108/visualizations/kmeans/kmeans.html
Entonces, ¿qué sigue? ¿Cómo eliges los centroides iniciales al azar?
Aquí viene el concepto del algoritmo k-Means ++.
2. Algoritmo K-Means ++:
No te voy a estresar más por esto, así que no te preocupes. Es muy fácil de entender. Entonces, ¿qué es k-means ++ ??? Digamos que queremos elegir dos centroides inicialmente (k = 2), puede elegir un centroide al azar o puede elegir uno de los puntos de datos al azar. simple ¿verdad? Nuestra siguiente tarea es elegir otro centroide, ¿cómo lo eliges? ¿alguna idea?
Elegimos el siguiente centroide de los puntos de datos que está a una gran distancia del centroide existente o el que está a una gran distancia de un grupo existente que tiene una alta probabilidad de captar.
3.Cómo elegir el valor K en K-medias:
1.Método del codo
pasos:
Paso 1: calcular el algoritmo de agrupación en clústeres para diferentes valores de k.
por ejemplo k =[1,2,3,4,5,6,7,8,9,10]
paso 2: para cada k, calcule la suma de cuadrados dentro del conglomerado (WCSS).
Paso 3: trazar la curva de WCSS según el número de conglomerados.
Paso 4: La ubicación de la curva en la parcela generalmente se considera un indicador del número aproximado de conglomerados.
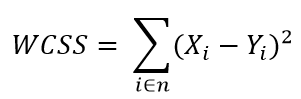
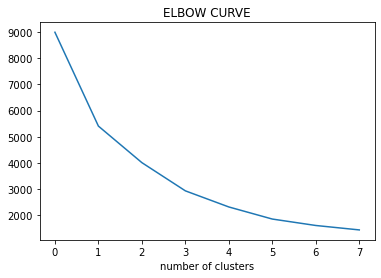
Consideraciones prácticas en K-medias:
- Un número de clústeres elegido por adelantado (K).
- Estandarización de datos (escalado).
- Datos categóricos (se puede resolver con el modo K).
- Impacto de los centroides y valores atípicos iniciales.
5. Tendencia de clúster:
Antes de aplicar un algoritmo de agrupación en clústeres a los datos dados, es importante verificar si los datos dados tienen algunos clústeres significativos o no. El proceso para evaluar los datos para verificar si los datos son factibles para la agrupación o no se conoce como ‘Tendencia de agrupación’, por lo que no debemos aplicar ciegamente el método de agrupación y debemos verificar la tendencia de agrupación. ¿Cómo?
Usamos la ‘Estadística de Hopkins’ para saber si realizar la agrupación en clústeres o no para un conjunto de datos dado. Examina si los puntos de datos difieren significativamente de los datos distribuidos uniformemente en un espacio multidimensional.
Con esto concluye nuestro artículo sobre el algoritmo de agrupamiento de k-means. En mi próximo artículo, hablaré sobre la implementación de Python del algoritmo de agrupación en clústeres K-means.
¡Gracias!
Los medios que se muestran en este artículo no son propiedad de DataPeaker y se utilizan a discreción del autor.






