Este artículo fue publicado como parte del Blogatón de ciencia de datos

¿Es usted un aspirante a científico de datos que está fascinado por cómo funcionan las cosas en el mundo de la ciencia de datos y el aprendizaje automático? Bueno, enhorabuena por elegir la carrera profesional adecuada que mejor se adapte a sus necesidades en este momento. Sin embargo, ¿sabía que necesita dominar las matemáticas para el aprendizaje automático y la ciencia de datos? Sí, has escuchado bien.
No importa qué tipo de relación de amor-odio tuviste con las matemáticas en la escuela. Los conceptos básicos que se utilizan en matemáticas y estadística son en realidad muy útiles para tomar decisiones estratégicas al diseñar modelos de aprendizaje automático. Entonces, si ha decidido elegir esta carrera en el campo de la ciencia de datos, debe comenzar a amar los conceptos de las matemáticas e implementarlos en su futuro, ya que es uno de los requisitos previos para el aprendizaje automático.
¿Cuál es la correlación entre el aprendizaje automático y las matemáticas?

El aprendizaje automático tiene que ver con las matemáticas, lo que a su vez ayuda a crear un algoritmo que puede aprender de los datos para hacer una predicción precisa. La predicción podría ser tan simple como clasificar perros o gatos a partir de un conjunto determinado de imágenes o qué tipo de productos recomendar a un cliente en función de compras anteriores. Por lo tanto, es muy importante comprender adecuadamente los conceptos matemáticos detrás de cualquier algoritmo central de aprendizaje automático. De esta forma, le ayuda a elegir todos los algoritmos adecuados para su proyecto en ciencia de datos y aprendizaje automático.
El aprendizaje automático se basa principalmente en prerrequisitos matemáticos, por lo que siempre que pueda comprender por qué se utilizan las matemáticas, lo encontrará más interesante. Con esto, comprenderá por qué elegimos un algoritmo de aprendizaje automático sobre el otro y cómo afecta el rendimiento del modelo de aprendizaje automático.
Puntos que se tratarán en esta publicación de blog
-
¿Qué conceptos matemáticos están involucrados en el aprendizaje automático?
-
¿Por qué necesita matemáticas en proyectos de aprendizaje automático?
-
¿Cuál es la forma correcta de aprenderlo?
En la publicación del blog de hoy, discutiremos exactamente todos los conceptos matemáticos que necesita aprender para dominar los conceptos de ciencia de datos y aprendizaje automático. También aprenderemos por qué usamos las matemáticas en el aprendizaje automático con algunos ejemplos.
Comencemos analizando las muchas formas de matemáticas utilizadas en la ciencia de datos y el aprendizaje automático para que pueda comprender mejor lo que realmente necesita saber sobre las matemáticas para la profesión de la ciencia de datos.
Qué conceptos matemáticos se implementan en ciencia de datos y aprendizaje automático
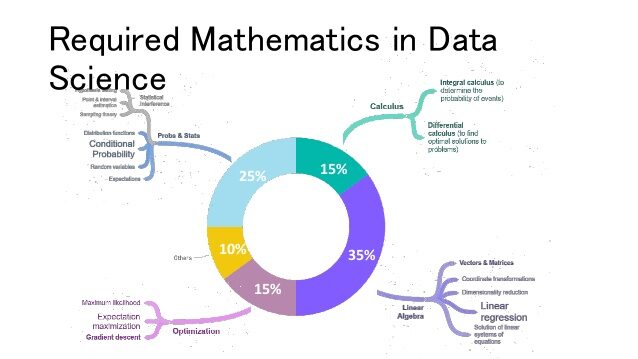
El aprendizaje automático se basa en cuatro conceptos críticos y es estadística, álgebra lineal, probabilidad y cálculo. Si bien los conceptos estadísticos son la parte central de cada modelo, el cálculo nos ayuda a aprender y optimizar un modelo. El álgebra lineal es excepcionalmente útil cuando se trata de un gran conjunto de datos y la probabilidad ayuda a predecir el sustento de los eventos que ocurrirán. Estos son los conceptos matemáticos que encontrará en su carrera de ciencia de datos y aprendizaje automático con bastante frecuencia.
Conceptos matemáticos importantes para el aprendizaje automático y la ciencia de datos:
-
Álgebra lineal
-
Cálculo
-
Teoría de probabilidad
-
Matemáticas discretas
-
Estadísticas
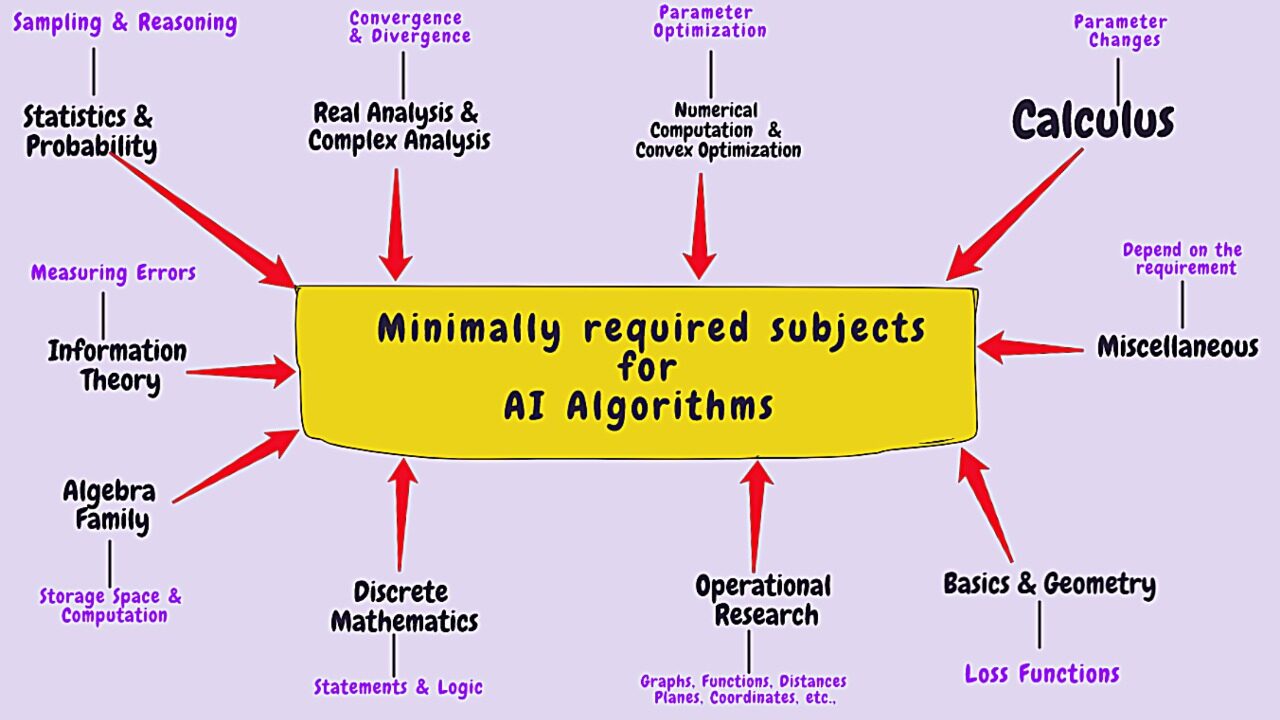
Concepto de álgebra lineal en el aprendizaje automático:
Comprender cómo construir ecuaciones lineales es un componente fundamental en el desarrollo de algoritmos centrales de aprendizaje automático. Estos se utilizarán para evaluar y observar la recopilación de datos. El álgebra lineal se aplica en algoritmos de aprendizaje automático en funciones de pérdida, regularizaciónLa regularización es un proceso administrativo que busca formalizar la situación de personas o entidades que operan fuera del marco legal. Este procedimiento es fundamental para garantizar derechos y deberes, así como para fomentar la inclusión social y económica. En muchos países, la regularización se aplica en contextos migratorios, laborales y fiscales, permitiendo a quienes se encuentran en situaciones irregulares acceder a beneficios y protegerse de posibles sanciones...., matrices de covarianza, descomposición de valores singulares (SVD), operaciones matriciales y clasificación de máquinas vectoriales de soporte. También se aplica en algoritmos de aprendizaje automático como la regresión lineal. Estos son los conceptos necesarios para comprender los métodos de optimización utilizados para el aprendizaje automático.
Para realizar un análisis de componentes principales que se utiliza para reducir la dimensionalidad de los datos, utilizamos álgebra lineal. El álgebra lineal también se usa mucho en redes neuronales para el procesamiento y representación de redes. No hace falta decir que debe estar interesado en el álgebra lineal, ya que se usa ampliamente en el campo de la ciencia de datos.
Sin embargo, no se deje intimidar por esto, ya que comprender los conceptos será importante, pero no es necesario ser un experto en álgebra lineal para resolver la mayoría de los problemas. Solo un conocimiento sólido de los conceptos será lo suficientemente bueno. Matemáticas para el aprendizaje automático de Marc Peter deisenroth es un libro excelente que le ayudará a comenzar este viaje si tiene dificultades con las matemáticas al principio.
Cálculo en el aprendizaje automático:
Muchos estudiantes a los que no les gustó aprender cálculo que se les enseñó en la escuela se encontrarán con un duro golpe, ya que es una parte integral del aprendizaje automático. Afortunadamente, es posible que no necesite dominar el cálculo, solo es importante aprender y comprender los principios del cálculo. Además, debe comprender las aplicaciones prácticas del aprendizaje automático a través del cálculo durante la construcción del modelo.
Entonces, si comprende cómo la derivada de la función devuelve su tasa de cambio en el cálculo, podrá comprender el concepto de descenso de gradienteGradiente es un término utilizado en diversos campos, como la matemática y la informática, para describir una variación continua de valores. En matemáticas, se refiere a la tasa de cambio de una función, mientras que en diseño gráfico, se aplica a la transición de colores. Este concepto es esencial para entender fenómenos como la optimización en algoritmos y la representación visual de datos, permitiendo una mejor interpretación y análisis en.... En el descenso de gradiente, necesitamos encontrar los mínimos locales para una función y así sucesivamente. Si tiene puntos de silla o múltiples mínimos, un descenso de gradiente puede encontrar un mínimo local y no un mínimo global, a menos que comience desde múltiples puntos. Algunos de los temas necesarios para dominar la parte de cálculo en ciencia de datos son Cálculo diferencial e integral, Derivadas parciales, Funciones de valores vectoriales, Gradientes direccionales.
El cálculo multivariado se utiliza en el entrenamientoEl entrenamiento es un proceso sistemático diseñado para mejorar habilidades, conocimientos o capacidades físicas. Se aplica en diversas áreas, como el deporte, la educación y el desarrollo profesional. Un programa de entrenamiento efectivo incluye la planificación de objetivos, la práctica regular y la evaluación del progreso. La adaptación a las necesidades individuales y la motivación son factores clave para lograr resultados exitosos y sostenibles en cualquier disciplina.... de algoritmos, así como en el descenso de gradientes. Derivadas, divergencia, curvatura y aproximaciones cuadráticas son conceptos importantes que puede aprender e implementar.
Las matemáticas del aprendizaje automático pueden parecerle intimidantes en este momento, sin embargo, podrá comprender los conceptos de cálculo que se requieren para construir un modelo de aprendizaje automático exitoso en unos pocos días de aprendizaje constructivo.
Uso de estadísticas descriptivas
La estadística descriptiva es un concepto fundamental que todo científico de datos aspirante debe aprender a comprender el aprendizaje automático cuando trabaja con clasificaciones como regresión logística, distribuciones, análisis de discriminación y pruebas de hipótesis.
Si estaba luchando con la estadística en la escuela, entonces debe poner su 200 por ciento para aprender la parte matemática de la estadística, ya que es muy esencial para que se convierta en un científico de datos exitoso. Para decirlo en palabras más simples, la estadística es la parte principal de las matemáticas para el aprendizaje automático. Algunas de las estadísticas fundamentales necesarias para ML son Combinatoria, Axiomas, Teorema de Bayes, Varianza y Expectativa, Variables Aleatorias, Distribuciones Condicionales y Conjuntas.
Matemáticas discretas en el aprendizaje automático
Las matemáticas discretas se ocupan de los números no continuos, la mayoría de las veces enteros. Muchas aplicaciones requieren el uso de números discretos. Al programar una flota de taxis, por ejemplo, no puede enviar 0,34 taxis; debe enviar los completos. No se puede tener medio cartero o hacer que visite 1 y medio lugares para entregar las cartas.
Muchas de las estructuras de la inteligencia artificial son discretas. Una red neuronalLas redes neuronales son modelos computacionales inspirados en el funcionamiento del cerebro humano. Utilizan estructuras conocidas como neuronas artificiales para procesar y aprender de los datos. Estas redes son fundamentales en el campo de la inteligencia artificial, permitiendo avances significativos en tareas como el reconocimiento de imágenes, el procesamiento del lenguaje natural y la predicción de series temporales, entre otros. Su capacidad para aprender patrones complejos las hace herramientas poderosas..., por ejemplo, tiene un número entero de nodos e interconexiones. No puede tener 0,65 nodos o una novena parte de un enlace. Como resultado, las matemáticas utilizadas para construir una red neuronal deben incluir un elemento discreto, el número entero representa el número de nodos e interconexiones.
Puede salirse con la suya con los fundamentos de las matemáticas discretas para el aprendizaje automático, a menos que desee trabajar con dominios relacionales, modelos gráficos, problemas combinatorios, predicción estructurada, etc. Para dominar estos conceptos, debe consultar libros sobre matemáticas discretas. Afortunadamente para los graduados en ciencias de la computación, estos conceptos están cubiertos adecuadamente en su universidad. Sin embargo, es posible que otros tengan que esforzarse más para comprender este tema. Por lo tanto, las matemáticas discretas son un componente muy importante de AI & ML.
Teoría de la probabilidad en el aprendizaje automático
Para trabajar correctamente en un proyecto de modelado predictivo de aprendizaje automático, sería razonable concluir que la probabilidad es esencial.
El aprendizaje automático es el proceso de creación de modelos de predicción a partir de datos ambiguos. Trabajar con información defectuosa o incompleta es lo que conlleva la incertidumbre.
La incertidumbre es crucial para el aprendizaje automático, sin embargo, es uno de los componentes que crea más dificultades para los recién llegados, particularmente aquellos que provienen de una experiencia en programación.
En el aprendizaje automático, hay tres fuentes principales de incertidumbre: datos ruidosos, cobertura limitada del área del problema y, por supuesto, modelos imperfectos. Sin embargo, con la ayuda de las herramientas de probabilidad adecuadas, podemos estimar la solución al problema.
La probabilidad es esencial para las pruebas de hipótesis y distribuciones como la distribución gaussiana y la función de densidad de probabilidad.
Veamos ahora las aplicaciones una vez que hayamos analizado los tipos en matemáticas y ciencia de datos.
¿Por qué debería preocuparse por las matemáticas? ¿Por qué necesita matemáticas en proyectos de aprendizaje automático?
Existen numerosas razones por las que las matemáticas para el aprendizaje automático son importantes, y compartiré algunos de los consejos importantes a continuación:
-
La elección del mejor algoritmo requiere tener en cuenta la precisión, el tiempo de entrenamiento, la complejidad del modelo, el número de parámetrosLos "parámetros" son variables o criterios que se utilizan para definir, medir o evaluar un fenómeno o sistema. En diversos campos como la estadística, la informática y la investigación científica, los parámetros son fundamentales para establecer normas y estándares que guían el análisis y la interpretación de datos. Su adecuada selección y manejo son cruciales para obtener resultados precisos y relevantes en cualquier estudio o proyecto.... y el número de funciones.
-
Elección de valores de parámetros y métodos de validación.
-
Comprender la compensación de sesgo-varianza le permite identificar problemas de sobreajuste y desajuste que normalmente ocurren al ejecutar el programa.
-
Determinación del intervalo de confianza y la incertidumbre correctos.
¿Cuál es la forma correcta de aprender matemáticas para la ciencia de datos y el aprendizaje automático?

Aunque hay muchos recursos valiosos disponibles en Internet que explican conceptos como el cálculo de vectores de descomposición de matrices, la matriz de geometría analíticaLa analítica se refiere al proceso de recopilar, medir y analizar datos para obtener información valiosa que facilite la toma de decisiones. En diversos campos, como los negocios, la salud y el deporte, la analítica permite identificar patrones y tendencias, optimizar procesos y mejorar resultados. El uso de herramientas avanzadas y técnicas estadísticas es fundamental para transformar datos en conocimiento aplicable y estratégico.... de álgebra lineal, las matemáticas detrás del análisis de componentes principales y las máquinas de vectores de soporte. No todos los recursos son una solución integral para su comprensión. Por lo tanto, he recopilado una lista de libros, sitios web y canales de YouTube que pueden ayudarlo a mejorar su concepto teórico en el campo de la inteligencia artificial.
-
Matemáticas para el aprendizaje automático de Marc Peter Deisenroth es el libro que puede ayudarlo a comenzar su viaje matemático. Se han explicado claramente las aplicaciones prácticas de los algoritmos y las matemáticas detrás de ellos. Todos los conceptos de las matemáticas se han explicado correctamente. Puede consultar el pdf en línea aquí -https: //mml-book.github.io/book/mml-book.pdf
-
Cálculo multivariado por Imperial College London – El Imperial College London básicamente ha creado una serie de YouTube que cubre los conceptos importantes del cálculo multivariante y su aplicación en varios algoritmos ml. Aunque todo el curso está en colaboración con Coursera, Imperial College London lo ha puesto a disposición de forma gratuita para todos los estudiantes curiosos.
-
Cursos de Khan Academy sobre Álgebra lineal, Probabilidad y estadística, Cálculo multivariable, y Mejoramiento– Un recurso muy completo y gratuito disponible para que todos los estudiantes amplíen sus conocimientos en conceptos complejos como la matriz de geometría analítica de álgebra lineal.
-
Todas las estadísticas: un curso conciso de inferencia estadística por Larry Wasserman es supuestamente otro recurso exhaustivo que contiene una explicación detallada de conceptos importantes como
-
De Udacity Introducción a la estadística– es otro recurso gratuito a través del cual puede obtener un nivel inicial de comprensión en el campo de las estadísticas que se necesita para la ciencia de datos.
Conclusión
Le llevará entre 3 y 4 meses aprender los conceptos matemáticos y ponerlos en práctica. Consulte los recursos mencionados anteriormente y no olvide seguir aprendiéndolo junto con los algoritmos de aprendizaje automático para que pueda comprender cuál es el algoritmo correcto que debe elegir para su modelo.
Los medios que se muestran en este artículo no son propiedad de Analytics Vidhya y se utilizan a discreción del autor.






