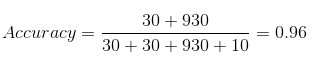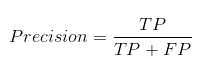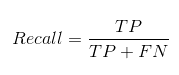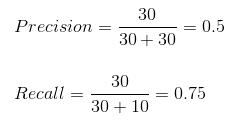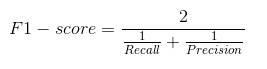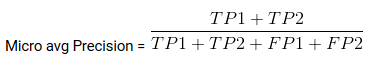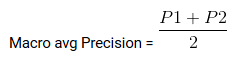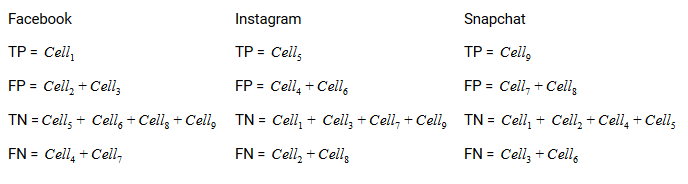Matriz de confusión para el aprendizaje automático

Matriz de confusión: ¡no tan confusa!

¿Ha estado en una situación en la que esperaba que su modelo de aprendizaje automático funcionara verdaderamente bien, pero arrojó una precisión deficiente? Has hecho todo el trabajo duro, entonces, ¿dónde salió mal el modelo de clasificación? ¿Cómo puedes corregir esto?

Hay muchas alternativas para medir el rendimiento de su modelo de clasificación, pero ninguna ha resistido la prueba del tiempo como la matriz de confusión. Nos ayuda a examinar cómo funcionó nuestro modelo, dónde salió mal y nos ofrece una guía para corregir nuestro camino.

En este post, exploraremos cómo una matriz de confusión brinda una visión holística del desempeño de su modelo. Y a diferencia de su nombre, se dará cuenta de que una matriz de confusión es un concepto bastante simple pero poderoso. ¡Por lo tanto desentrañemos el misterio en torno a la matriz de confusión!

¿Aprendiendo las cuerdas en el campo del aprendizaje automático? Estos cursos te ayudarán a seguir tu camino:

Esto es lo que cubriremos:

• ¿Qué es una matriz de confusión?
  • Verdadero Positivo
  • Verdadero negativo
  • Falso positivo: error tipo 1
  • Falso negativo – Error de tipo 2
• ¿Por qué necesita una matriz de confusión?
• Precisión vs recuperación
• Puntuación F1
• Matriz de confusión en Scikit-learn
• Matriz de confusión para clasificación de clases múltiples

¿Qué es una matriz de confusión?

La pregunta del millón de dólares: ¿qué es, después de todo, una matriz de confusión?

Una matriz de confusión es una matriz N x N que se utiliza para examinar el rendimiento de un modelo de clasificación, donde N es el número de clases objetivo. La matriz compara los valores objetivo reales con los predichos por el modelo de aprendizaje automático. Esto nos da una visión holística de qué tan bien se está desempeñando nuestro modelo de clasificación y qué tipo de errores está cometiendo.

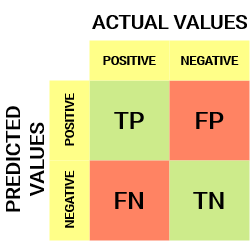
Para un obstáculo de clasificación binaria, tendríamos una matriz de 2 x 2 como se muestra a continuación con 4 valores:

Descifremos la matriz:

• La variableEn estadística y matemáticas, una "variable" es un símbolo que representa un valor que puede cambiar o variar. Existen diferentes tipos de variables, como las cualitativas, que describen características no numéricas, y las cuantitativas, que representan cantidades numéricas. Las variables son fundamentales en experimentos y estudios, ya que permiten analizar relaciones y patrones entre diferentes elementos, facilitando la comprensión de fenómenos complejos.... de destino tiene dos valores: Positivo o Negativo
• los columnas representar el valores actuales de la variable objetivo
• los filas representar el valores predichos de la variable objetivo

Pero espera, ¿qué es TP, FP, FN y TN aquí? Esa es la parte crucial de una matriz de confusión. Entendamos cada término a continuación.

Comprender el verdadero positivo, el verdadero negativo, el falso positivo y el falso negativo en una matriz de confusión

Verdadero positivo (TP)

• El valor predicho coincide con el valor real
• El valor real fue positivo y el modelo predijo un valor positivo.

Verdadero negativo (TN)

• El valor predicho coincide con el valor real
• El valor real fue negativo y el modelo predijo un valor negativo.

Falso positivo (FP): error de tipo 1

• El valor predicho fue predicho falsamente
• El valor real fue negativo pero el modelo predijo un valor positivo
• Además conocido como el Error tipo 1

Falso negativo (FN): error de tipo 2

• El valor predicho fue predicho falsamente
• El valor real fue positivo pero el modelo predijo un valor negativo
• Además conocido como el Error de tipo 2

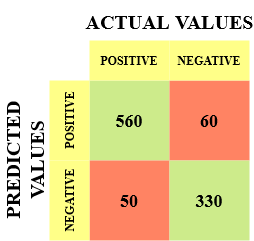
Déjame darte un ejemplo para saber mejor esto. Supongamos que tenemos un conjunto de datos de clasificación con 1000 puntos de datos. Le colocamos un clasificador y obtenemos la próxima matriz de confusión:

Los diferentes valores de la matriz de confusión serían los siguientes:

• Verdadero positivo (TP) = 560; lo que significa que 560 puntos de datos de clase positivos fueron clasificados correctamente por el modelo
• Verdadero negativo (TN) = 330; lo que significa que 330 puntos de datos de clase negativos fueron clasificados correctamente por el modelo
• Falso positivo (FP) = 60; lo que significa que el modelo clasificó incorrectamente 60 puntos de datos de clase negativa como pertenecientes a la clase positiva
• Falso negativo (FN) = 50; lo que significa que el modelo clasificó incorrectamente 50 puntos de datos de clase positiva como pertenecientes a la clase negativa

Este resultó ser un clasificador bastante decente para nuestro conjunto de datos considerando el número relativamente mayor de valores verdaderos positivos y verdaderos negativos.

Recuerde los errores de Tipo 1 y Tipo 2. ¡A los entrevistadores les encanta preguntar la diferencia entre estos dos! Puede prepararse mejor para todo esto desde nuestro Curso de aprendizaje automático en línea

¿Por qué necesitamos una matriz de confusión?

Antes de responder a esta pregunta, pensemos en un obstáculo de clasificación hipotético.

Supongamos que desea predecir cuántas personas están infectadas con un virus contagioso antes de que muestren los síntomas y aislarlas de la población sana (¿aún suena algo? 😷). Los dos valores de nuestra variable objetivo serían: Enfermo y No Enfermo.

Ahora, debe preguntarse: ¿por qué necesitamos una matriz de confusión cuando tenemos nuestro amigo para todo clima: precisión? Bueno, veamos dónde falla la precisión.

Nuestro conjunto de datos es un ejemplo de conjunto de datos desequilibrado. Hay 947 puntos de datos para la clase negativa y 3 puntos de datos para la clase positiva. Así es como calcularemos la precisión: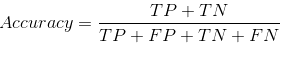

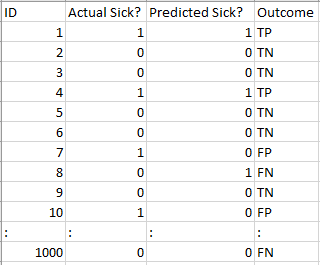
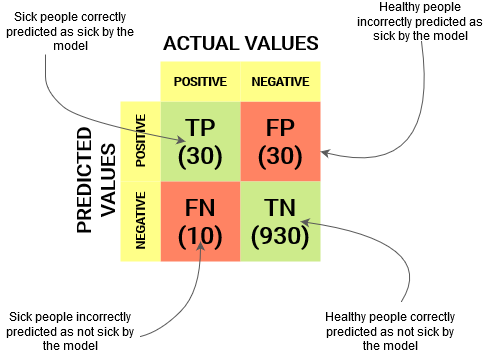
Veamos cómo funcionó nuestro modelo:

Los valores de resultado totales son:

TP = 30, TN = 930, FP = 30, FN = 10

Entonces, la precisión de nuestro modelo resulta ser:

96%! ¡Nada mal!

Pero está dando una idea equivocada sobre el resultado. Piénsalo.

Nuestro modelo dice «Puedo predecir personas enfermas el 96% del tiempo». A pesar de esto, está haciendo lo contrario. ¡Está prediciendo las personas que no se enfermarán con un 96% de precisión mientras los enfermos están propagando el virus!

¿Crees que esta es una métrica correcta para nuestro modelo dada la gravedad del problema? ¿No deberíamos medir cuántos casos positivos podemos predecir correctamente para detener la propagación del virus contagioso? O tal vez, de los casos predichos correctamente, ¿cuántos son casos positivos para verificar la confiabilidad de nuestro modelo?

Aquí es donde nos encontramos con el concepto dual de Precision y Recall.

Precisión frente a recuperación

La precisión nos dice cuántos de los casos predichos correctamente resultaron verdaderamente positivos.

A continuación, se explica cómo calcular la precisión:

Esto determinaría si nuestro modelo es confiable o no.

Recall nos dice cuántos de los casos positivos reales pudimos predecir correctamente con nuestro modelo.

Y así es como podemos calcular Recall:

Podemos calcular fácilmente Precision y Recall para nuestro modelo conectando los valores en las preguntas anteriores:

El 50% de los casos predichos correctamente resultaron ser casos positivos. Mientras que nuestro modelo predijo con éxito el 75% de los positivos. ¡Impresionante!

La precisión es una métrica útil en los casos en que los falsos positivos son una preocupación mayor que los falsos negativos.

La precisión es esencial en los sistemas de recomendación de música o video, sitios web de comercio electrónico, etc. Los resultados incorrectos pueden provocar la pérdida de clientes y ser perjudiciales para la compañía.

La recuperación es una métrica útil en los casos en que el falso negativo triunfa sobre el falso positivo.

El recuerdo es esencial en casos médicos en los que no importa si damos una falsa alarma, ¡pero los casos positivos reales no deben pasar desapercibidos!

En nuestro ejemplo, Recall sería una mejor métrica debido a que no queremos dar de alta accidentalmente a una persona infectada y dejar que se mezcle con la población sana propagando así el virus contagioso. Ahora puede comprender por qué la precisión fue una mala métrica para nuestro modelo.

Pero habrá casos en los que no haya una distinción clara entre si la precisión es más importante o la recuperación. ¿Qué debemos hacer en esos casos? ¡Los combinamos!

Puntuación F1

En la práctica, cuando intentamos incrementar la precisión de nuestro modelo, la recuperación disminuye y viceversa. La puntuación F1 captura ambas tendencias en un solo valor:

La puntuación F1 es una media armónica de precisión y recuperación, por lo que da una idea combinada sobre estas dos métricas. Es máximo cuando Precision es igual a Recall.

Pero hay una trampa aquí. La interpretabilidad de la puntuación F1 es pobre. Esto significa que no sabemos qué está maximizando nuestro clasificador: ¿precisión o recuerdo? Entonces, lo usamos en combinación con otras métricas de evaluación que nos brindan una imagen completa del resultado.

Matriz de confusión usando scikit-learn en Python

Ya conoces la teoría, ahora pongámosla en práctica. Codifiquemos una matriz de confusión con la biblioteca Scikit-learn (sklearn) en Python.

Sklearn tiene dos grandes funciones: matriz de confusión() y informe_clasificacion ().

• Sklearn matriz de confusión() devuelve los valores de la matriz de confusión. A pesar de esto, el resultado es ligeramente distinto de lo que hemos estudiado hasta el momento. Toma las filas como valores reales y las columnas como valores predichos. El resto del concepto sigue siendo el mismo.
• Sklearn informe_clasificacion () genera precisión, recuperación y puntuación f1 para cada clase objetivo. Al mismo tiempo de esto, además tiene algunos valores extra: micro promedio, promedio macro, y promedio ponderado

Promedio Mirco es la precisión / recuperación / puntuación f1 calculada para todas las clases.

Media macro es el promedio de precisión / recuerdo / puntuación f1.

Peso promedio es solo el promedio ponderado de precisión / recuperación / puntuación f1.

Matriz de confusión para clasificación de clases múltiples

¿Cómo funcionaría una matriz de confusión para un obstáculo de clasificación de clases múltiples? Bueno, ¡no te rasques la cabeza! Echaremos un vistazo a eso aquí.

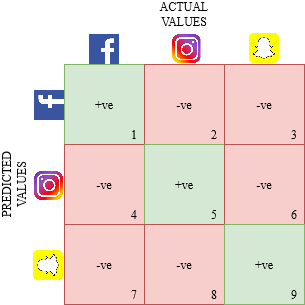
Dibujemos una matriz de confusión para un obstáculo multiclase donde tenemos que predecir si una persona ama Facebook, Instagram o Snapchat. La matriz de confusión sería una matriz de 3 x 3 como esta:

El verdadero positivo, verdadero negativo, falso positivo y falso negativo de cada clase se calcularía sumando los valores de celda de la próxima manera:

¡Eso es todo! ¡Está listo para descifrar cualquier matriz de confusión N x N!

Notas finales

¡Y de repente, la matriz de confusión ya no es tan confusa! Este post debería brindarle una base sólida acerca de cómo interpretar y utilizar una matriz de confusión para los algoritmos de clasificación en el aprendizaje automático.

Pronto publicaremos un post sobre la curva AUC-ROC y continuaremos nuestra discusión allí. Hasta la próxima, no pierda la esperanza en su modelo de clasificación, ¡es factible que esté usando la métrica de evaluación incorrecta!

Relacionado