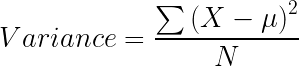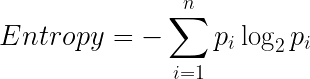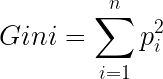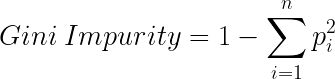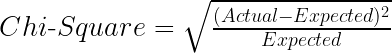Visión general
- ¿Cómo se divide un árbol de decisiones? ¿Cuáles son los diferentes criterios de división cuando se trabaja con árboles de decisión?
- Aprenda todo sobre los métodos de división del árbol de decisiones aquí y domine un popular algoritmo de aprendizaje automático
Introducción
Los árboles de decisión son sencillos de implementar e igualmente fáciles de interpretar. A menudo me apoyo en árboles de decisiones como mi algoritmo de aprendizaje automático, ya sea que esté comenzando un nuevo proyecto o compitiendo en un hackathon.
¡Y los árboles de decisión también son una idea para los recién llegados al aprendizaje automático! Pero las preguntas que debe hacer (y conocer la respuesta) son:
- ¿Cómo se divide un árbol de decisiones?
- ¿Cuáles son los diferentes criterios de división?
- ¿Cuál es la diferencia entre Gini y Information Gain?
Si no está seguro ni siquiera de una de estas preguntas, ¡ha venido al lugar correcto! Decision Tree es un poderoso algoritmo de aprendizaje automático que también sirve como base para otros algoritmos de aprendizaje automático complejos y ampliamente utilizados como Bosque aleatorio, XGBoost, y LightGBM. ¡Puedes imaginar por qué es importante aprender sobre este tema!
Las bibliotecas de programación de hoy en día han facilitado el uso de cualquier algoritmo de aprendizaje automático, pero esto tiene el costo de una implementación oculta, que es imprescindible para comprender completamente un algoritmo. Otra razón de esta lucha infinita es la disponibilidad de múltiples formas de dividir los nodos del árbol de decisión, lo que aumenta la confusión.
¿Alguna vez te has encontrado con esta lucha? ¿No pudo encontrar una solución? En este artículo, explicaré 4 métodos simples para dividir un nodoNodo es una plataforma digital que facilita la conexión entre profesionales y empresas en busca de talento. A través de un sistema intuitivo, permite a los usuarios crear perfiles, compartir experiencias y acceder a oportunidades laborales. Su enfoque en la colaboración y el networking hace de Nodo una herramienta valiosa para quienes desean expandir su red profesional y encontrar proyectos que se alineen con sus habilidades y objetivos.... en un árbol de decisión.
Asumo familiaridad con los conceptos básicos de regresión y árboles de decisión. Aquí hay dos cursos gratuitos y populares para aprender rápidamente o repasar los conceptos clave:
Terminologías básicas del árbol de decisiones
Revisemos rápidamente las terminologías clave relacionadas con los árboles de decisión que usaré a lo largo del artículo.
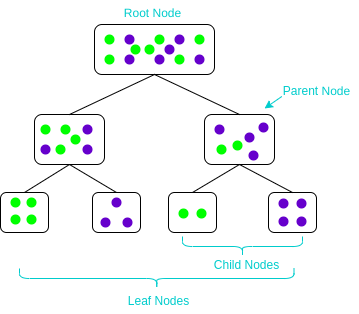
- Nodo padre e hijo: Un nodo que se divide en subnodos se conoce como nodo principal, y estos subnodos se conocen como nodos secundarios. Dado que un nodo se puede dividir en varios subnodos, un nodo puede actuar como nodo padre de numerosos nodos secundarios
- Nodo raíz: El nodo más alto de un árbol de decisiones. No tiene ningún nodo padre. Representa a toda la población o muestra
- Nodos hoja / terminal: Los nodos que no tienen ningún nodo hijo se conocen como nodos terminales / hoja
¿Qué es la división de nodos en un árbol de decisiones y por qué se realiza?
Antes de aprender cualquier tema, creo que es fundamental entender por qué lo estás aprendiendo. Eso ayuda a comprender el objetivo de aprender un concepto. Entonces, entendamos por qué aprender sobre la división de nodos en árboles de decisión.
Dado que todos saben cuán extensamente se utilizan los árboles de decisión, no se puede negar el hecho de que aprender acerca de los árboles de decisión es imprescindible. Un árbol de decisiones toma decisiones dividiendo los nodos en subnodos. Este proceso se realiza varias veces durante el proceso de entrenamiento hasta que solo quedan nodos homogéneos. Y es la única razón por la que un árbol de decisiones puede funcionar tan bien. Por lo tanto, la división de nodos es un concepto clave que todos deberían conocer.
La división de nodos, o simplemente la división, es el proceso de dividir un nodo en múltiples subnodos para crear nodos relativamente puros. Hay varias formas de hacer esto, que se pueden dividir en dos categorías según el tipo de variable de destino:
- Variable objetivo continua
- Variable objetivo categórica
- Impureza de Gini
- Ganancia de información
- Chi-cuadrado
En las próximas secciones, veremos cada método de división en detalle. Comencemos con el primer método de división: reducción de la varianza.
Método de división del árbol de decisión n. ° 1: reducción de la varianza
La reducción de la varianza es un método para dividir el nodo que se utiliza cuando la variable objetivo es continua, es decir, problemas de regresión. Se llama así porque utiliza la varianza como una medida para decidir la característica en qué nodo se divide en nodos secundarios.
La varianza se utiliza para calcular la homogeneidad de un nodo. Si un nodo es completamente homogéneo, entonces la varianza es cero.
Estos son los pasos para dividir un árbol de decisiones mediante la reducción de la varianza:
- Para cada división, calcule individualmente la varianza de cada nodo hijo
- Calcule la varianza de cada división como la varianza promedio ponderada de los nodos secundarios
- Seleccione la división con la varianza más baja
- Realice los pasos del 1 al 3 hasta lograr nodos completamente homogéneos.
El siguiente video explica de manera excelente la reducción en la varianza usando un ejemplo:
Método de división del árbol de decisión n. ° 2: ganancia de información
Ahora, ¿qué pasa si tenemos una variableEn estadística y matemáticas, una "variable" es un símbolo que representa un valor que puede cambiar o variar. Existen diferentes tipos de variables, como las cualitativas, que describen características no numéricas, y las cuantitativas, que representan cantidades numéricas. Las variables son fundamentales en experimentos y estudios, ya que permiten analizar relaciones y patrones entre diferentes elementos, facilitando la comprensión de fenómenos complejos.... objetivo categórica? La reducción de la variación no será suficiente.
Bueno, la respuesta es ganancia de información. La ganancia de información se utiliza para dividir los nodos cuando la variable objetivo es categórica. Funciona sobre el concepto de entropía y viene dado por:
La entropía se utiliza para calcular la pureza de un nodo. Cuanto menor sea el valor de la entropía, mayor es la pureza del nodo. La entropía de un nodo homogéneo es cero. Como restamos la entropía de 1, la ganancia de información es mayor para los nodos más puros con un valor máximo de 1. Ahora, echemos un vistazo a la fórmula para calcular la entropía:
Pasos para dividir un árbol de decisiones utilizando la ganancia de información:
- Para cada división, calcule individualmente la entropía de cada nodo hijo
- Calcule la entropía de cada división como la entropía promedio ponderada de los nodos secundarios
- Seleccione la división con la entropía más baja o la ganancia de información más alta
- Hasta que logre nodos homogéneos, repita los pasos 1-3
Aquí hay un video sobre cómo usar la ganancia de información para dividir un árbol de decisiones:
Método de división del árbol de decisión # 3: Impureza de Gini
Gini Impurity es un método para dividir los nodos cuando la variable objetivo es categórica. Es la forma más popular y sencilla de dividir un árbol de decisiones. El valor de la impureza de Gini es:
Espera, ¿qué es Gini?
Gini es la probabilidad de etiquetar correctamente un elemento elegido al azar si se etiquetó al azar de acuerdo con la distribución de etiquetas en el nodo. La fórmula de Gini es:
Y Gini Impurity es:
Cuanto menor sea la impureza de Gini, mayor es la homogeneidad del nodo. La impureza de Gini de un nodo puro es cero. Ahora, podría estar pensando que ya sabemos acerca de la ganancia de información, entonces, ¿por qué necesitamos Gini Impureza?
Se prefiere la impureza de Gini a la ganancia de información porque no contiene logaritmos que sean computacionalmente intensivos.
Estos son los pasos para dividir un árbol de decisiones usando Gini Impurity:
- Similar a lo que hicimos en la obtención de información. Para cada división, calcule individualmente la impureza de Gini de cada nodo hijo
- CCalcule la Impureza de Gini de cada división como la Impureza de Gini promedio ponderada de los nodos secundarios.
- Seleccione la división con el valor más bajo de Gini Impureza
- Hasta que logre nodos homogéneos, repita los pasos 1-3
Y aquí está Gini Impurity en forma de video:
Método de división del árbol de decisión # 4: Chi-cuadrado
Chi-cuadrado es otro método de dividir nodos en un árbol de decisión para conjuntos de datos que tienen valores objetivo categóricos. Puede hacer dos o más de dos divisiones. Trabaja en la significación estadística de las diferencias entre el nodo padre y los nodos secundarios.
El valor de chi-cuadrado es:
Aquí el Esperado es el valor esperado para una clase en un nodo hijo basado en la distribución de clases en el nodo padre, y Real es el valor real de una clase en un nodo hijo.
La fórmula anterior nos da el valor de Chi-Cuadrado para una clase. Tome la suma de los valores de Chi-Cuadrado para todas las clases en un nodo para calcular el Chi-Cuadrado para ese nodo. Cuanto mayor sea el valor, mayores serán las diferencias entre los nodos padre e hijo, es decir, mayor será la homogeneidad.
Estos son los pasos para dividir un árbol de decisiones usando Chi-Cuadrado:
- Para cada división, calcule individualmente el valor de Chi-Cuadrado de cada nodo hijo tomando la suma de los valores de Chi-Cuadrado para cada clase en un nodo.
- Calcule el valor de Chi-Cuadrado de cada división como la suma de los valores de Chi-Cuadrado para todos los nodos secundarios
- Seleccione la división con mayor valor de chi-cuadrado
- Hasta que logre nodos homogéneos, repita los pasos 1-3
Por supuesto, hay un video que explica Chi-Cuadrado en el contexto de un árbol de decisiones:
Notas finales
Ahora, conoce los diferentes métodos para dividir un árbol de decisiones. En los siguientes pasos, puede ver nuestro lista de reproducción completa sobre árboles de decisión en youtube. O puede tomar nuestro gratis curso sobre árboles de decisión aquí.
También he reunido una lista de artículos fantásticos sobre árboles de decisiones a continuación:
Si este artículo le pareció informativo, compártalo con sus amigos y comente a continuación con sus consultas o pensamientos.
Relacionado
Posts Relacionados:
- Clasificación del árbol de decisión | Guía para la clasificación del árbol de decisiones
- Árbol de decisiones de Weka | Cree un árbol de decisiones con Weka
- Algoritmo de árbol de decisión para clasificación: aprendizaje automático 101
- Impureza de Gini | División de árboles de decisión con impureza de Gini