Big Data

Modelado estadístico | Introducción al modelado estadístico

Este artículo fue publicado como parte del Blogatón de ciencia de datos.

¿Qué es un modelo estadístico?

«El modelado es un arte, así como una ciencia, y está dirigido a encontrar un buen modelo aproximado … como base para la inferencia estadística» – Burnham & Anderson

Un modelo estadístico es un tipo de modelo matemático que forma parte de la supuestos realizado para describir el proceso de generación de datos.

Centrémonos en los dos términos resaltados arriba:

¿Tipo de modelo matemático? El modelo estadístico no es determinista a diferencia de otros modelos matemáticos donde las variables tienen valores específicos. Las variables en los modelos estadísticos son estocásticas, es decir, tienen distribuciones de probabilidad.
¿Supuestos? Pero, ¿cómo nos ayudan esos supuestos a comprender las propiedades o características de los datos verdaderos? En pocas palabras, estos supuestos facilitan el cálculo de la probabilidad de un evento.

Cotización un ejemplo para comprender mejor el papel de los supuestos estadísticos en el modelado de datos:

Supuesto 1: Suponiendo que tenemos 2 dados justos y que cada cara tiene la misma probabilidad de aparecer, es decir, 1/6. Ahora, podemos calcular la probabilidad de que dos dados muestren 5 como 1/6 * 1/6. Como podemos calcular la probabilidad de cada evento, constituye un modelo estadístico.

Supuesto 2: Los dados están ponderados y todo lo que sabemos es que la probabilidad de la cara 5 es 1/8, lo que facilita el cálculo de la probabilidad de que ambos dados muestren 5 como 1/8 * 1/8. Pero no conocemos la probabilidad de otras caras, por lo que no podemos calcular la probabilidad de cada evento. Por tanto, este supuesto no constituye un modelo estadístico.

¿Por qué necesitamos el modelado estadístico?

El modelo estadístico juega un papel fundamental en la realización de inferencias estadísticas que ayudan a hacer proposiciones sobre las propiedades y características desconocidas de la población como se muestra a continuación:

1) Estimacion:

Es la idea central detrás del aprendizaje automático, es decir, averiguar el número que puede estimar los parámetrosLos "parámetros" son variables o criterios que se utilizan para definir, medir o evaluar un fenómeno o sistema. En diversos campos como la estadística, la informática y la investigación científica, los parámetros son fundamentales para establecer normas y estándares que guían el análisis y la interpretación de datos. Su adecuada selección y manejo son cruciales para obtener resultados precisos y relevantes en cualquier estudio o proyecto.... de distribución.

Tenga en cuenta que el estimadorEl "Estimador" es una herramienta estadística utilizada para inferir características de una población a partir de una muestra. Se basa en métodos matemáticos para proporcionar estimaciones precisas y confiables. Existen diferentes tipos de estimadores, como los insesgados y los consistentes, que se eligen según el contexto y el objetivo del estudio. Su correcto uso es fundamental en investigaciones científicas, encuestas y análisis de datos.... es una variableEn estadística y matemáticas, una "variable" es un símbolo que representa un valor que puede cambiar o variar. Existen diferentes tipos de variables, como las cualitativas, que describen características no numéricas, y las cuantitativas, que representan cantidades numéricas. Las variables son fundamentales en experimentos y estudios, ya que permiten analizar relaciones y patrones entre diferentes elementos, facilitando la comprensión de fenómenos complejos.... aleatoria en sí mismo, mientras que una estimación es un número único que nos da una idea de la distribución del proceso de generación de datos. Por ejemplo, la media y sigma de la distribución gaussiana

2) Intervalo de confianza:

Da una barra de error alrededor del número de estimación única, es decir, un rango de valores para indicar la confianza en la estimación obtenida sobre la base de varias muestras. Por ejemplo, la estimación A se calcula a partir de 100 muestras y tiene un intervalo de confianza más amplio, mientras que la estimación B se calcula a partir de 10000 muestras y, por lo tanto, tiene un intervalo de confianza más estrecho.

3) Prueba de hipótesis

Es una declaración de búsqueda de evidencia estadística. Comprendamos mejor la necesidad de realizar modelos estadísticos con la ayuda de un ejemplo a continuación.

51737research_paers-2486221 — Fuente: Autor

El objetivo es comprender la distribución subyacente para calcular la probabilidad de que un investigador seleccionado al azar hubiera escrito, digamos, 3 artículos de investigación.

Tenemos una variable aleatoria discreta con 8 (9-1) parámetros para aprender, es decir, probabilidad de 0,1,2 .. trabajos de investigación. A medidaLa "medida" es un concepto fundamental en diversas disciplinas, que se refiere al proceso de cuantificar características o magnitudes de objetos, fenómenos o situaciones. En matemáticas, se utiliza para determinar longitudes, áreas y volúmenes, mientras que en ciencias sociales puede referirse a la evaluación de variables cualitativas y cuantitativas. La precisión en la medición es crucial para obtener resultados confiables y válidos en cualquier investigación o aplicación práctica.... que aumenta el número de parámetros a estimar, también lo es la necesidad de tener tantas observaciones, pero este no es el propósito del modelado de datos.

Entonces, podemos reducir el número de incógnitas de 8 parámetros a solo 1 parámetro lambda, simplemente asumiendo que los datos siguen la distribución de Poisson.

Nuestra suposición de que los datos siguen la distribución de Poisson podría ser una simplificación en comparación con el proceso de generación de datos reales, pero es una buena aproximación.

Tipos de supuestos de modelado:

Ahora que entendemos la importancia del modelado estadístico, entendamos el tipos de supuestos de modelado:

1) Paramétrico: Asume un conjunto finito de parámetros que capturan todo lo relacionado con los datos. Si conocemos el parámetro θ que encarna muy bien el proceso de generación de datos, entonces las predicciones (x) son independientes de los datos observados (D)

2) No paramétrico: Supone que ningún conjunto finito de parámetros puede definir la distribución de datos. La complejidad del modelo es ilimitada y crece con la cantidad de datos

3) Semiparamétrico: Es un modelo híbrido cuyos supuestos se encuentran entre enfoques paramétricos y no paramétricos. Consta de dos componentes: estructural (paramétrico) y variación aleatoria (no paramétrico). El modelo de riesgo proporcional de Cox es un ejemplo popular de supuestos semiparamétricos.

Definición de un modelo estadístico: (S, P)

S: Supongamos que tenemos una colección de copias N iid como X1, X2, X3… Xn a través de un experimento estadístico (es el proceso de generar o recolectar datos). Todos estos Las variables aleatorias se pueden medir en un espacio muestral que se denota por S.

PAG: Es el conjunto de distribuciones de probabilidad en S que contiene la distribución que es una representación aproximada de nuestra distribución real.

Internalicemos el concepto de espacio muestral antes de comprender cómo se podría representar un modelo estadístico para estas distribuciones.

1) Bernoulli: {0,1}

2) Gaussiano: (-∞, + ∞)

Entonces, ahora hemos visto algunos ejemplos de espacio muestral de algunas de las familias de la distribución, ahora veamos cómo se define un modelo estadístico:

1) Bernoulli: ({0,1}, (Ber (p)) p∈ (0,1))

2) Gaussiano: ((-∞, + ∞), (N (𝜇, 0.3)) 𝜇∈R)

Bueno, modelos especificados y mal especificados:

¿Qué es la especificación del modelo? Según Wikipedia definición:

Especificación del modelo consiste en seleccionar una forma funcional adecuada para el modelo. Por ejemplo, dado «ingreso personal» (y) junto con «años de escolaridad» (s) y «experiencia en el trabajo» (x), podríamos especificar una relación funcional y = f (s, x)} como sigue:

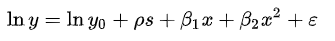
Modelo de especificación incorrecta: ¿Alguna vez le ha sucedido que el modelo converge correctamente en datos simulados, pero en el momento en que llegan los datos reales, su robustez se degrada y ya no converge? Bueno, esto podría suceder normalmente si el modelo que desarrolló no coincide con los datos, lo que generalmente se conoce como Modelo de especificación incorrecta. Podría deberse a que la clase de distribución asumida para el modelado no contiene la distribución de probabilidad desconocida p de donde se extrae la muestra, es decir, el verdadero proceso de generación de datos.

Fuente: Autor

Espero que este artículo le haya dado una comprensión de qué es un modelo estadístico, por qué necesitamos tales modelos, qué papel juegan los supuestos y cómo pueden esos supuestos decidir la bondad de nuestro modelo.

*El proceso de distribución / generación de datos real o real al que se hace referencia a lo largo de este artículo implica que existe una distribución de probabilidad que es inducida por el proceso que genera los datos observados.