Introducción
En este artículo, aprenderemos los conceptos de gestión de carteras e implementaremos los mismos mediante el uso de bibliotecas de Python.
El artículo se divide en tres partes con el fin de cubrir los aspectos fundamentales de la gestión de carteras como se muestra a continuación:
1. Rentabilidad de un activo y una cartera
2. Riesgo asociado con un activo y una cartera
3. Teoría moderna de la cartera: encontrar la cartera óptima
Rentabilidad de un activo y una cartera
Antes de sumergirnos en el cálculo de los rendimientos de un activo y una cartera, visitemos brevemente la definición de cartera y rendimientos.
portafolio: Una cartera es una colección de instrumentos financieros como acciones, bonos, materias primas, efectivo y equivalentes de efectivo, así como sus contrapartes de fondos. [Investopedia]
En este artículo, tendremos nuestra cartera que contiene 4 activos (“Cartera centrada en acciones“): Las acciones de Apple Inc., Nike (NKC), Google y Amazon. La vista previa de nuestros datos se muestra a continuación:
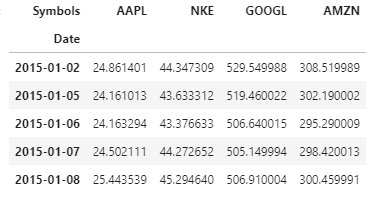
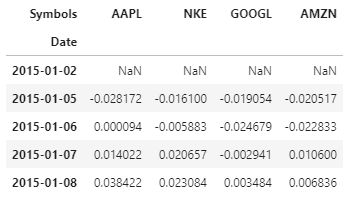
Devoluciones: Se refiere a la ganancia o pérdida de nuestro activo / cartera durante un período de tiempo fijo. En este análisis, hacemos un retorno como el cambio porcentual en el precio de cierre del activo sobre el precio de cierre del día anterior. Calcularemos los rendimientos usando.pct_change () función en python.
A continuación se muestra el código de Python para hacer lo mismo y las 5 filas superiores (encabezado) de las devoluciones
Nota: la primera fila es Nula si no existe una fila anterior para facilitar el cálculo del cambio porcentual.
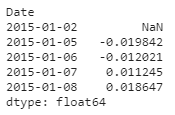
Devolución de una cartera se define como la suma ponderada de los rendimientos de los activos de la cartera.
Para demostrar cómo calcular el rendimiento de la cartera en Python, inicialicemos los pesos de forma aleatoria (que luego optimizaremos). El rendimiento de la cartera se calcula como se muestra en el código a continuación y también se muestra el encabezado de los rendimientos de la cartera:
Hemos visto cómo calcular los rendimientos, ahora cambiemos nuestro enfoque a otro concepto: Riesgo
El riesgo asociado con los activos y la cartera
El método para calcular el riesgo de una cartera se escribe a continuación y posteriormente explicamos y damos la formulación matemática para cada uno de los pasos:
- Calcule la matriz de covarianza en los datos de rendimiento.
- Anualice la covarianza multiplicando por 252
- Calcule la varianza de la cartera multiplicándola con vectores de peso.
- Calcule la raíz cuadrada de la varianza calculada anteriormente para obtener la desviación estándar. Esta desviación estándar se denomina Volatilidad de la cartera.
La fórmula para calcular la covarianza y anualizarla es:
covarianza = devuelve.cov () * 252
como hay 252 días hábiles, multiplicamos la covarianza por 252 para anualizarla.
La variación de la cartera, que se calculará en el paso 3 anterior, depende de los pesos de los activos en la cartera y se define como:
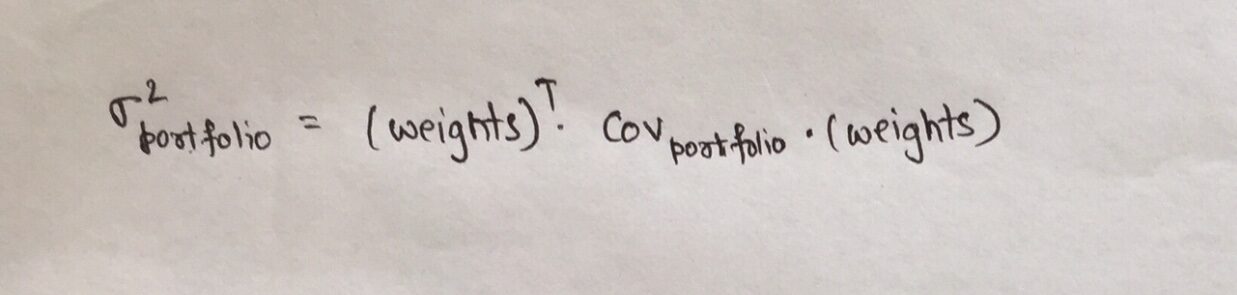
dónde,
- Covportafolio es la matriz de covarianza de la cartera
- ponderaciones es el vector de ponderaciones asignadas a cada activo de la cartera
A continuación se muestra el enfoque para calcular el riesgo de activos en Python.
Como se explicó anteriormente, multiplicamos la matriz de covarianza con 252, ya que hay 252 días de negociación en un año.
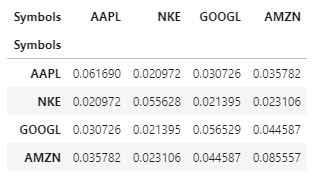
Los elementos diagonales de varnce_matrix representan la varianza de cada activo, mientras que los términos fuera de la diagonal representan la covarianza entre los dos activos, por ejemplo: el elemento (1,2) representa la covarianza entre Nike y Apple.
El código para calcular el riesgo de la cartera en python, cuyo método vimos anteriormente, es como se muestra:
Ahora, la tarea para nosotros es optimizar los pesos. ¿Por qué? Para que podamos maximizar nuestro rendimiento o minimizar nuestro riesgo, ¡y eso lo hacemos utilizando la teoría de la cartera moderna!
Teoría moderna de la cartera
La teoría moderna de la cartera sostiene que las características de riesgo y rendimiento de una inversión no deben considerarse solas, sino que deben evaluarse según la forma en que la inversión afecta el riesgo y el rendimiento general de la cartera. MPT muestra que un inversor puede construir una cartera de múltiples activos que maximizará los rendimientos para un nivel de riesgo determinado. Asimismo, dado un nivel deseado de rendimiento esperado, un inversor puede construir una cartera con el menor riesgo posible. Basado en medidas estadísticas como la varianza y la correlación, el desempeño de un inversionista individual es menos importante que cómo impacta a toda la cartera. [Investopedia]
Esta teoría se resume en la siguiente figura"Figura" es un término que se utiliza en diversos contextos, desde el arte hasta la anatomía. En el ámbito artístico, se refiere a la representación de formas humanas o animales en esculturas y pinturas. En la anatomía, designa la forma y estructura del cuerpo. Además, en matemáticas, "figura" se relaciona con las formas geométricas. Su versatilidad hace que sea un concepto fundamental en múltiples disciplinas..... Encontramos la frontera como se muestra a continuación y maximizamos el rendimiento esperado para el nivel de riesgo o minimizamos el riesgo para un nivel de rendimiento esperado determinado.
Nuestro objetivo es elegir las ponderaciones para cada activo de nuestra cartera de modo que maximicemos el rendimiento esperado dado un nivel de riesgo.
Matemáticamente, la función objetivo se puede definir como se muestra a continuación:
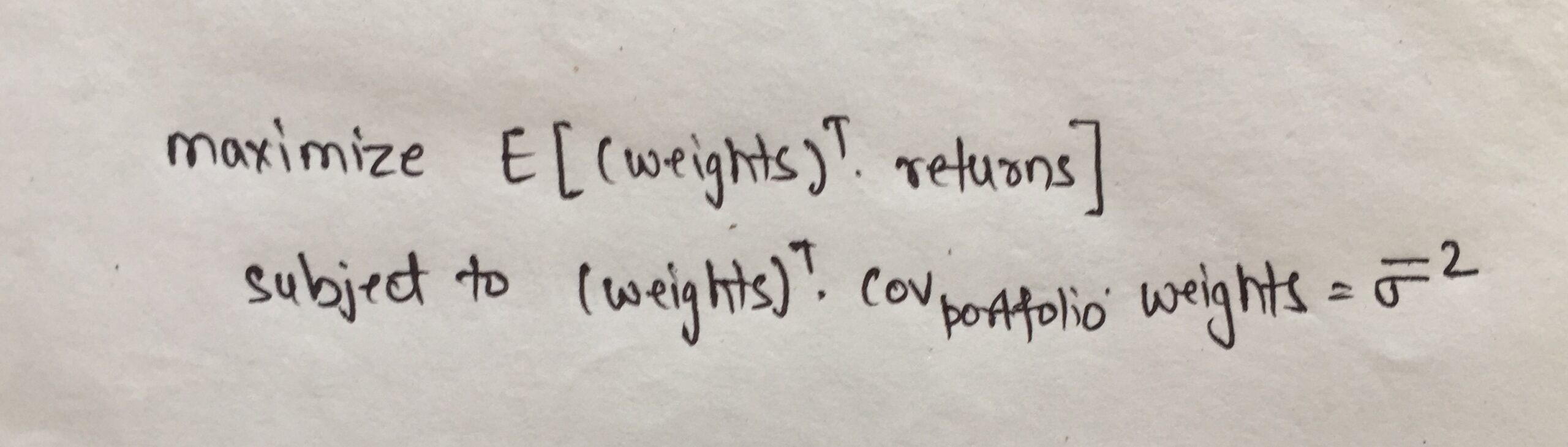
Otra forma de ver la Frontera Eficiente y la función objetivo es que podemos minimizar el riesgo dado que el rendimiento esperado es al menos mayor que el valor dado. Matemáticamente, esta función objetivo se puede escribir como:
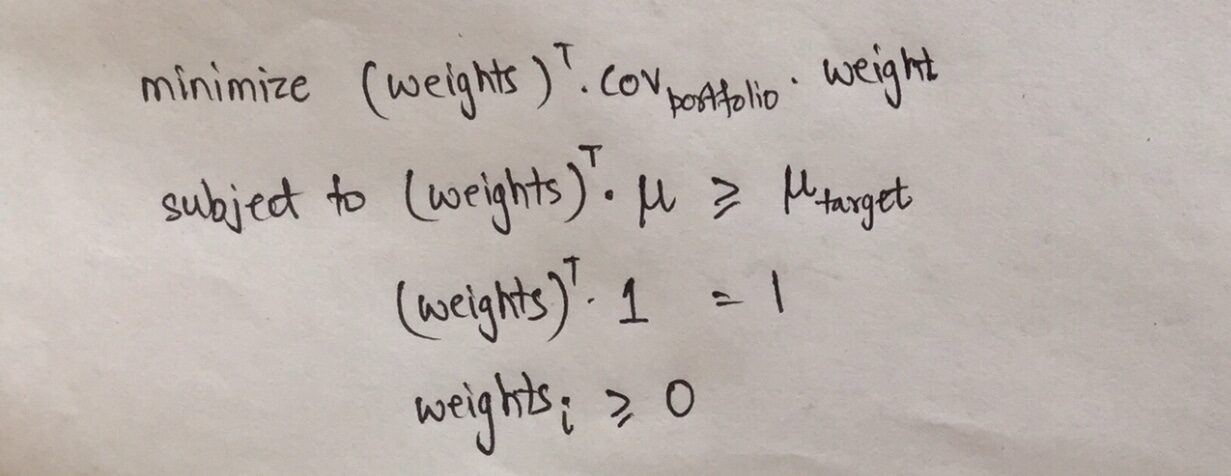
la primera línea representa que el objetivo es minimizar la varianza de la cartera, es decir, a su vez la volatilidad de la cartera y, por tanto, minimizar el riesgo.
El sujeto a restricciones implica que los rendimientos deben ser mayores que un rendimiento objetivo en particular, todas las ponderaciones deben sumar 1 y las ponderaciones no deben ser negativas.
Ahora que conocemos el concepto, ¡pasemos a la parte práctica ahora!
En primer lugar, creamos la frontera eficiente ejecutando un bucle. En cada ciclo, consideramos un conjunto diferente de ponderaciones asignadas aleatoriamente para los activos de nuestra cartera y calculamos el rendimiento y la volatilidad para esa combinación de ponderaciones.
Para ello creamos 3 listas vacías, una para almacenar los rendimientos, otra para almacenar la volatilidad y la última para almacenar los pesos de la cartera.
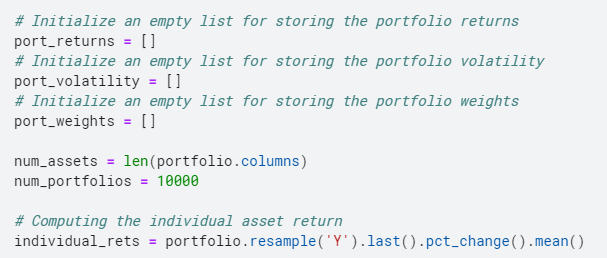
Una vez que hemos creado las listas, generamos aleatoriamente las ponderaciones de nuestros activos repetidamente, luego normalizamos la ponderación para sumar 1. Luego calculamos los rendimientos de la misma manera que calculamos anteriormente. Posteriormente, calculamos la varianza de la cartera y luego sacamos la raíz cuadrada y luego la anualizamos para obtener la volatilidad, la medidaLa "medida" es un concepto fundamental en diversas disciplinas, que se refiere al proceso de cuantificar características o magnitudes de objetos, fenómenos o situaciones. En matemáticas, se utiliza para determinar longitudes, áreas y volúmenes, mientras que en ciencias sociales puede referirse a la evaluación de variables cualitativas y cuantitativas. La precisión en la medición es crucial para obtener resultados confiables y válidos en cualquier investigación o aplicación práctica.... de riesgo para nuestra cartera.
Ahora agregamos los datos en un diccionario y luego creamos un marco de datos para ver la combinación de ponderaciones de los activos y los rendimientos correspondientes y la volatilidad que generan.
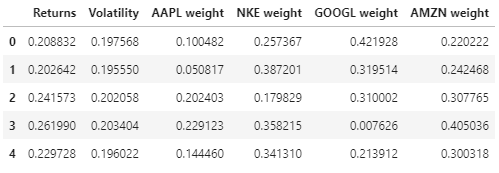
Aquí está la vista previa de los datos de rentabilidad, volatilidad y ponderaciones de la cartera.
¡Ahora tenemos todo con nosotros para entrar en la última vuelta de esta carrera y encontrar el juego de pesos óptimo!
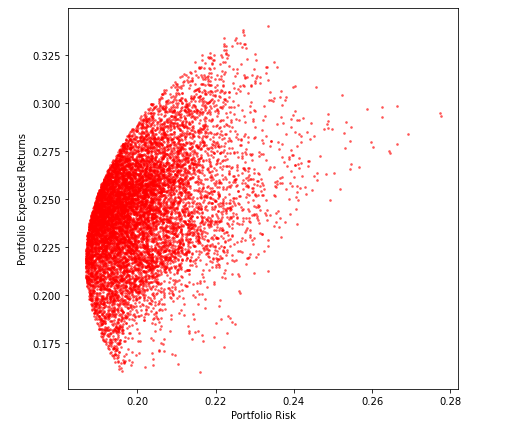
Trazamos la Volatilidad contra los rendimientos que calculamos anteriormente, esto nos dará la Frontera Eficiente que queríamos crear al principio de este artículo.
¡¡Y aquí vamos!!
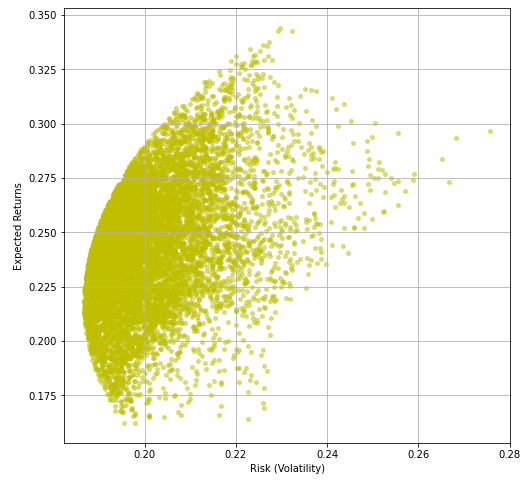
Ahora que tenemos con nosotros la Frontera Eficiente, busquemos los pesos óptimos.
Podemos optimizar el uso de varios métodos como se describe a continuación:
- Cartera con mínima volatilidad (riesgo)
- Cartera óptima (relación máxima de Sharpe)
- Rentabilidad máxima a nivel de riesgo; Riesgo mínimo a un nivel de rendimiento esperado; Cartera con mayor ratio de Sortino
En este artículo optimizaré a través de los dos primeros enfoques. En el tercer segmento, el ‘Rendimiento máximo a un nivel de riesgo’ y el ‘Riesgo mínimo a un nivel de rendimiento esperado’ son bastante sencillos, mientras que el que se basa en el índiceEl "Índice" es una herramienta fundamental en libros y documentos, que permite ubicar rápidamente la información deseada. Generalmente, se presenta al inicio de una obra y organiza los contenidos de manera jerárquica, incluyendo capítulos y secciones. Su correcta elaboración facilita la navegación y mejora la comprensión del material, convirtiéndolo en un recurso esencial tanto para estudiantes como para profesionales en diversas áreas.... de Sortino es similar al índice de Sharpe.
1. Volatilidad mínima
Para encontrar la combinación de volatilidad mínima, seleccionamos la fila en nuestro marco de datos que corresponde a la varianza mínima y encontramos esa fila usando la función .idxmin (). El código para hacer lo mismo se muestra a continuación:
Los pesos que obtenemos de esto son:
Ahora, averigüe dónde se encuentra el punto mínimo de volatilidad en la curva anterior. ¡La respuesta se muestra al final! ¡Pero no hagas trampa!
2. Relación de nitidez más alta
El índice de Sharpe es el rendimiento promedio obtenido en exceso de la tasa libre de riesgo por unidad de volatilidad o riesgo total. La fórmula utilizada para calcular la relación de Sharpe se proporciona a continuación:
Relación de nitidez = (Rpag – RF)/ DAKOTA DEL SURpag
dónde,
- Rpag es el retorno de la cartera
- RF es la tasa libre de riesgo
- Dakota del Surpag es la desviación estándar de los rendimientos de la cartera
El código para calcular la cartera más óptima, es decir, la cartera con el índice de Sharpe más alto, se muestra a continuación:
A continuación, se muestran los pesos de la cartera que dan el índice de Sharpe más alto:
Averigüe dónde se encuentra el punto de relación de Sharpe más alto en la curva anterior. ¡La respuesta se muestra a continuación! Una vez más, ¡no hagas trampa!
¡Como se prometió aquí está la respuesta a las dos preguntas anteriores!
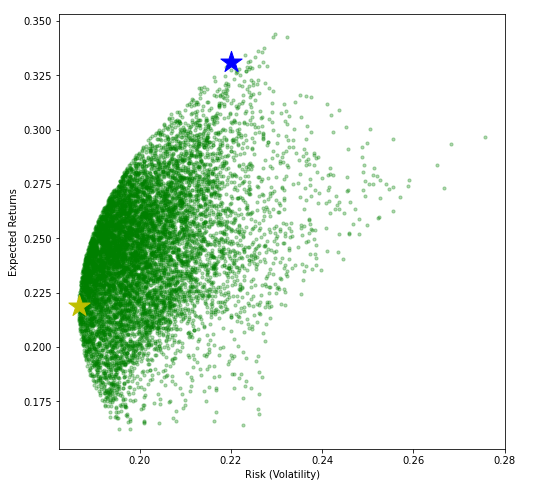
La estrella azul corresponde al punto de relación de Sharpe más alto y la estrella amarilla corresponde al punto de volatilidad mínima.
Ahora, antes de terminar este artículo, le animo a encontrar la cartera de Rentabilidad Máxima a un nivel de riesgo ‘y’ Riesgo Mínimo a un Nivel de Rentabilidad Esperada ‘y marcarlos en el gráfico anterior.
Además de utilizar la relación de Sharpe, también podemos optimizar la cartera utilizando la relación de Sortino.
Dando un breve al respecto:
los Relación de Sortino es una variación del índice de Sharpe que diferencia la volatilidad dañina de la volatilidad general total mediante el uso de la desviación estándar del activo de los rendimientos negativos de la cartera (desviación a la baja) en lugar de la desviación estándar total de los rendimientos de la cartera. La relación de Sortino toma el rendimiento de un activo o cartera y resta la tasa libre de riesgo, y luego divide esa cantidad por la desviación a la baja del activo. [Investopedia]
Relación de Sortino = (Rpag – rF)/ DAKOTA DEL SURD
dónde,
- Rpag es el retorno de la cartera
- rF es la tasa libre de riesgo
- Dakota del SurD es la desviación estándar de la desventaja
En caso de que tenga algún problema para implementar o comprender los 3 métodos de optimización que describí anteriormente, escríbame al [email protected] | [email protected] | o comuníquese con LinkedIn en https://www.linkedin.com/in/parth-tyagi-4b867452/
Nota sobre el autor: Parth Tyagi está actualmente cursando PGDBA de IIM Calcuta, IIT Kharagpur & Indian Statistical Institute-Kolkata y ha completado el B.Tech de IIT Delhi. Tiene ~ 4 años de experiencia laboral en análisis avanzado.
Los medios que se muestran en este artículo sobre la optimización de la cartera en Python no son propiedad de DataPeaker y se utilizan a discreción del autor.
