Este artículo fue publicado como parte del Blogatón de ciencia de datos
Los diversos métodos de aprendizaje profundoEl aprendizaje profundo, una subdisciplina de la inteligencia artificial, se basa en redes neuronales artificiales para analizar y procesar grandes volúmenes de datos. Esta técnica permite a las máquinas aprender patrones y realizar tareas complejas, como el reconocimiento de voz y la visión por computadora. Su capacidad para mejorar continuamente a medida que se le proporcionan más datos la convierte en una herramienta clave en diversas industrias, desde la salud... utilizan datos para entrenar algoritmos de redes neuronales para realizar una variedad de tareas de aprendizaje automático, como la clasificación de diferentes clases de objetos. Las redes neuronales convolucionales son algoritmos de aprendizaje profundo muy poderosos para el análisis de imágenes. Este artículo le explicará cómo construir, entrenar y evaluar redes neuronales convolucionales.
También aprenderá cómo mejorar su capacidad para aprender de los datos y cómo interpretar los resultados de la capacitación. El Deep Learning tiene varias aplicaciones como procesamiento de imágenes, procesamiento de lenguaje natural, etc. También se usa en Ciencias Médicas, Medios y Entretenimiento, Autos Autónomos, etc.
¿Qué es CNN?
CNN es un poderoso algoritmo para el procesamiento de imágenes. Estos algoritmos son actualmente los mejores algoritmos que tenemos para el procesamiento automatizado de imágenes. Muchas empresas utilizan estos algoritmos para hacer cosas como identificar los objetos en una imagen.
Las imágenes contienen datos de combinación RGB. Matplotlib se puede utilizar para importar una imagen a la memoria desde un archivo. La computadora no ve una imagen, todo lo que ve es una matriz de números. Las imágenes en color se almacenan en matrices tridimensionales. Las dos primeras dimensiones corresponden a la altura y el ancho de la imagen (el número de píxeles). La última dimensión"Dimensión" es un término que se utiliza en diversas disciplinas, como la física, la matemática y la filosofía. Se refiere a la medida en la que un objeto o fenómeno puede ser analizado o descrito. En física, por ejemplo, se habla de dimensiones espaciales y temporales, mientras que en matemáticas puede referirse a la cantidad de coordenadas necesarias para representar un espacio. Su comprensión es fundamental para el estudio y... corresponde a los colores rojo, verde y azul presentes en cada píxel.
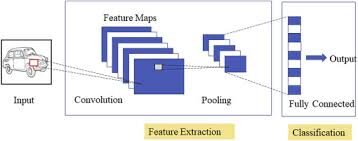
Tres capas de CNN
Redes neuronales convolucionales especializadas para aplicaciones en reconocimiento de imagen y video. CNN se utiliza principalmente en tareas de análisis de imágenes como reconocimiento de imágenes, detección de objetos y segmentaciónLa segmentación es una técnica clave en marketing que consiste en dividir un mercado amplio en grupos más pequeños y homogéneos. Esta práctica permite a las empresas adaptar sus estrategias y mensajes a las características específicas de cada segmento, mejorando así la eficacia de sus campañas. La segmentación puede basarse en criterios demográficos, psicográficos, geográficos o conductuales, facilitando una comunicación más relevante y personalizada con el público objetivo.....
Hay tres tipos de capas en las redes neuronales convolucionales:
1) Capa convolucionalLa capa convolucional, fundamental en las redes neuronales convolucionales (CNN), se utiliza principalmente para el procesamiento de datos con estructuras en forma de cuadrícula, como imágenes. Esta capa aplica filtros que extraen características relevantes, como bordes y texturas, permitiendo que el modelo reconozca patrones complejos. Su capacidad para reducir la dimensionalidad de los datos y mantener información esencial la convierte en una herramienta clave en tareas de visión por computadora...: en una red neuronalLas redes neuronales son modelos computacionales inspirados en el funcionamiento del cerebro humano. Utilizan estructuras conocidas como neuronas artificiales para procesar y aprender de los datos. Estas redes son fundamentales en el campo de la inteligencia artificial, permitiendo avances significativos en tareas como el reconocimiento de imágenes, el procesamiento del lenguaje natural y la predicción de series temporales, entre otros. Su capacidad para aprender patrones complejos las hace herramientas poderosas... típica, cada neurona de entrada está conectada a la siguiente capa oculta. En CNN, solo una pequeña región de las neuronas de la capa de entradaLa "capa de entrada" se refiere al nivel inicial en un proceso de análisis de datos o en arquitecturas de redes neuronales. Su función principal es recibir y procesar la información bruta antes de que esta sea transformada por capas posteriores. En el contexto de machine learning, una adecuada configuración de la capa de entrada es crucial para garantizar la efectividad del modelo y optimizar su rendimiento en tareas específicas.... se conecta a la capa oculta de neuronas.
2) Capa de agrupación: la capa de agrupación se utiliza para reducir la dimensionalidad del mapa de características. Habrá múltiples capas de activación y agrupación dentro de la capa oculta de la CNN.
3) Capa completamente conectada: Capas completamente conectadas formar los últimos capas en la red. La entrada al capa completamente conectada es la salida de la agrupación o convolución final Capa, que se aplana y luego se introduce en el capa completamente conectada.
Conjunto de datos MNIST
En este artículo, trabajaremos en el reconocimiento de objetos en datos de imágenes utilizando el conjunto de datos MNIST para el reconocimiento de dígitos escritos a mano.
El conjunto de datos MNIST consta de imágenes de dígitos de una variedad de documentos escaneados. Cada imagen es un cuadrado de 28 x 28 píxeles. En este conjunto de datos, se utilizan 60.000 imágenes para entrenar el modelo y 10.000 imágenes para probar el modelo. Hay 10 dígitos (0 a 9) o 10 clases para predecir.

Cargando el conjunto de datos MNIST
Instale la biblioteca de TensorFlow e importe el conjunto de datos como un conjunto de datos de entrenamientoEl entrenamiento es un proceso sistemático diseñado para mejorar habilidades, conocimientos o capacidades físicas. Se aplica en diversas áreas, como el deporte, la educación y el desarrollo profesional. Un programa de entrenamiento efectivo incluye la planificación de objetivos, la práctica regular y la evaluación del progreso. La adaptación a las necesidades individuales y la motivación son factores clave para lograr resultados exitosos y sostenibles en cualquier disciplina.... y prueba.
Trazar la salida de muestra de la imagen
!pip install tensorflow
from keras.datasets import mnist
import matplotlib.pyplot as plt
(X_train,y_train), (X_test, y_test)= mnist.load_data()
plt.subplot()
plt.imshow(X_train[9], cmap=plt.get_cmap('gray'))
Producción:
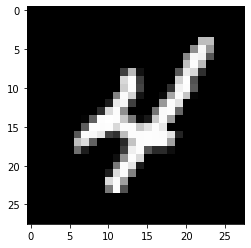
Modelo de aprendizaje profundo con perceptrones multicapa utilizando MNIST
En este modelo, crearemos un modelo de red neuronal simple con una sola capa oculta para el conjunto de datos MNIST para el reconocimiento de dígitos escritos a mano.
Un perceptrón es un modelo de neurona única que es el componente básico de las redes neuronales más grandes. El perceptrón multicapa consta de tres capas, es decir, la capa de entrada, la capa oculta y la capa de salidaLa "capa de salida" es un concepto utilizado en el ámbito de la tecnología de la información y el diseño de sistemas. Se refiere a la última capa de un modelo de software o arquitectura que se encarga de presentar los resultados al usuario final. Esta capa es crucial para la experiencia del usuario, ya que permite la interacción directa con el sistema y la visualización de datos procesados..... La capa oculta no es visible para el mundo exterior. Solo la capa de entrada y la capa de salida son visibles. Para todos los modelos DL, los datos deben ser de naturaleza numérica.
Paso 1: importar bibliotecas de claves
import numpy as np from keras.models import Sequential from keras.layers import Dense from keras.utils import np_utils
Paso 2: remodelar los datos
Cada imagen tiene un tamaño de 28X28, por lo que hay 784 píxeles. Entonces, la capa de salida tiene 10 salidas, la capa oculta tiene 784 neuronas y la capa de entrada tiene 784 entradas. Luego, el conjunto de datos se convierte en un tipo de datos flotante.
number_pix=X_train.shape[1]*X_train.shape[2]
X_train=X_train.reshape(X_train.shape[0], number_pix).astype('float32')
X_test=X_test.reshape(X_test.shape[0], number_pix).astype('float32')
Paso 3: normaliza los datos
Los modelos NN generalmente requieren datos escalados. En este fragmento de código, los datos se normalizan de (0-255) a (0-1) y la variableEn estadística y matemáticas, una "variable" es un símbolo que representa un valor que puede cambiar o variar. Existen diferentes tipos de variables, como las cualitativas, que describen características no numéricas, y las cuantitativas, que representan cantidades numéricas. Las variables son fundamentales en experimentos y estudios, ya que permiten analizar relaciones y patrones entre diferentes elementos, facilitando la comprensión de fenómenos complejos.... de destino se codifica en un solo uso para su posterior análisis. La variable de destino tiene un total de 10 clases (0-9)
X_train=X_train/255 X_test=X_test/255 y_train= np_utils.to_categorical(y_train) y_test= np_utils.to_categorical(y_test) num_classes=y_train.shape[1] print(num_classes)
Producción:
10
Ahora, crearemos una función NN_model y compilaremos la misma
Paso 4: definir la función del modelo
def nn_model():
model=Sequential()
model.add(Dense(number_pix, input_dim=number_pix, activation='relu'))
mode.add(Dense(num_classes, activation='softmax'))
model.compile(loss="categorical_crossentropy", optimiser="Adam", metrics=['accuracy'])
return model
Hay dos capas, una es una capa oculta con la función de activación ReLuLa función de activación ReLU (Rectified Linear Unit) es ampliamente utilizada en redes neuronales debido a su simplicidad y eficacia. Se define como ( f(x) = max(0, x) ), lo que significa que produce una salida de cero para valores negativos y un incremento lineal para valores positivos. Su capacidad para mitigar el problema del desvanecimiento del gradiente la convierte en una opción preferida en arquitecturas profundas.... y la otra es la capa de salida que usa la función softmaxLa función softmax es una herramienta matemática utilizada en el campo del aprendizaje automático, especialmente en redes neuronales. Convierte un vector de valores en una distribución de probabilidad, asignando probabilidades a cada clase en problemas de clasificación múltiple. Su fórmula normaliza las salidas, asegurando que la suma de todas las probabilidades sea igual a uno, lo que permite interpretar los resultados de manera efectiva. Es fundamental en la optimización de....
Paso 5: ejecutar el modelo
model=nn_model()
model.fit(X_train, y_train, validation_data=(X_test,y_test),epochs=10, batch_size=200, verbose=2)
score= model.evaluate(X_test, y_test, verbose=0)
print('The error is: %.2f%%'%(100-score[1]*100))
Producción:
Epoch 1/10 300/300 - 11s - loss: 0.2778 - accuracy: 0.9216 - val_loss: 0.1397 - val_accuracy: 0.9604 Epoch 2/10 300/300 - 2s - loss: 0.1121 - accuracy: 0.9675 - val_loss: 0.0977 - val_accuracy: 0.9692 Epoch 3/10 300/300 - 2s - loss: 0.0726 - accuracy: 0.9790 - val_loss: 0.0750 - val_accuracy: 0.9778 Epoch 4/10 300/300 - 2s - loss: 0.0513 - accuracy: 0.9851 - val_loss: 0.0656 - val_accuracy: 0.9796 Epoch 5/10 300/300 - 2s - loss: 0.0376 - accuracy: 0.9892 - val_loss: 0.0717 - val_accuracy: 0.9773 Epoch 6/10 300/300 - 2s - loss: 0.0269 - accuracy: 0.9928 - val_loss: 0.0637 - val_accuracy: 0.9797 Epoch 7/10 300/300 - 2s - loss: 0.0208 - accuracy: 0.9948 - val_loss: 0.0600 - val_accuracy: 0.9824 Epoch 8/10 300/300 - 2s - loss: 0.0153 - accuracy: 0.9962 - val_loss: 0.0581 - val_accuracy: 0.9815 Epoch 9/10 300/300 - 2s - loss: 0.0111 - accuracy: 0.9976 - val_loss: 0.0631 - val_accuracy: 0.9807 Epoch 10/10 300/300 - 2s - loss: 0.0082 - accuracy: 0.9985 - val_loss: 0.0609 - val_accuracy: 0.9828 The error is: 1.72%
En los resultados del modelo, es visible a medida que aumenta el número de épocas, mejora la precisión. El error es del 1,72%, menor es el error, mayor es la precisión del modelo.
Modelo de red neuronal convolucional usando MNIST
En esta sección, crearemos modelos CNN simples para MNIST que demuestran capas convolucionales, capas de agrupación y capas de abandono.
Paso 1: importar todas las bibliotecas necesarias
import numpy as np from keras.models import Sequential from keras.layers import Dense from keras.utils import np_utils from keras.layers import Dropout from keras.layers import Flatten from keras.layers.convolutional import Conv2D from keras.layers.convolutional import MaxPooling2D
Paso 2: Configure la semilla para la reproducibilidad y cargue los datos MNIST data
seed=10 np.random.seed(seed) (X_train,y_train), (X_test, y_test)= mnist.load_data()
Paso 3: convierta los datos en valores flotantes
X_train=X_train.reshape(X_train.shape[0], 1,28,28).astype('float32')
X_test=X_test.reshape(X_test.shape[0], 1,28,28).astype('float32')
Paso 4: normaliza los datos
X_train=X_train/255 X_test=X_test/255 y_train= np_utils.to_categorical(y_train) y_test= np_utils.to_categorical(y_test) num_classes=y_train.shape[1] print(num_classes)
Una arquitectura clásica de CNN se ve como se muestra a continuación:
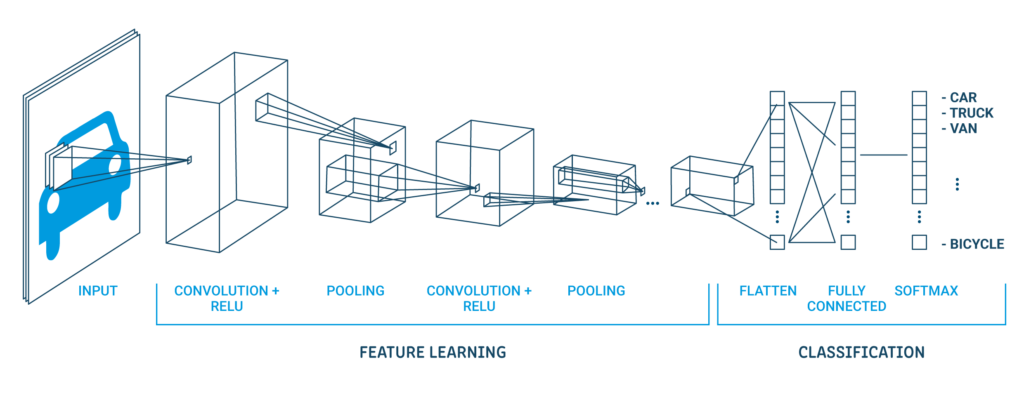
| Capa de salida (10 salidas) |
| Capa oculta (128 neuronas) |
| Capa plana |
| Capa de abandono 20% |
| Capa de agrupación máxima 2 × 2 |
| Capa convolucional 32 mapas, 5 × 5 |
| Capa visible 1x28x28 |
La primera capa oculta es una capa convolucional llamada Convolution2D. Dispone de 32 mapas de características con tamaño 5 × 5 y función rectificadora. Esta es la capa de entrada. La siguiente es la capa de agrupación que toma el valor máximo llamada MaxPooling2D. En este modelo, se configura como un tamaño de piscina de 2 × 2.
En la capa de abandono ocurre la regularizaciónLa regularización es un proceso administrativo que busca formalizar la situación de personas o entidades que operan fuera del marco legal. Este procedimiento es fundamental para garantizar derechos y deberes, así como para fomentar la inclusión social y económica. En muchos países, la regularización se aplica en contextos migratorios, laborales y fiscales, permitiendo a quienes se encuentran en situaciones irregulares acceder a beneficios y protegerse de posibles sanciones..... Está configurado para excluir aleatoriamente el 20% de las neuronas de la capa para evitar el sobreajuste. La quinta capa es la capa aplanada que convierte los datos de la matriz 2D en un vector llamado Aplanar. Permite que la salida sea procesada completamente por una capa estándar completamente conectada.
A continuación, se utiliza la capa completamente conectada con 128 neuronas y la función de activaciónLa función de activación es un componente clave en las redes neuronales, ya que determina la salida de una neurona en función de su entrada. Su propósito principal es introducir no linealidades en el modelo, permitiendo que aprenda patrones complejos en los datos. Existen diversas funciones de activación, como la sigmoide, ReLU y tanh, cada una con características particulares que afectan el rendimiento del modelo en diferentes aplicaciones.... del rectificador. Finalmente, la capa de salida tiene 10 neuronas para las 10 clases y una función de activación softmax para generar predicciones similares a la probabilidad para cada clase.
Paso 5: ejecutar el modelo
def cnn_model():
model=Sequential()
model.add(Conv2D(32,5,5, padding='same',input_shape=(1,28,28), activation='relu'))
model.add(MaxPooling2D(pool_size=(2,2), padding='same'))
model.add(Dropout(0.2))
model.add(Flatten())
model.add(Dense(128, activation='relu'))
model.add(Dense(num_classes, activation='softmax'))
model.compile(loss="categorical_crossentropy", optimizer="adam", metrics=['accuracy'])
return model
model=cnn_model()
model.fit(X_train, y_train, validation_data=(X_test,y_test),epochs=10, batch_size=200, verbose=2)
score= model.evaluate(X_test, y_test, verbose=0)
print('The error is: %.2f%%'%(100-score[1]*100))
Producción:
Epoch 1/10 300/300 - 2s - loss: 0.7825 - accuracy: 0.7637 - val_loss: 0.3071 - val_accuracy: 0.9069 Epoch 2/10 300/300 - 1s - loss: 0.3505 - accuracy: 0.8908 - val_loss: 0.2192 - val_accuracy: 0.9336 Epoch 3/10 300/300 - 1s - loss: 0.2768 - accuracy: 0.9126 - val_loss: 0.1771 - val_accuracy: 0.9426 Epoch 4/10 300/300 - 1s - loss: 0.2392 - accuracy: 0.9251 - val_loss: 0.1508 - val_accuracy: 0.9537 Epoch 5/10 300/300 - 1s - loss: 0.2164 - accuracy: 0.9325 - val_loss: 0.1423 - val_accuracy: 0.9546 Epoch 6/10 300/300 - 1s - loss: 0.1997 - accuracy: 0.9380 - val_loss: 0.1279 - val_accuracy: 0.9607 Epoch 7/10 300/300 - 1s - loss: 0.1856 - accuracy: 0.9415 - val_loss: 0.1179 - val_accuracy: 0.9632 Epoch 8/10 300/300 - 1s - loss: 0.1777 - accuracy: 0.9433 - val_loss: 0.1119 - val_accuracy: 0.9642 Epoch 9/10 300/300 - 1s - loss: 0.1689 - accuracy: 0.9469 - val_loss: 0.1093 - val_accuracy: 0.9667 Epoch 10/10 300/300 - 1s - loss: 0.1605 - accuracy: 0.9493 - val_loss: 0.1053 - val_accuracy: 0.9659 The error is: 3.41%
En los resultados del modelo, es visible a medida que aumenta el número de épocas, mejora la precisión. El error es 3.41%, menor error mayor precisión del modelo.
Espero que haya disfrutado de la lectura y no dude en usar mi código para probarlo para sus propósitos. Además, si hay algún comentario sobre el código o solo la publicación del blog, no dude en comunicarse conmigo en [email protected]
Los medios que se muestran en este artículo sobre el procesamiento de imágenes mediante CNN no son propiedad de DataPeaker y se utilizan a discreción del autor.
Relacionado
Posts Relacionados:
- Clasificación de imágenes de CNN | Clasificación de imágenes mediante CNN
- Aplicaciones de procesamiento de imágenes digitales | Procesamiento de imágenes en Python
- Procesamiento de imágenes OpenCV | Procesamiento de imágenes con OpenCV
- Clasificación de imágenes mediante CNN: implementación de Python






