Prueba de hipótesis | Pruebas paramétricas y no paramétricas

Este artículo fue publicado como parte del Blogatón de ciencia de datos

Introducción

La prueba de hipótesis es uno de los conceptos más importantes en Estadística que es muy utilizado por Estadísticos, Ingenieros de aprendizaje automático, y Científicos de datos.

En la prueba de hipótesis, las pruebas estadísticas se utilizan para comprobar si el hipótesis nulaLa hipótesis nula es un concepto fundamental en la estadística que establece una afirmación inicial sobre un parámetro poblacional. Su propósito es ser probada y, en caso de ser refutada, permite aceptar la hipótesis alternativa. Este enfoque es esencial en la investigación científica, ya que proporciona un marco para evaluar la evidencia empírica y tomar decisiones basadas en datos. Su formulación y análisis son cruciales en estudios estadísticos.... es rechazado o no rechazado. Estas Pruebas estadísticas asumir un nulo hipótesis de ninguna relación o ninguna diferencia entre los grupos.

Entonces, en este artículo, discutiremos la prueba estadística para la prueba de hipótesis, incluidas las pruebas paramétricas y no paramétricas.

Tabla de contenido

1. ¿Qué son las pruebas paramétricas?

2. ¿Qué son las pruebas no paramétricas?

3. Pruebas paramétricas para pruebas de hipótesis

• Prueba t
• Prueba Z
• Prueba F
• ANOVA

4. Pruebas no paramétricas para pruebas de hipótesis

• Chi-cuadrado
• Prueba U de Mann-Whitney
• Prueba H de Kruskal-Wallis

Empecemos,

Pruebas paramétricas

El principio básico detrás de las pruebas paramétricas es que tenemos un conjunto fijo de parámetrosLos "parámetros" son variables o criterios que se utilizan para definir, medir o evaluar un fenómeno o sistema. En diversos campos como la estadística, la informática y la investigación científica, los parámetros son fundamentales para establecer normas y estándares que guían el análisis y la interpretación de datos. Su adecuada selección y manejo son cruciales para obtener resultados precisos y relevantes en cualquier estudio o proyecto.... que se utilizan para determinar un modelo probabilístico que también se puede utilizar en Machine Learning.

Las pruebas paramétricas son aquellas pruebas para las que tenemos un conocimiento previo de la distribución de la población (es decir, normal), o si no es así, podemos aproximarla fácilmente a una distribución normal, lo cual es posible con la ayuda del Teorema del límite central.

Los parámetros para usar la distribución normal son:

Finalmente, la clasificación de una prueba como paramétrica depende completamente de los supuestos de la población. Hay muchas pruebas paramétricas disponibles, algunas de las cuales son las siguientes:

• Para encontrar el intervalo de confianza para las medias poblacionales con la ayuda de la desviación estándar conocida.
• Determinar el intervalo de confianza para las medias poblacionales junto con la desviación estándar desconocida.
• Encontrar el intervalo de confianza para la varianza de la población.
• Encontrar el intervalo de confianza para la diferencia de dos medias, con un valor de desviación estándar desconocido.

Pruebas no paramétricas

En las pruebas no paramétricas, no hacemos ninguna suposición sobre los parámetros para la población dada o la población que estamos estudiando. De hecho, estas pruebas no dependen de la población.
Por lo tanto, no hay un conjunto fijo de parámetros disponible, y tampoco hay distribución (distribución normal, etc.) de ningún tipo disponible para su uso.

Esta es también la razón por la que las pruebas no paramétricas también se denominan pruebas sin distribución.
En la actualidad, las pruebas no paramétricas están ganando popularidad y un impacto de influencia, algunas de las razones detrás de esta fama es:

• La razón principal es que no hay necesidad de ser educado al usar pruebas paramétricas.
• La segunda razón es que no necesitamos hacer suposiciones sobre la población dada (o tomada) sobre la cual estamos haciendo el análisis.
• La mayoría de las pruebas no paramétricas disponibles son muy fáciles de aplicar y comprender también, es decir, la complejidad es muy baja.

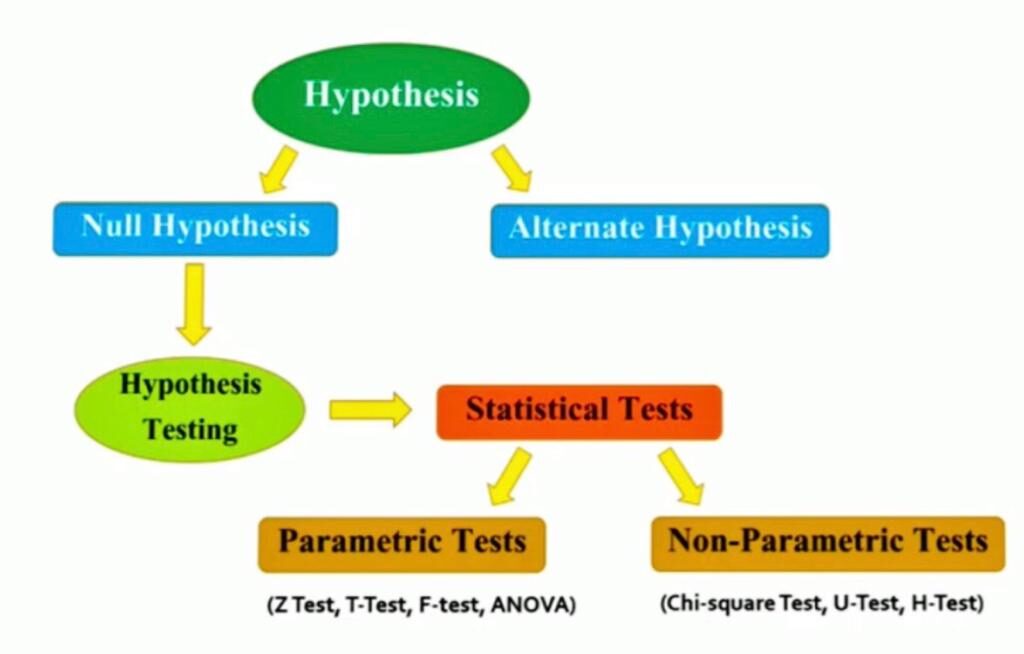
Fuente de la imagen: imágenes de Google

Prueba T

1. Es una prueba paramétrica de prueba de hipótesis basada en Distribución T de Student.

2. Esencialmente, se trata de probar la significancia de la diferencia de los valores medios cuando el tamaño de la muestra es pequeño (es decir, menos de 30) y cuando la desviación estándar de la población no está disponible.

3. Supuestos de esta prueba:

• La distribución de la población es normal y
• Las muestras son aleatorias e independientes.
• El tamaño de la muestra es pequeño.
• Se desconoce la desviación estándar de la población.

4. La prueba ‘U’ de Mann-Whitney es una contraparte no paramétrica de la prueba T.

Una prueba T puede ser:

Prueba T de una muestra: Comparar una media muestral con la media poblacional.

dónde,

X es la media muestral

s es la desviación estándar de la muestra

norte es el tamaño de la muestra

μ es la media de la población

Prueba T de dos muestras: Comparar las medias de dos muestras diferentes.

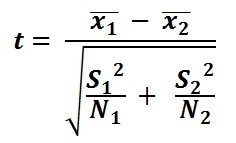
dónde,

X₁ es la media muestral del primer grupo

X₂ es la media muestral del segundo grupo

S₁ es la desviación estándar de la muestra 1

S₂ es la desviación estándar de la muestra 2

norte es el tamaño de la muestra

Conclusión:

• Si el valor de la estadística de prueba es mayor que el valor de la tabla -> Rechaza la hipótesis nula.
• Si el valor de la estadística de prueba es menor que el valor de la tabla -> No rechaces la hipótesis nula.

Prueba Z

1. Es una prueba paramétrica de prueba de hipótesis.

2. Se utiliza para determinar si las medias son diferentes cuando se conoce la varianza de la población y el tamaño de la muestra es grande (es decir, mayor de 30).

3. Supuestos de esta prueba:

• La distribución de la población es normal
• Las muestras son aleatorias e independientes.
• El tamaño de la muestra es grande.
• Se conoce la desviación estándar de la población.

Una prueba Z puede ser:

Prueba Z de una muestra: Comparar una media muestral con la media poblacional.

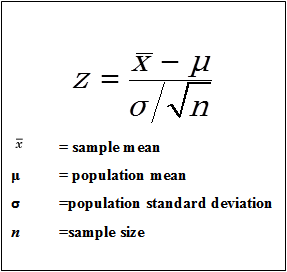
Fuente de la imagen: imágenes de Google

Prueba Z de dos muestras: Comparar las medias de dos muestras diferentes.

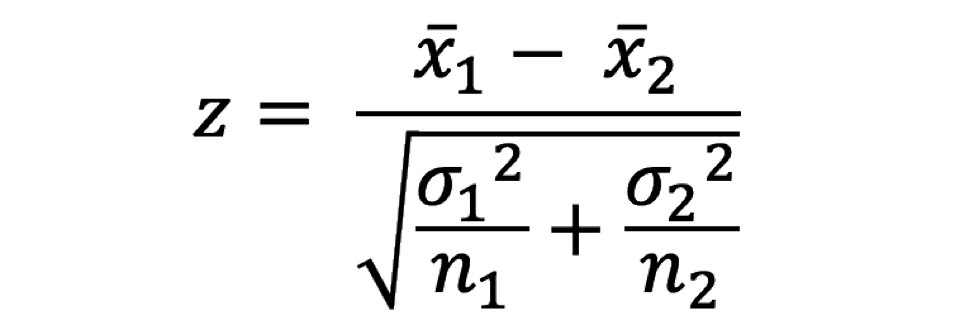
dónde,

X₁ es la media muestral del primer grupo

X₂ es la media muestral del segundo grupo

σ₁ es la desviación estándar de la población 1

σ₂ es la desviación estándar de la población 2

norte es el tamaño de la muestra

Prueba F

1. Es una prueba paramétrica de prueba de hipótesis basada en Distribución F de Snedecor.

2. Es una prueba para la hipótesis nula de que dos poblaciones normales tienen la misma varianza.

3. Una prueba F se considera una comparación de la igualdad de las varianzas muestrales.

4. El estadístico F es simplemente una relación de dos varianzas.

5. Se calcula como:

F = s₁²/s₂²

6. Al cambiar la varianza en la relación, la prueba F se ha convertido en una prueba muy flexible. Luego se puede utilizar para:

• Pruebe la significancia general para un modelo de regresión.
• Comparar los ajustes de diferentes modelos y
• Probar la igualdad de medios.

7. Supuestos de esta prueba:

• La distribución de la población es normal y
• Las muestras se extraen de forma aleatoria e independiente.

ANOVA

1. También llamado como Análisis de variación, es una prueba paramétrica de prueba de hipótesis.

2. Es una extensión de la prueba T y la prueba Z.

3. Se utiliza para probar la significancia de las diferencias en los valores medios entre más de dos grupos de muestra.

4. Utiliza la prueba F para probar estadísticamente la igualdad de medias y la varianza relativa entre ellas.

5. Supuestos de esta prueba:

• La distribución de la población es normal y
• Las muestras son aleatorias e independientes.
• Homogeneidad de la varianza muestral.

6. ANOVA unidireccional y ANOVA bidireccional son tipos.

7. Estadístico F = varianza entre las medias de la muestra / varianza dentro de la muestra

Prueba de chi-cuadrado

1. Es una prueba no paramétrica de prueba de hipótesis.

2. Como prueba no paramétrica, se puede utilizar chi-cuadrado:

• prueba de bondad de ajuste.
• como prueba de independencia de dos variables.

3. Ayuda a evaluar la bondad del ajuste entre un conjunto de observados y esperados teóricamente.

4. Hace una comparación entre las frecuencias esperadas y las frecuencias observadas.

5. Cuanto mayor sea la diferencia, mayor será el valor de chi-cuadrado.

6. Si no hay diferencia entre las frecuencias esperadas y observadas, entonces el valor de chi-cuadrado es igual a cero.

7. También se conoce como el «Prueba de bondad de ajuste» que determina si una distribución particular se ajusta a los datos observados o no.

8. Se calcula como:

9. Chi-cuadrado también se usa para probar la independencia de dos variables.

10. Condiciones para la prueba de chi-cuadrado:

• Recopile y registre las observaciones al azar.
• En la muestra, todas las entidades deben ser independientes.
• Ninguno de los grupos debe contener muy pocos elementos, digamos menos de 10.
• El número total razonablemente grande de artículos. Normalmente, debería ser al menos 50, por pequeño que sea el número de grupos.

11. Chi-cuadrado como prueba paramétrica se utiliza como prueba para la varianza de la población basada en la varianza de la muestra.

12. Si tomamos cada una de una colección de varianzas muestrales, las dividimos por la varianza poblacional conocida y multiplicamos estos cocientes por (n-1), donde n significa el número de elementos en la muestra, obtenemos los valores de chi-cuadrado.

13. Se calcula como:

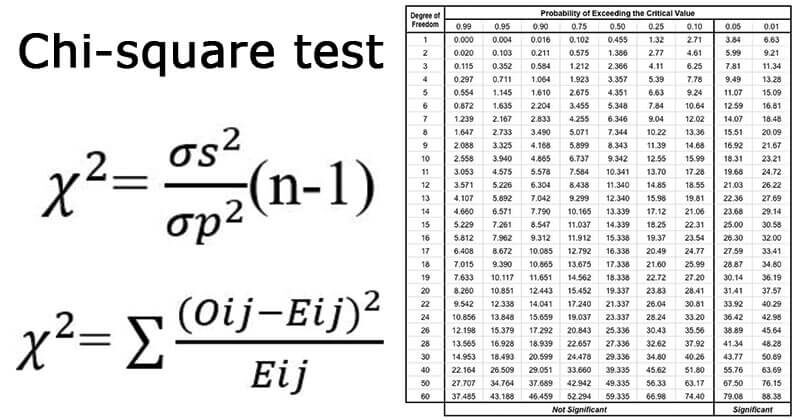
Prueba U de Mann-Whitney

1. Es una prueba no paramétrica de prueba de hipótesis.

2. Esta prueba se utiliza para investigar si se seleccionaron dos muestras independientes de una población que tiene la misma distribución.

3. Es una verdadera contraparte no paramétrica de la prueba T y proporciona las estimaciones de significancia más precisas, especialmente cuando los tamaños de muestra son pequeños y la población no tiene una distribución normal.

4. Se basa en la comparación de cada observación de la primera muestra con cada observación de la otra muestra.

5. La estadística de prueba utilizada aquí es «U».

6. El valor máximo de «U» es ‘n₁*norte₂‘y el valor mínimo es cero.

7. También se conoce como:

• Prueba de Mann-Whitney Wilcoxon.
• Prueba de rango de Mann-Whitney Wilcoxon.

8. Matemáticamente, U viene dada por:

U₁ = R₁ – n₁(norte₁+1) / 2

donde n₁ es el tamaño de la muestra para la muestra 1, y R₁ es la suma de rangos en la Muestra 1.

U₂ = R₂ – n₂(norte₂+1) / 2

Al consultar las tablas de significancia, los valores menores de U₁ y tú₂ son usados. La suma de dos valores viene dada por,

U₁ + U₂ = {R₁ – n₁(norte₁+1) / 2} + {R₂ – n₂(norte₂+1) / 2}

Sabiendo que R₁+ R₂ = N (N + 1) / 2 y N = n₁+ n₂, y haciendo algo de álgebra, encontramos que la suma es:

U₁ + U₂ = n₁*norte₂

Prueba H de Kruskal-Wallis

1. Es una prueba no paramétrica de prueba de hipótesis.

2. Esta prueba se utiliza para comparar dos o más muestras independientes de tamaños de muestra iguales o diferentes.

3. Extiende la prueba U de Mann-Whitney, que se utiliza para comparar solo dos grupos.

4. El ANOVA de una vía es el equivalente paramétrico de esta prueba. Y es por eso que también se conoce como ‘ANOVA unidireccional en rangos.

5. Utiliza rangos en lugar de datos reales.

6. No asume que la población esté distribuida normalmente.

7. La estadística de prueba utilizada aquí es «H».

¡Esto completa la discusión de hoy!

Notas finales

¡Gracias por leer!

Espero que haya disfrutado del artículo y haya aumentado sus conocimientos sobre las pruebas estadísticas para la prueba de hipótesis en estadística.

Por favor no dude en ponerse en contacto conmigo sobre Correo electrónico

¿Algo no mencionado o quieres compartir tus pensamientos? No dude en comentar a continuación y me pondré en contacto con usted.

Para los artículos restantes, consulte el Enlace.

Sobre el Autor

Aashi Goyal

Actualmente, estoy cursando mi Licenciatura en Tecnología (B.Tech) en Ingeniería Electrónica y de Comunicación de Universidad Guru Jambheshwar (GJU), Hisar. Estoy muy entusiasmado con la estadística, el aprendizaje automático y el aprendizaje profundoEl aprendizaje profundo, una subdisciplina de la inteligencia artificial, se basa en redes neuronales artificiales para analizar y procesar grandes volúmenes de datos. Esta técnica permite a las máquinas aprender patrones y realizar tareas complejas, como el reconocimiento de voz y la visión por computadora. Su capacidad para mejorar continuamente a medida que se le proporcionan más datos la convierte en una herramienta clave en diversas industrias, desde la salud....

Los medios que se muestran en este artículo no son propiedad de DataPeaker y se utilizan a discreción del autor.

Relacionado