Visión general
- La asimetría es un concepto estadístico clave que debe conocer en los campos de la ciencia de datos y el análisis.
- Aprenda qué es la asimetría y por qué es importante para usted como profesional de la ciencia de datos
Introducción
El concepto de asimetría está integrado en nuestra forma de pensar. Cuando miramos una visualización, nuestra mente discierne intuitivamente el patrón en ese gráfico.
Como ya sabrá, India tiene más del 50% de su población menor de 25 años y más del 65% menor de 35 años. Si traza la distribución de la edad de la población de India, encontrará que hay una joroba en el lado izquierdo de distribución y el lado derecho es comparativamente plano. En otras palabras, podemos decir que hay un sesgo hacia el final, ¿verdad?
Entonces, incluso si no ha leído sobre la asimetría como profesional de la ciencia de datos o el análisis, definitivamente ha interactuado con el concepto en una nota informal. Y en realidad es un tema bastante fácil en estadística y, sin embargo, mucha gente lo lee en su prisa por aprender otros conceptos de ciencia de datos aparentemente complejos. Para mí, eso es un error.
La asimetría es un concepto estadístico fundamental que todo el mundo en ciencia de datos y análisis debe conocer. Es algo de lo que simplemente no podemos huir. Y estoy seguro de que lo entenderá al final de este artículo.
Aquí, discutiremos el concepto de asimetría de la manera más fácil posible. Aprenderá sobre la asimetría, sus tipos y su importancia en el campo de la ciencia de datos. Así que abróchese el cinturón porque aprenderá un concepto que valorará durante toda su carrera en ciencia de datos.
Nota: Aquí hay un par de recursos que lo ayudarán a profundizar en el mundo de las estadísticas para la ciencia de datos:
Tabla de contenido
- ¿Qué es la asimetría?
- ¿Por qué es importante la asimetría?
- ¿Qué es una distribución normal?
- Comprensión de la distribución sesgada positivamente
- Comprensión de la distribución sesgada negativamente
¿Qué es la asimetría?
La asimetría es la medida de la asimetría de una distribución de probabilidad idealmente simétrica y viene dada por la tercer momento estandarizado. Si eso suena demasiado complejo, ¡no se preocupe! Déjeme desglosarlo por usted.
En palabras simples, la asimetría es la medida de cuánto se desvía la distribución de probabilidad de una variable aleatoria de la distribución normal. Ahora, podría estar pensando: ¿por qué estoy hablando de distribución normal aquí?
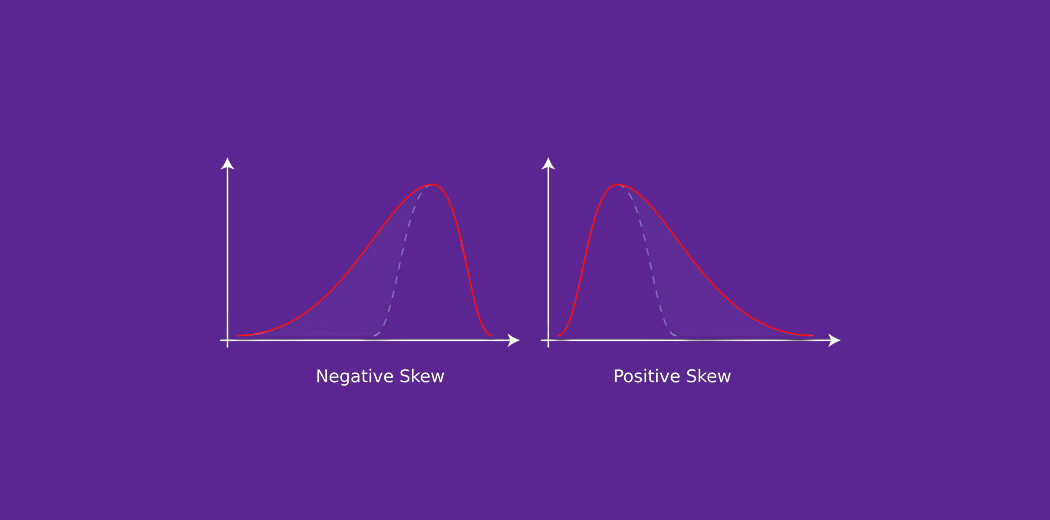
Bueno, la distribución normal es la distribución de probabilidad sin ningún sesgo. Puede ver la imagen a continuación que muestra una distribución simétrica que es básicamente una distribución normal y puede ver que es simétrica en ambos lados de la línea discontinua. Aparte de esto, hay dos tipos de asimetría:
- Sesgo positivo
- Asimetría negativa
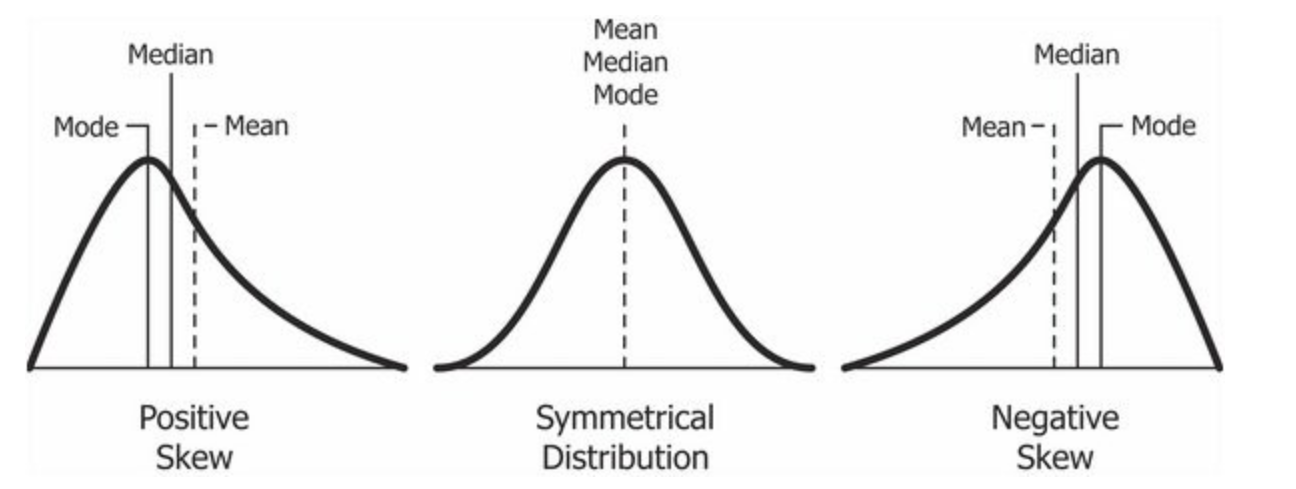
Créditos: Wikipedia
La distribución de probabilidad con su cola en el lado derecho es una distribución sesgada positivamente y la que tiene su cola en el lado izquierdo es una distribución sesgada negativamente. Si encuentra confusas las cifras anteriores, está bien. Comprenderemos esto con más detalle más adelante.
Antes de eso, entendamos por qué la asimetría es un concepto tan importante para usted como profesional de la ciencia de datos.
¿Por qué es importante la asimetría?
Ahora, sabemos que la asimetría es la medida de la asimetría y sus tipos se distinguen por el lado en el que se encuentra la cola de la distribución de probabilidad. Pero, ¿por qué es importante conocer la asimetría de los datos?
Primero, los modelos lineales funcionan bajo el supuesto de que la distribución de la variable independiente y la variable objetivo son similares. Por lo tanto, conocer la asimetría de los datos nos ayuda a crear mejores modelos lineales.
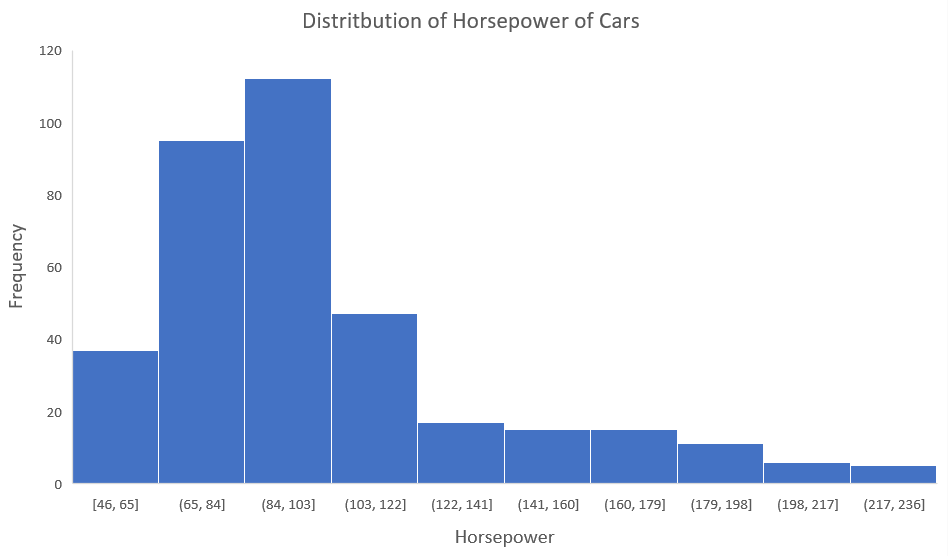
En segundo lugar, echemos un vistazo a la siguiente distribución. Es la distribución de caballos de fuerza de los automóviles:
Puede ver claramente que la distribución anterior está sesgada positivamente. Ahora, digamos que desea usar esto como una función para el modelo que predecirá las millas por galón (millas por galón) de un automóvil.
Dado que nuestros datos están sesgados positivamente aquí, significa que tiene un mayor número de puntos de datos con valores bajos, es decir, automóviles con menos caballos de fuerza. Entonces, cuando entrenamos nuestro modelo con estos datos, se desempeñará mejor en la predicción de las millas por galón de los autos con menor potencia en comparación con aquellos con mayor potencia.
Además, la asimetría nos dice sobre la dirección de valores atípicos. Puede ver que nuestra distribución está sesgada positivamente y la mayoría de los valores atípicos están presentes en el lado derecho de la distribución.
Nota: La asimetría no nos dice sobre el número de valores atípicos. Solo nos dice la dirección.
Ahora que sabemos por qué la asimetría es importante, entendamos las distribuciones que les mostré anteriormente.
¿Qué es la distribución simétrica / normal?
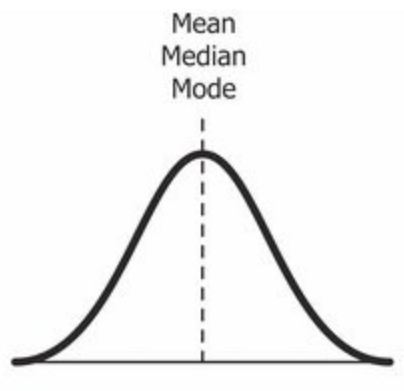
Créditos: Wikipedia
Sí, volvemos de nuevo con la distribución normal. Se utiliza como referencia para determinar la asimetría de una distribución. Como mencioné anteriormente, la distribución normal ideal es la distribución de probabilidad casi sin asimetría. Es casi perfectamente simétrico. Debido a esto, el valor de asimetría para una distribución normal es cero.
Pero, ¿por qué es casi perfectamente simétrico y no absolutamente simétrico?
Eso es porque, en realidad, ningún dato de palabras reales tiene una distribución perfectamente normal. Por lo tanto, incluso el valor de la asimetría no es exactamente cero; es casi cero. Aunque el valor de cero se utiliza como referencia para determinar la asimetría de una distribución.
Puede ver en la imagen de arriba que la misma línea representa la media, la mediana y la moda. Es porque la media, la mediana y la moda de una distribución perfectamente normal son iguales.
Hasta ahora, hemos entendido la asimetría de la distribución normal usando una distribución de probabilidad o frecuencia. Ahora, entendamos esto en términos de un diagrama de caja porque esa es la forma más común de ver una distribución en el espacio de la ciencia de datos.
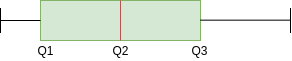
La imagen de arriba es una gráfica de caja de distribución simétrica. Notará aquí que la distancia entre Q1 y Q2 y Q2 y Q3 es igual, es decir:
Pero eso no es suficiente para concluir si una distribución está sesgada o no. También echamos un vistazo a la longitud del bigote; si son iguales, entonces podemos decir que la distribución es simétrica, es decir, no está sesgada.
Ahora que hemos discutido la asimetría en la distribución normal, es hora de aprender sobre los dos tipos de asimetría que discutimos anteriormente. Comencemos con la asimetría positiva.
Comprensión de la distribución sesgada positivamente
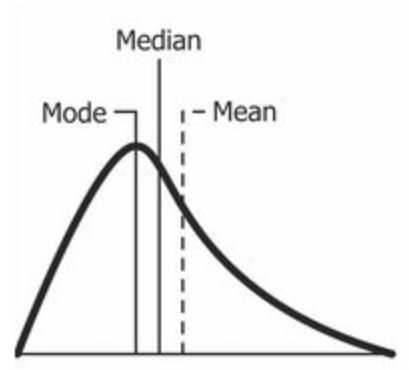
Fuente: Wikipedia
Una distribución sesgada positivamente es la distribución con la cola en su lado derecho. El valor de la asimetría para una distribución sesgada positivamente es mayor que cero. Como ya habrá entendido al mirar la figura, el valor de la media es el mayor, seguido de la mediana y luego de la moda.
Entonces, ¿por qué está pasando esto?
Bueno, la respuesta a eso es que la asimetría de la distribución está a la derecha; hace que la media sea mayor que la medianaLa mediana es una medida estadística que representa el valor central de un conjunto de datos ordenados. Para calcularla, se organizan los datos de menor a mayor y se identifica el número que se encuentra en el medio. Si hay un número par de observaciones, se promedia los dos valores centrales. Este indicador es especialmente útil en distribuciones asimétricas, ya que no se ve afectado por valores extremos.... y eventualmente se mueva hacia la derecha. Además, la moda ocurre en la frecuencia más alta de la distribución que está en el lado izquierdo de la mediana. Por lo tanto, moda <mediana <media.
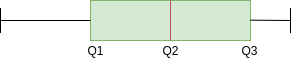
En el diagrama de caja anterior, puede ver que Q2 está presente más cerca de Q1. Esto representa una distribución sesgada positivamente. En términos de cuartiles, puede estar dado por:
En este caso, fue muy fácil saber si los datos están sesgados o no. Pero, ¿y si tenemos algo como esto?
Aquí, Q2-Q1 y Q3-Q2 son iguales y, sin embargo, la distribución está sesgada positivamente. Los más atentos habrán notado que la longitud del bigote derecho es mayor que el izquierdo. De esto, podemos concluir que los datos están sesgados positivamente.
Entonces, el primer paso es siempre verificar la igualdad de Q2-Q1 y Q3-Q2. Si se encuentra igual, buscamos la longitud de los bigotes.
Comprensión de la distribución sesgada negativamente
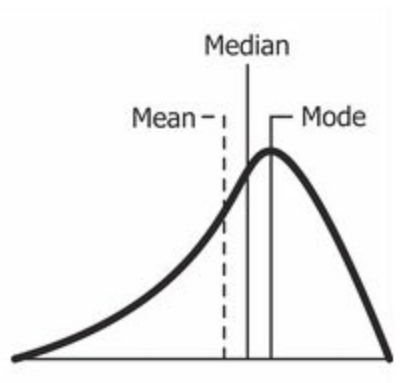
Fuente: Wikipedia
Como ya habrá adivinado, una distribución sesgada negativamente es la distribución con la cola en su lado izquierdo. El valor de la asimetría para una distribución sesgada negativamente es menor que cero. También puede ver en la figura"Figura" es un término que se utiliza en diversos contextos, desde el arte hasta la anatomía. En el ámbito artístico, se refiere a la representación de formas humanas o animales en esculturas y pinturas. En la anatomía, designa la forma y estructura del cuerpo. Además, en matemáticas, "figura" se relaciona con las formas geométricas. Su versatilidad hace que sea un concepto fundamental en múltiples disciplinas.... anterior que el media <mediana <moda.
En la gráfica de caja, la relación entre los cuartiles para una asimetría negativa viene dada por:
Similar a lo que hicimos antes, si Q3-Q2 y Q2-Q1 son iguales, entonces buscamos la longitud de los bigotes. Y si la longitud del bigote izquierdo es mayor que la del derecho, entonces podemos decir que los datos están sesgados negativamente.
¿Cómo transformamos los datos sesgados?
Dado que sabe cuánto pueden afectar los datos asimétricos a las capacidades de predicción de nuestro modelo de aprendizaje automático, es mejor transformar los datos asimétricos en datos distribuidos normalmente. Estas son algunas de las formas en que puede transformar sus datos sesgados:
- Transformación de poder
- Transformación de registros
- Transformación exponencial
Nota: La selección de la transformación depende de las características estadísticas de los datos.
Notas finales
En este artículo, cubrimos el concepto de asimetría, sus tipos y por qué es importante en el campo de la ciencia de datos. Hablamos de la asimetría a nivel conceptual, pero si desea profundizar, puede explorar su parte matemática como paso siguiente.
Además, puede leer artículos sobre otros temas importantes de estadística:
Conéctese conmigo en la sección de comentarios a continuación si tiene alguna pregunta.
