Regresión lineal | Introducción a la regresión lineal para la ciencia de datos

Este artículo fue publicado como parte del Blogatón de ciencia de datos

Introducción

Si está leyendo este artículo, supongo que ya está en el mundo de la ciencia de datos y tiene una idea sobre el aprendizaje automático. Si no es así, no hay problema. Comenzaré con las terminologías básicas que es necesario conocer antes de comprender el tema principal de discusión, es decir, regresión lineal.

Este artículo cubrirá todo lo que necesita saber sobre la regresión lineal, el primer algoritmo de aprendizaje automático de la ciencia de datos.

Tabla de contenidos

1. Breve introducción al aprendizaje automático y sus tipos
2. Comprensión de la regresión lineal
3. Supuestos de regresión lineal.
4. Cómo lidiar con la violación de los supuestos
5. Métricas de evaluación para problemas de regresión

Introducción al aprendizaje automático

El aprendizaje automático es una rama de la inteligencia artificial (IA) centrada en la creación de aplicaciones que aprenden de los datos y mejoran su precisión con el tiempo sin estar programadas para hacerlo.

Tipos de aprendizaje automático:

Aprendizaje automático supervisado: Es una técnica de ML en la que los modelos se entrenan con datos etiquetados, es decir, se proporciona una variableEn estadística y matemáticas, una "variable" es un símbolo que representa un valor que puede cambiar o variar. Existen diferentes tipos de variables, como las cualitativas, que describen características no numéricas, y las cuantitativas, que representan cantidades numéricas. Las variables son fundamentales en experimentos y estudios, ya que permiten analizar relaciones y patrones entre diferentes elementos, facilitando la comprensión de fenómenos complejos.... de salida en este tipo de problemas. Aquí, los modelos encuentran la función de mapeo para mapear las variables de entrada con la variable de salida o las etiquetas.
Regresión y clasificación Los problemas son parte del aprendizaje automático supervisado.

Aprendizaje automático no supervisado: Es la técnica en la que los modelos no reciben los datos etiquetados y tienen que encontrar los patrones y la estructura en los datos para conocer los datos.
Agrupación y asociación Los algoritmos son parte del AA no supervisado.

Comprensión de la regresión lineal

En las palabras más simples Regresión lineal es el modelo de aprendizaje automático supervisado en el que el modelo encuentra la línea lineal de mejor ajuste entre la variable independiente y dependiente es decir, encuentra la relación lineal entre la variable dependiente y la independiente.

La regresión lineal es de dos tipos: Simple y múltiple. Regresión lineal simple es donde solo está presente una variable independiente y el modelo tiene que encontrar su relación lineal con la variable dependiente

Mientras en Regresión lineal múltiple hay más de una variable independiente para que el modelo encuentre la relación.

Ecuación de regresión lineal simple, donde b_o es la intersección, b₁ es coeficiente o pendiente, x es la variable independiente e y es la variable dependiente.

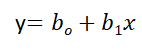
Ecuación de regresión lineal múltiple, donde bo es la intersección, b₁,B₂,B₃,B₄…,B_norte son coeficientes o pendientes de las variables independientes x₁,X₂,X₃,X₄…,X_norte e y es la variable dependiente.

El objetivo principal de un modelo de regresión lineal es encontrar la línea lineal que mejor se ajuste y los valores óptimos de intersección y coeficientes de manera que se minimice el error.
El error es la diferencia entre el valor real y el valor predicho y el objetivo es reducir esta diferencia.

Entendamos esto con la ayuda de un diagrama.

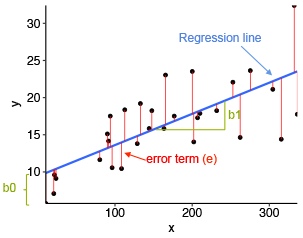
Fuente de imagen: herramientas estadísticas para análisis de datos de alto rendimiento

En el diagrama de arriba,

• x es nuestra variable dependiente que se traza en el eje x e y es la variable dependiente que se traza en el eje y.
• Los puntos negros son los puntos de datos, es decir, los valores reales.
• B_o es la intersección que es 10 y b₁ es la pendiente de la variable x.
• La línea azul es la línea de mejor ajuste predicha por el modelo, es decir, los valores predichos se encuentran en la línea azul.

La distancia vertical entre el punto de datos y la línea de regresión se conoce como error o residual. Cada punto de datos tiene un residuo y la suma de todas las diferencias se conoce como la suma de los residuos / errores.

Enfoque matemático:

Residual / Error = Valores reales – Valores predichos

Suma de residuos / errores = Suma (valores reales previstos)

Cuadrado de la suma de los residuos / errores = (Suma (valores reales previstos))²

es decir

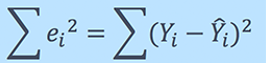
Para una comprensión profunda de las matemáticas detrás de la regresión lineal, consulte el adjunto explicación en video.

Supuestos de regresión lineal

Los supuestos básicos de la regresión lineal son los siguientes:

1. Linealidad: Establece que la variable dependiente Y debe estar relacionada linealmente con las variables independientes. Esta suposición se puede verificar trazando un diagrama de dispersión entre ambas variables.

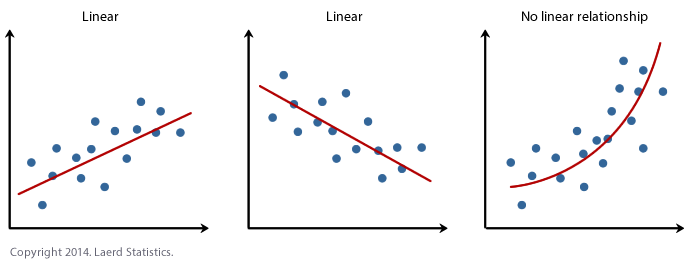
2. Normalidad: Las variables X e Y deben tener una distribución normal. Se pueden utilizar histogramas, gráficos de KDE y gráficos de QQ para comprobar el supuesto de normalidad.

Consulte mi blog adjunto para obtener una explicación detallada sobre cómo verificar la normalidad y transformar las variables que violan el supuesto.

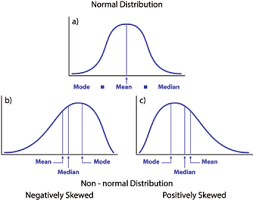
Fuente: https://heljves.com/gallery/vol_1_issue_1_2019_8.pdf

3. Homoscedasticidad: La varianza de los términos de error debe ser constante, es decir, la dispersión de los residuos debe ser constante para todos los valores de X. Este supuesto puede comprobarse trazando un gráfico de residuos. Si se viola la suposición, los puntos formarán una forma de embudo, de lo contrario serán constantes.

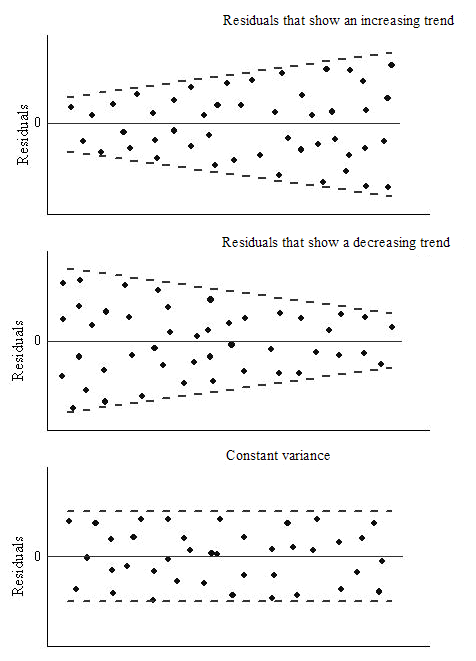
Fuente: OriginLab

4. Independencia / No multicolinealidad: Las variables deben ser independientes entre sí, es decir, no debe haber correlación entre las variables independientes. Para verificar el supuesto, podemos usar una matriz de correlación o una puntuación VIF. Si la puntuación de VIF es superior a 5, las variables están altamente correlacionadas.

En la imagen de abajo, existe una alta correlación entre las variables x5 y x6.

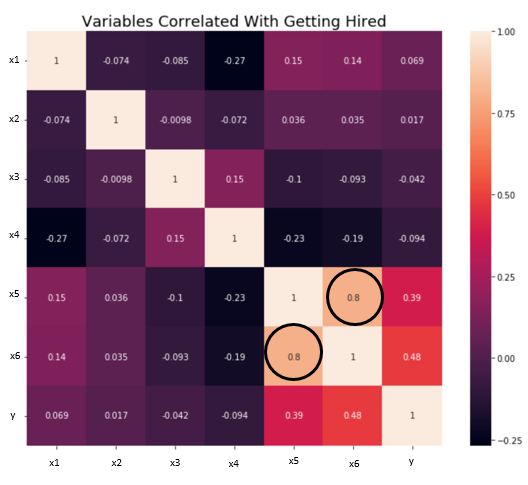
Fuente: hacia la ciencia de datos

5. los los términos de error deben distribuirse normalmente. Las gráficas QQ y los histogramas se pueden utilizar para comprobar la distribución de los términos de error.

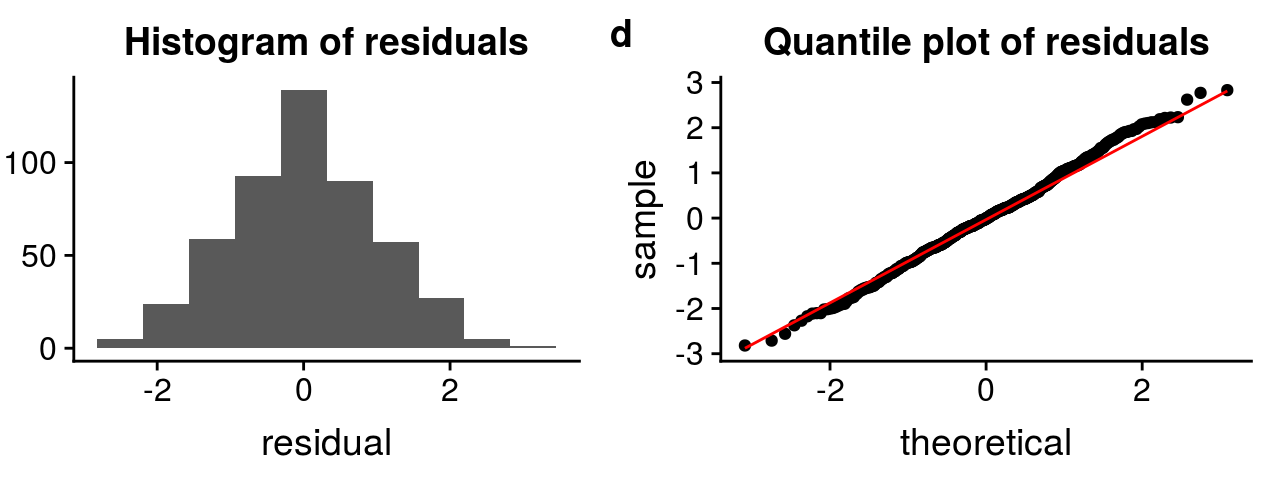
Fuente: http://rstudio-pubs-static.s3.amazonaws.com

6. Sin autocorrelación: Los términos de error deben ser independientes entre sí. La autocorrelación se puede probar mediante la prueba de Durbin Watson. La hipótesis nula asume que no existe autocorrelación. El valor de la prueba se encuentra entre 0 y 4. Si el valor de la prueba es 2, no hay autocorrelación.

Fuente: itfeature.com

Cómo lidiar con la violación de cualquiera de los supuestos

La violación de los supuestos conduce a una disminución en la precisión del modelo, por lo que las predicciones no son precisas y el error también es alto.
Por ejemplo, si se viola el supuesto de independencia, la relación entre la variable independiente y dependiente no se puede determinar con precisión.

Hay varios métodos y técnicas disponibles para hacer frente a la violación de los supuestos. Analicemos algunos de ellos a continuación.

Violación de la suposición de normalidad de variables o términos de error

Para tratar este problema, podemos transformar las variables a la distribución normal usando varias funciones de transformación como transformación logarítmica, Recíproca o Transformación Box-Cox.
Todas las funciones se discuten en este artículo mío: Cómo transformar en distribución normal

Violación del supuesto de multicolineraidad

Puede tratarse mediante:

• No hacer nada (si no hay una diferencia importante en la precisión)
• Eliminando algunas de las variables independientes altamente correlacionadas.
• Derivar una nueva característica combinando linealmente las variables independientes, como sumarlas o realizar alguna operación matemática.
• Realización de un análisis diseñado para variables altamente correlacionadas, como el análisis de componentes principales.

Métricas de evaluación para análisis de regresión

Para comprender el rendimiento del modelo de regresión, es necesario realizar una evaluación del modelo. Algunas de las métricas de evaluación utilizadas para el análisis de regresión son:

1. R cuadrado o coeficiente de determinación: La métrica más utilizada para la evaluación de modelos en el análisis de regresión es R cuadrado. Puede definirse como una relación de variación a la variación total. El valor de R al cuadrado se encuentra entre 0 y 1, cuanto más cerca de 1, mejor es el modelo.

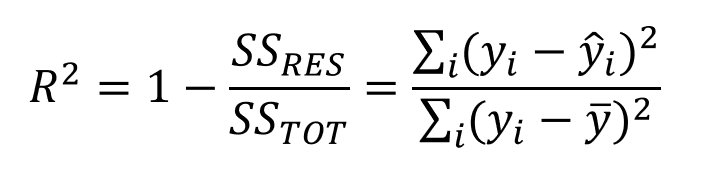
Fuente: medium.datadriveninvestor.com

donde SSRES es la suma residual de cuadrados y SSTOT es la suma total de cuadrados

2. R cuadrado ajustado: Es la mejora de R al cuadrado. El problema / inconveniente de R2 es que a medidaLa "medida" es un concepto fundamental en diversas disciplinas, que se refiere al proceso de cuantificar características o magnitudes de objetos, fenómenos o situaciones. En matemáticas, se utiliza para determinar longitudes, áreas y volúmenes, mientras que en ciencias sociales puede referirse a la evaluación de variables cualitativas y cuantitativas. La precisión en la medición es crucial para obtener resultados confiables y válidos en cualquier investigación o aplicación práctica.... que aumentan las características, el valor de R2 también aumenta, lo que da la ilusión de un buen modelo. Entonces, R2 ajustado resuelve el inconveniente de R2. Solo considera las características que son importantes para el modelo y muestra la mejora real del modelo.
R2 ajustado siempre es menor que R2.

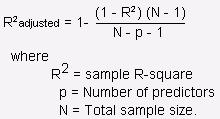
Fuente: stats.stackexchange.com

3. Error cuadrático medio (MSE): Otra métrica común para la evaluación es el error cuadrático medio, que es la media de la diferencia cuadrática de los valores reales frente a los predichos.

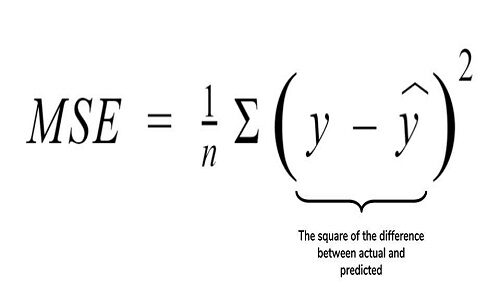
Fuente: cppsecrets.com

4. Error cuadrático medio (RMSE): Es la raíz de MSE, es decir, la raíz de la diferencia media de los valores reales y pronosticados. RMSE penaliza los grandes errores, mientras que MSE no lo hace.

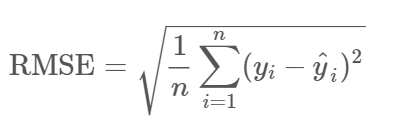
Fuente: community.qlik.com

Notas finales

Hemos cubierto la mayoría de los conceptos del modelo de regresión en este blog. Si desea explorar más sobre las matemáticas detrás del modelo, consulte los enlaces adjuntos al blog.

Por favor, siéntete libre de conectarte conmigo en LinkedIn y comparta sus valiosos aportes. Por favor, consulte mis otros artículos aquí.

Sobre el Autor :

Soy Deepanshi Dhingra, actualmente trabajo como investigador de ciencia de datos y poseo conocimientos de análisis, análisis de datos exploratorios, aprendizaje automático y aprendizaje profundoEl aprendizaje profundo, una subdisciplina de la inteligencia artificial, se basa en redes neuronales artificiales para analizar y procesar grandes volúmenes de datos. Esta técnica permite a las máquinas aprender patrones y realizar tareas complejas, como el reconocimiento de voz y la visión por computadora. Su capacidad para mejorar continuamente a medida que se le proporcionan más datos la convierte en una herramienta clave en diversas industrias, desde la salud....

Este artículo fue publicado como parte del Blogatón de ciencia de datos

Relacionado