Introducción
El tiempo es el factor más crítico que decide si una empresa subirá o bajará. Es por eso que vemos que las ventas en las tiendas y las plataformas de comercio electrónico se alinean con los festivales. Estas empresas analizan años de datos de gasto para comprender cuál es el mejor momento para abrir las puertas y ver un aumento en el gasto de los consumidores.
Pero, ¿cómo puede usted, como científico de datos, realizar este análisis? ¡No te preocupes, no necesitas construir una máquina del tiempo! El modelado de series de tiempo es una técnica poderosa que actúa como una puerta de entrada para comprender y pronosticar tendencias y patrones.
Pero incluso un modelo de serie temporalUna serie temporal es un conjunto de datos recogidos o medidos en momentos sucesivos, generalmente en intervalos de tiempo regulares. Este tipo de análisis permite identificar patrones, tendencias y ciclos en los datos a lo largo del tiempo. Su aplicación es amplia, abarcando áreas como la economía, la meteorología y la salud pública, facilitando la predicción y la toma de decisiones basadas en información histórica.... tiene diferentes facetas. La mayoría de los ejemplos que vemos en la web tratan con series de tiempo univariadas. Desafortunadamente, los casos de uso del mundo real no funcionan así. Hay múltiples variables en juego, y manejarlas todas al mismo tiempo es donde un científico de datos ganará su valor.
En este artículo, entenderemos qué es una serie de tiempo multivariante y cómo lidiar con ella. También tomaremos un estudio de caso y lo implementaremos en Python para brindarle una comprensión práctica del tema.
Tabla de contenido
- Series de tiempo univariadas versus multivariadas
- Serie de tiempo univariante
- Serie de tiempo multivariante
- Manejo de una serie temporal multivariante: regresión automática vectorial (VAR)
- ¿Por qué necesitamos VAR?
- Estacionariedad en una serie de tiempo multivariante
- División de validación de tren
- Implementación de Python
1. Series de tiempo univariadas versus multivariadas
Este artículo asume cierta familiaridad con las series de tiempo univariadas, sus propiedades y las diversas técnicas utilizadas para la predicción. Dado que este artículo se centrará en series de tiempo multivariadas, le sugiero que revise los siguientes artículos que sirven como una buena introducción a las series de tiempo univariadas:
Pero le daré un repaso rápido de lo que es una serie de tiempo univariante, antes de entrar en los detalles de una serie de tiempo multivariante. Veámoslos uno por uno para comprender la diferencia.
1.1 Serie de tiempo univariante
Una serie de tiempo univariante, como sugiere su nombre, es una serie con una única variableEn estadística y matemáticas, una "variable" es un símbolo que representa un valor que puede cambiar o variar. Existen diferentes tipos de variables, como las cualitativas, que describen características no numéricas, y las cuantitativas, que representan cantidades numéricas. Las variables son fundamentales en experimentos y estudios, ya que permiten analizar relaciones y patrones entre diferentes elementos, facilitando la comprensión de fenómenos complejos.... dependiente del tiempo.
Por ejemplo, eche un vistazo al conjunto de datos de muestra a continuación que consta de los valores de temperatura (cada hora), durante los últimos 2 años. Aquí, la temperatura es la variable dependiente (dependiente del tiempo).
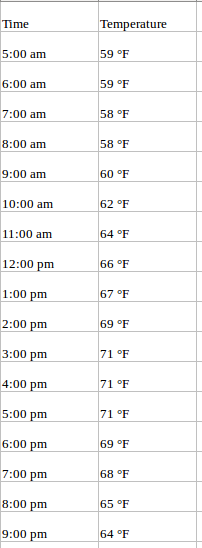
Si se nos pide que pronostiquemos la temperatura para los próximos días, observaremos los valores pasados e intentaremos medir y extraer un patrón. Notaríamos que la temperatura es más baja por la mañana y por la noche, mientras que alcanza su punto máximo por la tarde. Además, si tiene datos de los últimos años, observará que hace más frío durante los meses de noviembre a enero, mientras que es comparativamente más caluroso en abril a junio.
Tales observaciones nos ayudarán a predecir valores futuros. ¿Notó que usamos solo una variable (la temperatura de los últimos 2 años)? Por lo tanto, esto se denomina Análisis / Pronóstico de series de tiempo univariantes.
1.2 Serie de tiempo multivariante (MTS)
Una serie de tiempo multivariante tiene más de una variable dependiente del tiempo. Cada variable depende no solo de sus valores pasados, sino que también tiene cierta dependencia de otras variables. Esta dependencia se utiliza para pronosticar valores futuros. ¿Suena complicado? Dejame explicar.
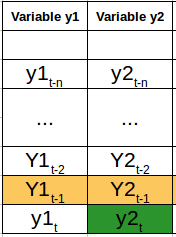
Considere el ejemplo anterior. Ahora suponga que nuestro conjunto de datos incluye el porcentaje de transpiración, el punto de rocío, la velocidad del viento, el porcentaje de cobertura de nubes, etc. junto con el valor de temperatura de los últimos dos años. En este caso, hay que considerar múltiples variables para predecir la temperatura de manera óptima. Una serie como esta entraría en la categoría de series de tiempo multivariadas. A continuación se muestra una ilustración de esto:
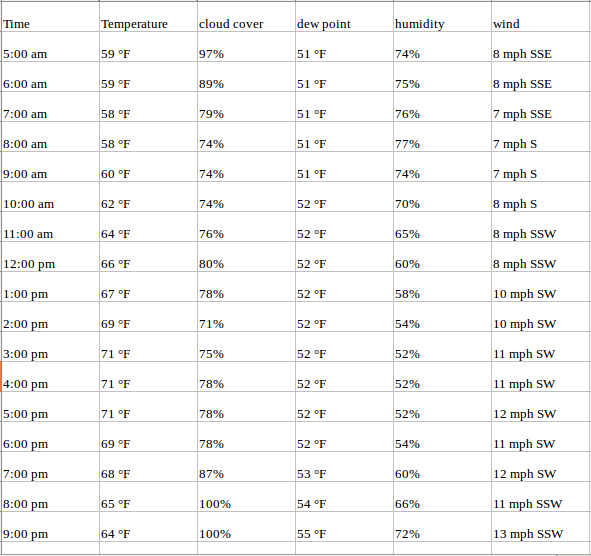
Ahora que entendemos cómo es una serie de tiempo multivariante, comprendamos cómo podemos usarla para construir un pronóstico.
2. Manejo de una serie temporal multivariante – VAR
En esta sección, le presentaré uno de los métodos más utilizados para el pronóstico de series de tiempo multivariante: Regresión automática vectorial (VAR).
En un modelo VAR, cada variable es una función lineal de los valores pasados de sí misma y los valores pasados de todas las demás variables. Para explicar esto de una mejor manera, voy a usar un ejemplo visual simple:
Tenemos dos variables, y1 e y2. Necesitamos pronosticar el valor de estas dos variables en el tiempo t, a partir de los datos dados para los n valores pasados. Para simplificar, he considerado que el valor de retraso es 1.
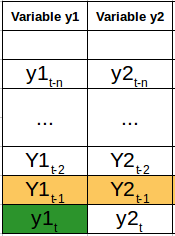
Para calcular y1
![]()
![]()
Aquí,
- a1 y a2 son los términos constantes,
- w11, w12, w21 y w22 son los coeficientes,
- e1 y e2 son los términos de error
Estas ecuaciones son similares a la ecuación de un proceso AR. Dado que el proceso AR se utiliza para datos de series de tiempo univariantes, los valores futuros son combinaciones lineales de sus propios valores pasados únicamente. Considere el proceso AR (1):
y
En este caso, tenemos solo una variable – y, un término constante – a, un término de error – e, y un coeficiente – w. Para acomodar los términos de múltiples variables en cada ecuación para VAR, usaremos vectores. Podemos escribir las ecuaciones (1) y (2) de la siguiente forma:
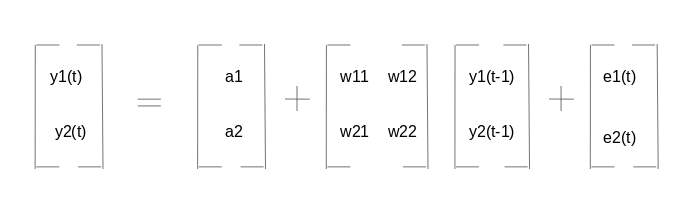
Las dos variables son y1 e y2, seguidas de una constante, una métrica de coeficiente, un valor de retraso y una métrica de error. Ésta es la ecuación vectorial para un proceso VAR (1). Para un proceso VAR (2), se agregará otro término vectorial para el tiempo (t-2) a la ecuación para generalizar para p rezagos:
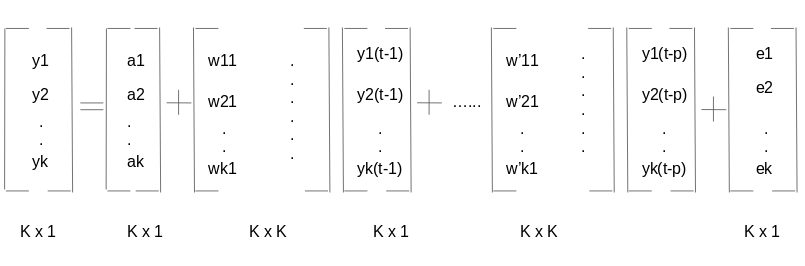
La ecuación anterior representa un proceso VAR (p) con variables y1, y2… yk. Lo mismo se puede escribir como:
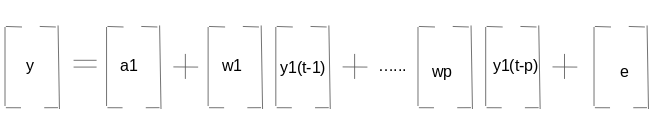
![]()
El término εt en la ecuación representa el ruido blanco vectorial multivariado. Para una serie de tiempo multivariante, εt debe ser un vector aleatorio continuo que satisfaga las siguientes condiciones:
- E (εt) = 0
El valor esperado para el vector de error es 0 - E (εt1, εt2‘) = σ12
Valor esperado de εt y εt‘es la desviación estándar de la serie
3. ¿Por qué necesitamos VAR?
Recuerde el ejemplo de pronóstico de temperaturas templadas que vimos anteriormente. Se puede argumentar que se tratará como una serie univariante múltiple. Podemos resolverlo usando métodos simples de pronóstico univariante como AR. Dado que el objetivo es predecir la temperatura, podemos simplemente eliminar las otras variables (excepto la temperatura) y ajustar un modelo a las series univariadas restantes.
Otra idea sencilla es pronosticar los valores de cada serie de forma individual utilizando las técnicas que ya conocemos. ¡Esto haría que el trabajo fuera extremadamente sencillo! Entonces, ¿por qué debería aprender otra técnica de pronóstico? ¿No es este tema lo suficientemente complicado ya?
De las ecuaciones anteriores (1) y (2), está claro que cada variable está usando los valores pasados de cada variable para hacer las predicciones. A diferencia de AR, VAR es capaz de comprender y utilizar la relación entre varias variables.. Esto es útil para describir el comportamiento dinámico de los datos y también proporciona mejores resultados de pronóstico. Además, implementar VAR es tan simple como usar cualquier otra técnica univariante (que verá en la última sección).
4. Estacionariedad de una serie temporal multivariante
Sabemos por el estudio del concepto univariado que una serie de tiempo estacionaria nos dará, en la mayoría de los casos, un mejor conjunto de predicciones. Si no está familiarizado con el concepto de estacionariedad, lea primero este artículo: Una introducción suave al manejo de series temporales no estacionarias.
Para resumir, para una serie de tiempo univariante dada:
y
Se dice que la serie es estacionaria si el valor de | c | <1. Ahora, recuerde la ecuación de nuestro proceso VAR:
![]()
Nota: I es la matriz de identidad.
Representar la ecuación en términos de Operadores de retraso, tenemos:
![]()
Tomando todos los términos y
![]()
![]()
El coeficiente de y
![]()
![]()
Para que una serie sea estacionaria, los valores propios de | Φ (L)-1| debe ser menor que 1 en módulo. Esto puede parecer complicado dado el número de variables en la derivación. Esta idea se ha explicado mediante un simple ejemplo numérico en el siguiente video. Le recomiendo que lo vea para solidificar su comprensión:
Similar a la prueba de Dickey-Fuller aumentada para series univariadas, tenemos la prueba de Johansen para verificar la estacionariedad de cualquier dato de series de tiempo multivariante. Veremos cómo realizar la prueba en el último apartado de este artículo.
5. División de validación de tren
Si ha trabajado anteriormente con datos de series de tiempo univariantes, conocerá los conjuntos de validación de trenes. La idea de crear un conjunto de validación es analizar el rendimiento del modelo antes de usarlo para hacer predicciones.
Crear un conjunto de validación para problemas de series de tiempo es complicado porque tenemos que tener en cuenta el componente de tiempo. Uno no puede usar directamente el train_test_split o k-fold validación, ya que esto interrumpirá el patrón en la serie. El conjunto de validación debe crearse teniendo en cuenta los valores de fecha y hora.
Suponga que tenemos que pronosticar la temperatura, el punto de rocío, el porcentaje de nubes, etc. para los próximos dos meses utilizando datos de los últimos dos años. Un método posible es mantener a un lado los datos de los últimos dos meses y entrenar el modelo en los 22 meses restantes.
Una vez que se ha entrenado el modelo, podemos usarlo para hacer predicciones sobre el conjunto de validación. Con base en estas predicciones y los valores reales, podemos verificar qué tan bien se desempeñó el modelo y las variables para las cuales el modelo no lo hizo tan bien. Y para hacer la predicción final, use el conjunto de datos completo (combine el tren y los conjuntos de validación).
6. Implementación de Python
En esta sección, implementaremos el modelo Vector AR en un conjunto de datos de juguetes. He utilizado el conjunto de datos de calidad del aire para esto y puede descargarlo de aquí.
#import required packages
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
#read the data
df = pd.read_csv("AirQualityUCI.csv", parse_dates=[['Date', 'Time']])
#check the dtypes
df.dtypes
Date_Time object CO(GT) int64 PT08.S1(CO) int64 NMHC(GT) int64 C6H6(GT) int64 PT08.S2(NMHC) int64 NOx(GT) int64 PT08.S3(NOx) int64 NO2(GT) int64 PT08.S4(NO2) int64 PT08.S5(O3) int64 T int64 RH int64 AH int64 dtype: object
El tipo de datos del Fecha y hora la columna es objeto y tenemos que cambiarlo a fecha y hora. Además, para preparar los datos, necesitamos que el índiceEl "Índice" es una herramienta fundamental en libros y documentos, que permite ubicar rápidamente la información deseada. Generalmente, se presenta al inicio de una obra y organiza los contenidos de manera jerárquica, incluyendo capítulos y secciones. Su correcta elaboración facilita la navegación y mejora la comprensión del material, convirtiéndolo en un recurso esencial tanto para estudiantes como para profesionales en diversas áreas.... tenga fecha y hora. Siga los siguientes comandos:
df['Date_Time'] = pd.to_datetime(df.Date_Time , format="%d/%m/%Y %H.%M.%S") data = df.drop(['Date_Time'], axis=1) data.index = df.Date_Time
El siguiente paso es lidiar con los valores perdidos. Dado que los valores perdidos en los datos se reemplazan con un valor -200, tendremos que imputar el valor faltante con un número mejor. Considere esto: si falta el valor actual del punto de rocío, podemos asumir con seguridad que estará cerca del valor de la hora anterior. Tiene sentido, ¿verdad? Aquí, imputaré -200 con el valor anterior.
Puede optar por sustituir el valor utilizando el promedio de algunos valores anteriores, o el valor a la misma hora el día anterior (puede compartir su (s) idea (s) de imputar valores faltantes en la sección de comentarios a continuación).
#missing value treatment cols = data.columns for j in cols: for i in range(0,len(data)): if data[j][i] == -200: data[j][i] = data[j][i-1] #checking stationarity from statsmodels.tsa.vector_ar.vecm import coint_johansen #since the test works for only 12 variables, I have randomly dropped #in the next iteration, I would drop another and check the eigenvalues johan_test_temp = data.drop([ 'CO(GT)'], axis=1) coint_johansen(johan_test_temp,-1,1).eig
A continuación se muestra el resultado de la prueba:
array([ 0.17806667, 0.1552133 , 0.1274826 , 0.12277888, 0.09554265,
0.08383711, 0.07246919, 0.06337852, 0.04051374, 0.02652395,
0.01467492, 0.00051835])
Ahora podemos seguir adelante y crear el conjunto de validación para que se ajuste al modelo y probar el rendimiento del modelo:
#creating the train and validation set train = data[:int(0.8*(len(data)))] valid = data[int(0.8*(len(data))):] #fit the model from statsmodels.tsa.vector_ar.var_model import VAR model = VAR(endog=train) model_fit = model.fit() # make prediction on validation prediction = model_fit.forecast(model_fit.y, steps=len(valid))
Las predicciones tienen la forma de una matriz, donde cada lista representa las predicciones de la fila. Transformaremos esto en un formato más presentable.
#converting predictions to dataframe
pred = pd.DataFrame(index=range(0,len(prediction)),columns=[cols])
for j in range(0,13):
for i in range(0, len(prediction)):
pred.iloc[i][j] = prediction[i][j]
#check rmse
for i in cols:
print('rmse value for', i, 'is : ', sqrt(mean_squared_error(pred[i], valid[i])))
Salida del código anterior:
rmse value for CO(GT) is : 1.4200393103392812 rmse value for PT08.S1(CO) is : 303.3909208229375 rmse value for NMHC(GT) is : 204.0662895081472 rmse value for C6H6(GT) is : 28.153391799471244 rmse value for PT08.S2(NMHC) is : 6.538063846286176 rmse value for NOx(GT) is : 265.04913993413805 rmse value for PT08.S3(NOx) is : 250.7673347152554 rmse value for NO2(GT) is : 238.92642219826683 rmse value for PT08.S4(NO2) is : 247.50612831072633 rmse value for PT08.S5(O3) is : 392.3129907890131 rmse value for T is : 383.1344361254454 rmse value for RH is : 506.5847387424092 rmse value for AH is : 8.139735443605728
Después de la prueba en el conjunto de validación, ajustemos el modelo en el conjunto de datos completo
#make final predictions model = VAR(endog=data) model_fit = model.fit() yhat = model_fit.forecast(model_fit.y, steps=1) print(yhat)
Notas finales
Antes de comenzar este artículo, la idea de trabajar con una serie de tiempo multivariante parecía desalentadora en su alcance. Es un tema complejo, así que tómate tu tiempo para comprender los detalles. La mejor manera de aprender es practicar, por lo que espero que la implementación de Python anterior le sea útil.
Le recomiendo que utilice este enfoque en un conjunto de datos de su elección. Esto consolidará aún más su comprensión de este tema complejo pero muy útil. Si tiene alguna sugerencia o consulta, compártala en la sección de comentarios.






