Introducción
Al crear un modelo de aprendizaje automático en la vida real, es casi raro que todas las variables del conjunto de datos sean útiles para crear un modelo. Agregar variables redundantes reduce la capacidad de generalización del modelo y también puede reducir la precisión general de un clasificador. Además, agregar más y más variables a un modelo aumenta la complejidad general del modelo.
Según el Ley de la parsimonia de ‘La navaja de Occam’, la mejor explicación a un problema es la que involucra la menor cantidad de supuestos posibles. Por lo tanto, la selección de características se convierte en una parte indispensable de la construcción de modelos de aprendizaje automático.
Objetivo
El objetivo de la selección de características en el aprendizaje automático es encontrar el mejor conjunto de características que le permita construir modelos útiles de los fenómenos estudiados.
Las técnicas para la selección de funciones en el aprendizaje automático se pueden clasificar en general en las siguientes categorías:
Técnicas supervisadas: Estas técnicas se pueden usar para datos etiquetados y se usan para identificar las características relevantes para aumentar la eficiencia de modelos supervisados como clasificación y regresión.
Técnicas no supervisadas: Estas técnicas se pueden utilizar para datos sin etiquetar.
Desde un punto de vista taxonómico, estas técnicas se clasifican en:
A. Métodos de filtrado
B. Métodos de envoltura
C. Métodos integrados
D. Métodos híbridos
En este artículo, analizaremos algunas técnicas populares de selección de funciones en el aprendizaje automático.
A. Métodos de filtrado
Los métodos de filtro recogen las propiedades intrínsecas de las características medidas a través de estadísticas univariadas en lugar del rendimiento de validación cruzada. Estos métodos son más rápidos y menos costosos computacionalmente que los métodos de envoltura. Cuando se trata de datos de alta dimensión"Dimensión" es un término que se utiliza en diversas disciplinas, como la física, la matemática y la filosofía. Se refiere a la medida en la que un objeto o fenómeno puede ser analizado o descrito. En física, por ejemplo, se habla de dimensiones espaciales y temporales, mientras que en matemáticas puede referirse a la cantidad de coordenadas necesarias para representar un espacio. Su comprensión es fundamental para el estudio y..., es computacionalmente más económico utilizar métodos de filtrado.
Analicemos algunas de estas técnicas:
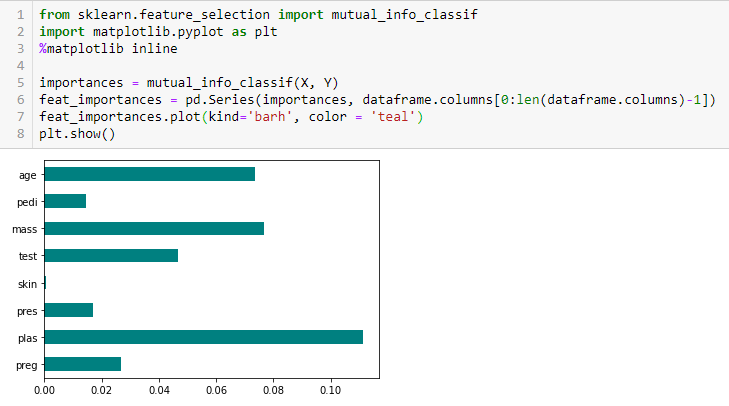
Ganancia de información
La ganancia de información calcula la reducción de la entropía a partir de la transformación de un conjunto de datos. Se puede utilizar para la selección de características evaluando la ganancia de información de cada variableEn estadística y matemáticas, una "variable" es un símbolo que representa un valor que puede cambiar o variar. Existen diferentes tipos de variables, como las cualitativas, que describen características no numéricas, y las cuantitativas, que representan cantidades numéricas. Las variables son fundamentales en experimentos y estudios, ya que permiten analizar relaciones y patrones entre diferentes elementos, facilitando la comprensión de fenómenos complejos.... en el contexto de la variable de destino.
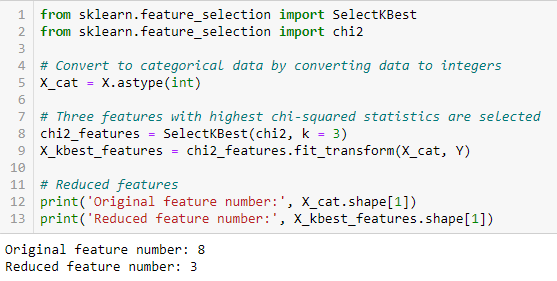
Prueba de chi-cuadrado
La prueba de chi-cuadrado se usa para características categóricas en un conjunto de datos. Calculamos Chi-cuadrado entre cada característica y el objetivo y seleccionamos el número deseado de características con las mejores puntuaciones de Chi-cuadrado. Para aplicar correctamente el chi-cuadrado para probar la relación entre varias características en el conjunto de datos y la variable objetivo, se deben cumplir las siguientes condiciones: las variables deben ser categórico, muestreado independientemente y los valores deben tener un frecuencia esperada mayor que 5.
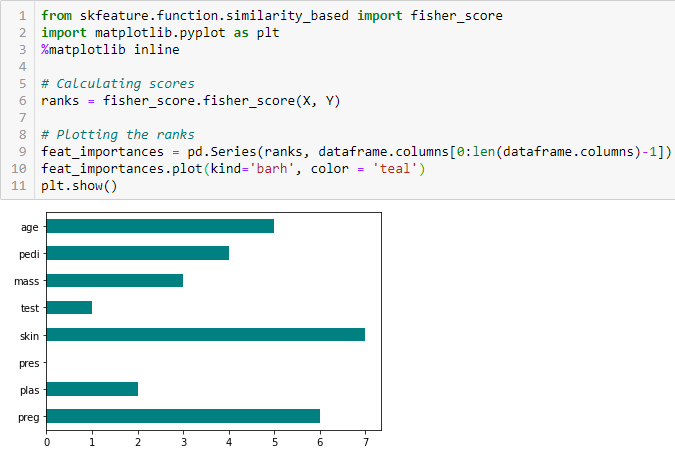
Puntuación de Fisher
La puntuación de Fisher es uno de los métodos de selección de características supervisadas más utilizados. El algoritmo que usaremos devuelve los rangos de las variables basados en la puntuación del pescador en orden descendente. Luego podemos seleccionar las variables según el caso.
Coeficiente de correlación
La correlación es una medidaLa "medida" es un concepto fundamental en diversas disciplinas, que se refiere al proceso de cuantificar características o magnitudes de objetos, fenómenos o situaciones. En matemáticas, se utiliza para determinar longitudes, áreas y volúmenes, mientras que en ciencias sociales puede referirse a la evaluación de variables cualitativas y cuantitativas. La precisión en la medición es crucial para obtener resultados confiables y válidos en cualquier investigación o aplicación práctica.... de la relación lineal de 2 o más variables. Mediante la correlación, podemos predecir una variable a partir de la otra. La lógica detrás del uso de la correlación para la selección de características es que las buenas variables están altamente correlacionadas con el objetivo. Además, las variables deben estar correlacionadas con el objetivo, pero no deben estar correlacionadas entre sí.
Si dos variables están correlacionadas, podemos predecir una a partir de la otra. Por lo tanto, si dos características están correlacionadas, el modelo realmente solo necesita una de ellas, ya que la segunda no agrega información adicional. Usaremos la correlación de Pearson aquí.
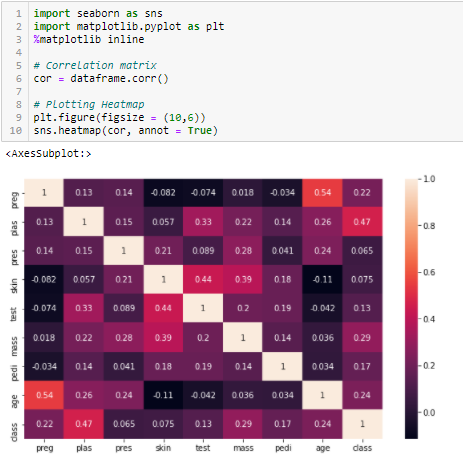
Necesitamos establecer un valor absoluto, digamos 0.5 como el umbral para seleccionar las variables. Si encontramos que las variables predictoras están correlacionadas entre sí, podemos descartar la variable que tiene un valor de coeficiente de correlación más bajo con la variable objetivo. También podemos calcular múltiples coeficientes de correlación para comprobar si más de dos variables están correlacionadas entre sí. Este fenómeno se conoce como multicolinealidad.
Umbral de varianza
El umbral de varianza es un enfoque de línea de base simple para la selección de características. Elimina todas las características cuya variación no alcanza algún umbral. De forma predeterminada, elimina todas las características de varianza cero, es decir, las características que tienen el mismo valor en todas las muestras. Suponemos que las características con una varianza más alta pueden contener información más útil, pero tenga en cuenta que no estamos teniendo en cuenta la relación entre las variables de característica o las variables de característica y objetivo, que es uno de los inconvenientes de los métodos de filtro.
Get_support devuelve un vector booleano donde True significa que la variable no tiene varianza cero.
Diferencia absoluta media (MAD)
‘La diferencia absoluta media (MAD) calcula la diferencia absoluta del valor medio. La principal diferencia entre las medidas de varianza y MAD es la ausencia del cuadrado en esta última. El MAD, al igual que la varianza, también es una variante de escala ». [1] Esto significa que a mayor DMA, mayor poder discriminatorio.
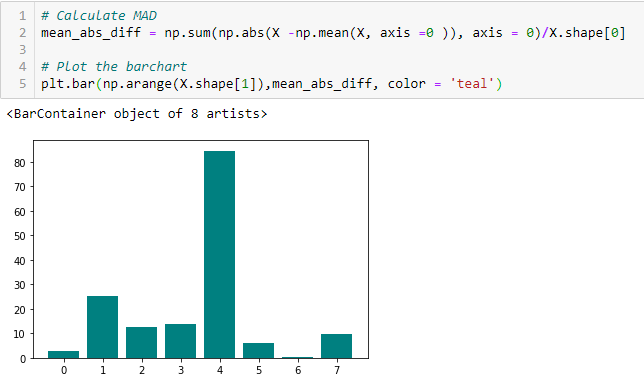
Relación de dispersión
‘Otra medida de dispersión aplica la media aritmética (AM) y la media geométrica (GM). Para una característica dada (positiva) XI en n patrones, AM y GM están dados por
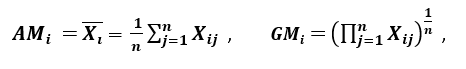
respectivamente; ya que SOYI ≥ GMI, con igualdad si y solo si Xi1 = Xi2 =…. = Xen, luego la proporción
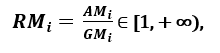
se puede utilizar como medida de dispersión. Una mayor dispersión implica un mayor valor de Ri, por lo que una característica más relevante. Por el contrario, cuando todas las muestras de características tienen (aproximadamente) el mismo valor, Ri está cerca de 1, lo que indica una característica de baja relevancia ‘. [1]
‘
B. Métodos de envoltura:
Los envoltorios requieren algún método para buscar en el espacio todos los posibles subconjuntos de características, evaluando su calidad aprendiendo y evaluando un clasificador con ese subconjunto de características. El proceso de selección de características se basa en un algoritmo de aprendizaje automático específico que intentamos encajar en un conjunto de datos determinado. Sigue un enfoque de búsqueda codiciosa al evaluar todas las posibles combinaciones de características contra el criterio de evaluación. Los métodos de envoltura generalmente dan como resultado una mejor precisión predictiva que los métodos de filtro.
Analicemos algunas de estas técnicas:
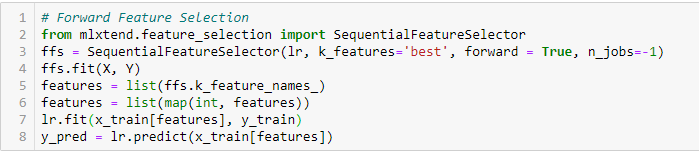
Selección de funciones avanzadas
Este es un método iterativo en el que comenzamos con la variable de mejor rendimiento contra el objetivo. A continuación, seleccionamos otra variable que ofrezca el mejor rendimiento en combinación con la primera variable seleccionada. Este proceso continúa hasta que se alcanza el criterio preestablecido.
Eliminación de características hacia atrás
Este método funciona exactamente de manera opuesta al método de selección de características hacia adelante. Aquí, comenzamos con todas las funciones disponibles y construimos un modelo. A continuación, tomamos la variable del modelo que da el mejor valor de medida de evaluación. Este proceso continúa hasta que se alcanza el criterio preestablecido.
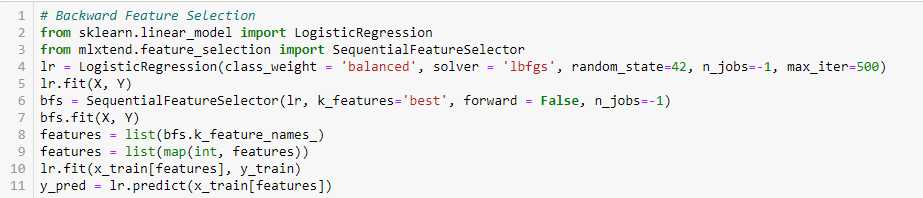
Este método, junto con el discutido anteriormente, también se conoce como el método de selección secuencial de características.
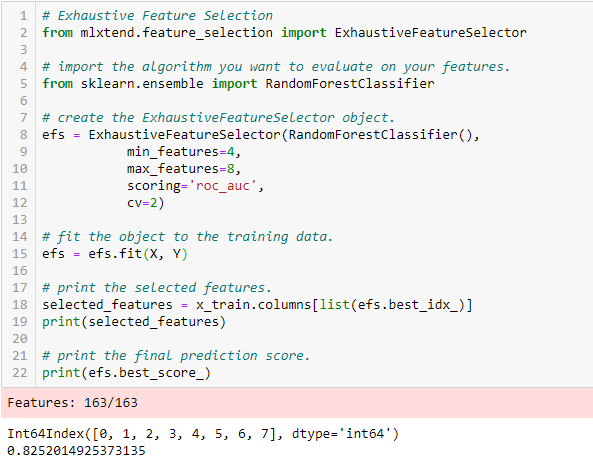
Selección exhaustiva de funciones
Este es el método de selección de características más sólido cubierto hasta ahora. Esta es una evaluación de fuerza bruta de cada subconjunto de características. Esto significa que intenta todas las combinaciones posibles de las variables y devuelve el subconjunto de mejor rendimiento.
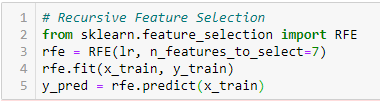
Eliminación de características recursivas
‘Dado un estimadorEl "Estimador" es una herramienta estadística utilizada para inferir características de una población a partir de una muestra. Se basa en métodos matemáticos para proporcionar estimaciones precisas y confiables. Existen diferentes tipos de estimadores, como los insesgados y los consistentes, que se eligen según el contexto y el objetivo del estudio. Su correcto uso es fundamental en investigaciones científicas, encuestas y análisis de datos.... externo que asigna pesos a las características (por ejemplo, los coeficientes de un modelo lineal), el objetivo de la eliminación de características recursivas (RFE) es seleccionar características considerando recursivamente conjuntos de características cada vez más pequeños. Primero, el estimador se entrena en el conjunto inicial de características y la importancia de cada característica se obtiene mediante un atributo coef_ o mediante un atributo feature_importances_.
Luego, las características menos importantes se eliminan del conjunto actual de características. Ese procedimiento se repite de forma recursiva en el conjunto podado hasta que finalmente se alcanza el número deseado de características para seleccionar. ‘[2]
C. Métodos integrados:
Estos métodos abarcan los beneficios de los métodos de envoltura y de filtro, al incluir interacciones de características pero también mantener un costo computacional razonable. Los métodos integrados son iterativos en el sentido de que se encargan de cada iteración del proceso de entrenamientoEl entrenamiento es un proceso sistemático diseñado para mejorar habilidades, conocimientos o capacidades físicas. Se aplica en diversas áreas, como el deporte, la educación y el desarrollo profesional. Un programa de entrenamiento efectivo incluye la planificación de objetivos, la práctica regular y la evaluación del progreso. La adaptación a las necesidades individuales y la motivación son factores clave para lograr resultados exitosos y sostenibles en cualquier disciplina.... del modelo y extraen cuidadosamente las características que más contribuyen al entrenamiento para una iteración en particular.
Analicemos algunas de estas técnicas, haga clic aquí:
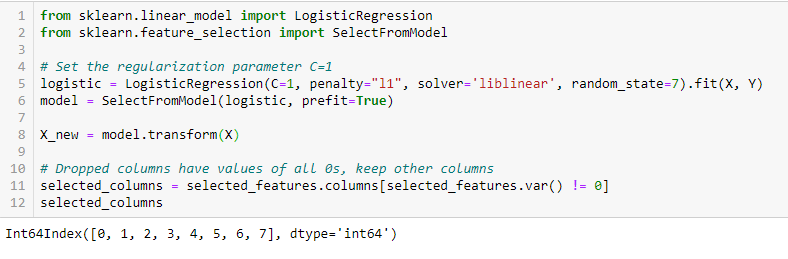
RegularizaciónLa regularización es un proceso administrativo que busca formalizar la situación de personas o entidades que operan fuera del marco legal. Este procedimiento es fundamental para garantizar derechos y deberes, así como para fomentar la inclusión social y económica. En muchos países, la regularización se aplica en contextos migratorios, laborales y fiscales, permitiendo a quienes se encuentran en situaciones irregulares acceder a beneficios y protegerse de posibles sanciones.... LASSO (L1)
La regularización consiste en agregar una penalización a los diferentes parámetrosLos "parámetros" son variables o criterios que se utilizan para definir, medir o evaluar un fenómeno o sistema. En diversos campos como la estadística, la informática y la investigación científica, los parámetros son fundamentales para establecer normas y estándares que guían el análisis y la interpretación de datos. Su adecuada selección y manejo son cruciales para obtener resultados precisos y relevantes en cualquier estudio o proyecto.... del modelo de aprendizaje automático para reducir la libertad del modelo, es decir, para evitar un ajuste excesivo. En la regularización de modelos lineales, la penalización se aplica sobre los coeficientes que multiplican cada uno de los predictores. De los diferentes tipos de regularización, Lasso o L1 tiene la propiedad de reducir algunos de los coeficientes a cero. Por lo tanto, esa característica se puede eliminar del modelo.
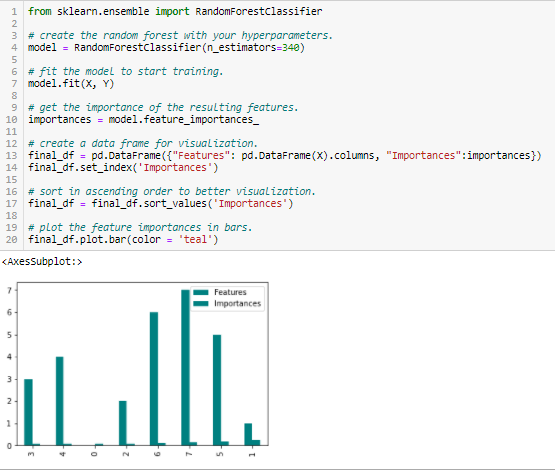
Importancia del bosque aleatorio
Random Forests es una especie de algoritmo de ensacado que agrega un número específico de árboles de decisión. Las estrategias basadas en árboles utilizadas por los bosques aleatorios se clasifican naturalmente según lo bien que mejoran la pureza del nodoNodo es una plataforma digital que facilita la conexión entre profesionales y empresas en busca de talento. A través de un sistema intuitivo, permite a los usuarios crear perfiles, compartir experiencias y acceder a oportunidades laborales. Su enfoque en la colaboración y el networking hace de Nodo una herramienta valiosa para quienes desean expandir su red profesional y encontrar proyectos que se alineen con sus habilidades y objetivos...., o en otras palabras, una disminución en la impureza (Impureza de gini) sobre todos los árboles. Los nodos con la mayor disminución de impurezas ocurren al comienzo de los árboles, mientras que las notas con la menor disminución de impurezas ocurren al final de los árboles. Por lo tanto, al podar árboles debajo de un nodo en particular, podemos crear un subconjunto de las características más importantes.
Conclusión
Hemos discutido algunas técnicas para la selección de funciones. Hemos dejado a propósito las técnicas de extracción de características como Análisis de Componentes Principales, Descomposición de Valor Singular, Análisis Discriminante Lineal, etc. Estos métodos ayudan a reducir la dimensionalidad de los datos o reducir el número de variables preservando la varianza de los datos.
Aparte de los métodos discutidos anteriormente, existen muchos otros métodos de selección de características. También existen métodos híbridos que utilizan técnicas de filtrado y envoltura. Si desea explorar más sobre las técnicas de selección de características, en mi opinión, un excelente material de lectura completo sería ‘Selección de funciones para el reconocimiento de patrones y datos«por Urszula Stańczyk y Lakhmi C. Jain.
Referencias
Documento denominado ‘Filtros de selección de características eficientes para datos de alta dimensión’ por Artur J. Ferreira, Mário AT Figueiredo [1]
https://scikit-learn.org/stable/modules/generated/sklearn.feature_selection.RFE.html%20%5b2%5d [2]
