Portfoliooptimierung in Python | Moderne Portfoliotheorie in Python

Einführung

In diesem Artikel, Wir lernen die Konzepte des Portfoliomanagements kennen und implementieren diese mithilfe von Python-Bibliotheken.

Der Artikel ist in drei Teile gegliedert, um die Grundlagen des Portfoliomanagements wie unten gezeigt abzudecken:

1. Rendite eines Vermögenswerts und eines Portfolios

2. Mit einem Vermögenswert und einem Portfolio verbundenes Risiko

3. Moderne Portfoliotheorie: das optimale Portfolio finden

Rendite eines Vermögenswerts und eines Portfolios

Bevor wir uns mit der Berechnung der Renditen eines Vermögenswerts und eines Portfolios befassen, Kommen wir kurz zur Definition von Portfolio und Rendite.

Aktentasche: Ein Portfolio ist eine Sammlung von Finanzinstrumenten wie Aktien, Fesseln, rohes Material, Zahlungsmittel und Zahlungsmitteläquivalente, sowie ihre Gegenstücke von Fonds. [Investopedia]

In diesem Artikel, Wir werden unser Portfolio haben, das enthält 4 Vermögenswerte (“Aktienorientiertes Portfolio“): Aktien von Apple Inc., Nike (NKC), Google und Amazon. Die Vorschau unserer Daten sehen Sie unten:

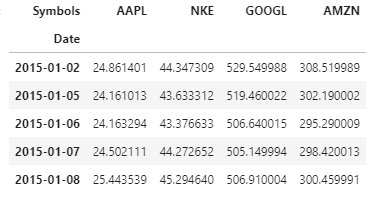
Kehrt zurück: Bezieht sich auf den Gewinn oder Verlust unserer Vermögenswerte / Portfolio für einen festen Zeitraum. In dieser Analyse, Wir erzielen eine Rendite als prozentuale Änderung des Schlusskurses des Vermögenswerts gegenüber dem Schlusskurs des Vortages. Wir berechnen die Rendite mit.pct_change () Funktion in Python.

Unten ist der Python-Code, um dasselbe zu tun und die 5 obere Reihen (Header) der Renditen

Notiz: die erste Zeile ist Null, wenn es keine vorherige Zeile gibt, um die Berechnung der prozentualen Änderung zu erleichtern.

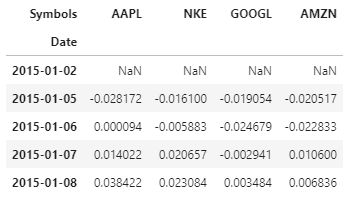
Rückgabe einer Brieftasche ist definiert als die gewichtete Summe der Renditen des Portfoliovermögens.

Um zu demonstrieren, wie man die Portfolioperformance in Python berechnet, Lassen Sie uns die Gewichte zufällig initialisieren (die wir dann optimieren). Die Portfoliorendite wird wie im folgenden Code gezeigt berechnet und die Kopfzeile der Portfoliorenditen wird ebenfalls angezeigt:

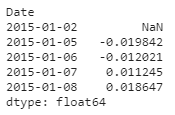
Wir haben gesehen, wie man Renditen berechnet, Jetzt lasst uns unseren Fokus auf ein anderes Konzept ändern: Risiko

Das mit Vermögenswerten und Portfolio verbundene Risiko

Die Methode zur Berechnung des Risikos eines Portfolios wird unten beschrieben und später erklären und geben wir die mathematische Formulierung für jeden der Schritte:

• Berechnen Sie die Kovarianzmatrix der Leistungsdaten.
• Annualisieren Sie die Kovarianz, indem Sie mit multiplizieren 252
• Berechnen Sie die Varianz des Portfolios, indem Sie es mit Gewichtsvektoren multiplizieren.
• Berechnen Sie die Quadratwurzel der oben berechneten Varianz, um die Standardabweichung zu erhalten. Diese Standardabweichung wird als Portfoliovolatilität bezeichnet..

Die Formel zur Berechnung der Kovarianz und deren Annualisierung lautet:

Kovarianz = return.cov () * 252

wie ist da 252 Werktage, wir multiplizieren die Kovarianz mit 252 um es zu annualisieren.

Die Variation des Portfolios, zu berechnen in Schritt 3 anterior, hängt von den Gewichten der Vermögenswerte im Portfolio ab und ist definiert als:

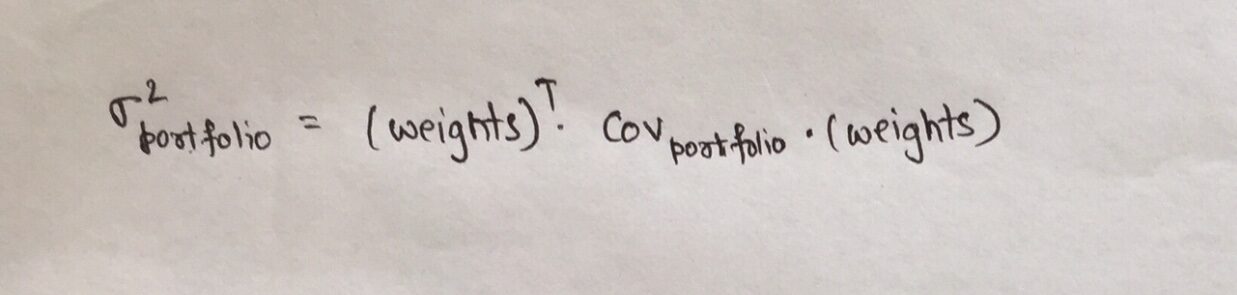
wo,

• Die_Aktentasche ist die Portfolio-Kovarianzmatrix
• Gewichte ist der Vektor der Gewichte, die jedem Vermögenswert im Portfolio zugewiesen werden

Unten ist der Ansatz zur Berechnung des Vermögensrisikos in Python.

Wie oben erklärt, wir multiplizieren die Kovarianzmatrix mit 252, weil dort sind 252 Handelstage im Jahr.

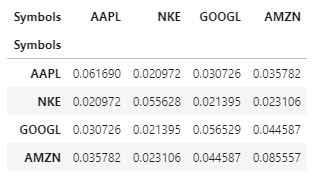
Die diagonalen Elemente von varnce_matrix repräsentieren die Varianz jedes Assets, während die Terme abseits der Diagonale die Kovarianz zwischen den beiden Vermögenswerten darstellen, zum Beispiel: das Element (1,2) repräsentiert die Kovarianz zwischen Nike und Apple.

Der Code zur Berechnung des Portfoliorisikos in Python, deren Methode wir vorhin gesehen haben, ist wie abgebildet:

Jetzt, die aufgabe ist für uns die gewichte zu optimieren. Warum? Damit wir unsere Rendite maximieren oder unser Risiko minimieren können, Und das tun wir mit moderner Portfoliotheorie!!

Moderne Portfoliotheorie

Die moderne Portfoliotheorie besagt, dass die Risiko- und Renditemerkmale einer Anlage nicht allein betrachtet werden sollten, Sie sollten vielmehr danach bewertet werden, wie sich die Anlage auf das Gesamtrisiko und die Gesamtrendite des Portfolios auswirkt.. MPT zeigt, dass ein Anleger ein Portfolio aus mehreren Vermögenswerten aufbauen kann, das die Renditen bei einem bestimmten Risikoniveau maximiert.. in Ergänzung, ein gewünschtes Niveau der erwarteten Rendite gegeben, ein Investor kann ein Portfolio mit dem geringstmöglichen Risiko aufbauen. Basierend auf statistischen Maßen wie Varianz und Korrelation, Die Performance eines einzelnen Anlegers ist weniger wichtig als die Auswirkung auf das gesamte Portfolio. [Investopedia]

Diese Theorie wird im Folgenden zusammengefasst Abbildung"Abbildung" ist ein Begriff, der in verschiedenen Zusammenhängen verwendet wird, Von der Kunst zur Anatomie. Im künstlerischen Bereich, bezieht sich auf die Darstellung menschlicher oder tierischer Formen in Skulpturen und Gemälden. In der Anatomie, bezeichnet die Form und Struktur des Körpers. Was ist mehr, in der Mathematik, "Abbildung" Es hängt mit geometrischen Formen zusammen. Seine Vielseitigkeit macht es zu einem grundlegenden Konzept in mehreren Disziplinen..... Wir finden die Grenze wie unten gezeigt und maximieren die erwartete Rendite für das Risikoniveau oder minimieren das Risiko für ein bestimmtes erwartetes Renditeniveau.

Unser Ziel ist es, die Gewichtungen für jeden Vermögenswert in unserem Portfolio so zu wählen, dass wir die erwartete Rendite bei gegebenem Risikoniveau maximieren..

Mathematisch, die Zielfunktion kann wie unten gezeigt definiert werden:

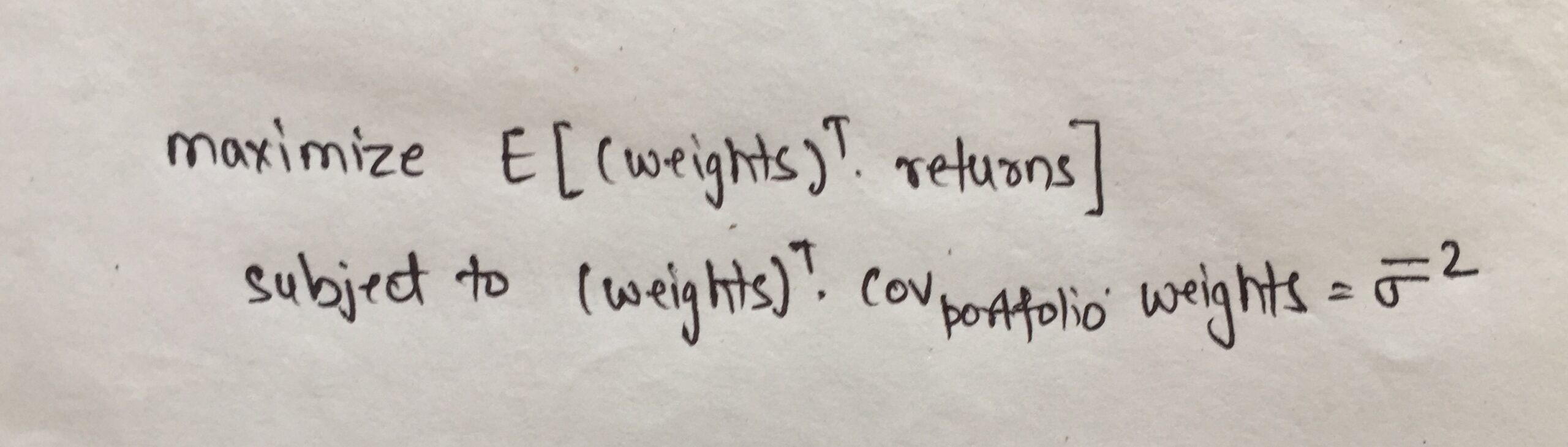
Eine andere Sichtweise auf die Effizienzgrenze und die Zielfunktion besteht darin, dass wir das Risiko minimieren können, wenn die erwartete Rendite mindestens über dem angegebenen Wert liegt.. Mathematisch, diese Zielfunktion kann geschrieben werden als:

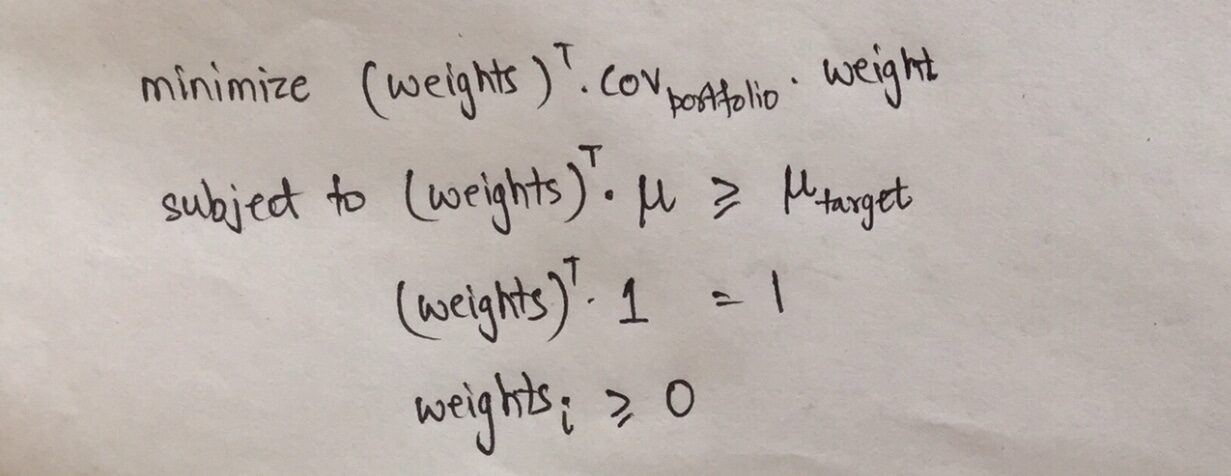
die erste Linie stellt dar, dass das Ziel darin besteht, die Varianz des Portfolios zu minimieren, nämlich, wiederum die Volatilität des Portfolios und, deshalb, Risiko minimieren.

Eingeschränkt bedeutet, dass die Renditen größer als eine bestimmte Zielrendite sein müssen, alle Gewichte müssen addieren 1 und die Gewichte dürfen nicht negativ sein.

Jetzt kennen wir das Konzept, Kommen wir jetzt zum praktischen Teil!

Zuerst, wir erzeugen die effiziente Grenze, indem wir eine Schleife ausführen. In jedem Zyklus, Wir betrachten einen anderen Satz zufällig zugewiesener Gewichtungen für die Vermögenswerte in unserem Portfolio und berechnen die Rendite und Volatilität für diese Kombination von Gewichten.

Dafür erstellen wir 3 leere Listen, einer zum Aufbewahren von Retouren, ein weiterer zum Speichern der Volatilität und der letzte zum Speichern von Portfoliogewichtungen.

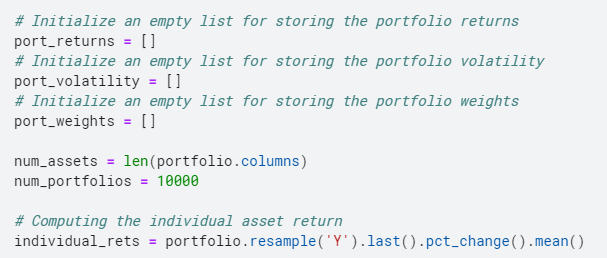
Sobald wir die Listen erstellt haben, Wir generieren die Gewichte unserer Vermögenswerte nach dem Zufallsprinzip wiederholt, dann normalisieren wir die Gewichtung um zu addieren 1. Dann berechnen wir die Renditen wie oben berechnet. Anschließend, Wir berechnen die Varianz des Portfolios und ziehen dann die Quadratwurzel und dann annualisieren sie, um die Volatilität zu erhalten, das messenDas "messen" Es ist ein grundlegendes Konzept in verschiedenen Disziplinen, , die sich auf den Prozess der Quantifizierung von Eigenschaften oder Größen von Objekten bezieht, Phänomene oder Situationen. In Mathematik, Wird verwendet, um Längen zu bestimmen, Flächen und Volumina, In den Sozialwissenschaften kann es sich auf die Bewertung qualitativer und quantitativer Variablen beziehen. Die Messgenauigkeit ist entscheidend, um zuverlässige und valide Ergebnisse in der Forschung oder praktischen Anwendung zu erhalten.... Risiko für unser Portfolio.

Jetzt aggregieren wir die Daten in einem Wörterbuch und erstellen dann einen Datenrahmen, um die Kombination von Asset-Gewichtungen und den entsprechenden Renditen und Volatilitäten zu sehen, die sie generieren.

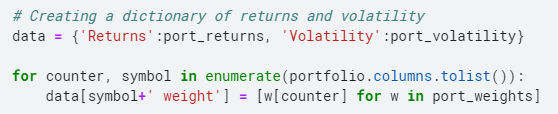
Hier ist die Vorschau der Rentabilitätsdaten, Portfoliovolatilität und -gewichte.

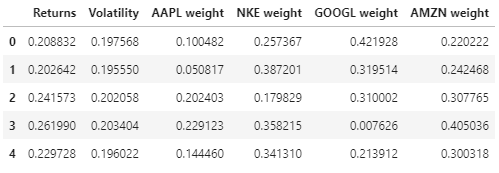
Jetzt haben wir alles dabei, um in die letzte Runde dieses Rennens einzusteigen und den optimalen Gewichtssatz zu finden!!

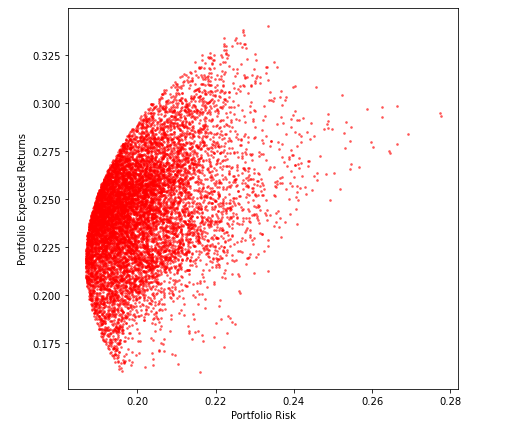
Wir stellen die Volatilität gegen die zuvor berechneten Renditen, Dies wird uns die Efficient Frontier geben, die wir zu Beginn dieses Artikels erstellen wollten.

Und es geht los!!

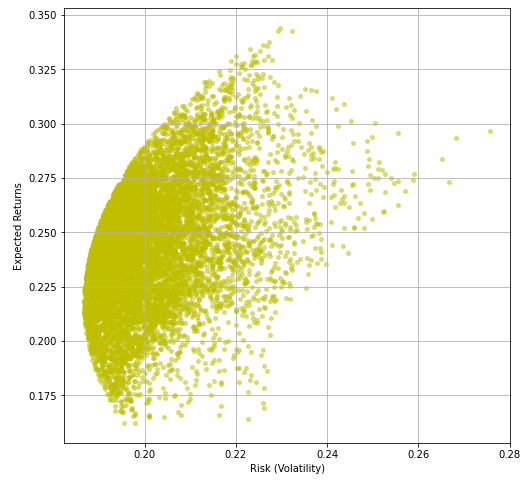
Jetzt haben wir die Efficient Frontier bei uns, Lass uns die optimalen Gewichte finden.

Wir können den Einsatz verschiedener Methoden wie unten beschrieben optimieren:

• Portfolio mit minimaler Volatilität (Risiko)
• Optimales Portfolio (Sharpe maximales Verhältnis)
• Maximale Rendite auf Risikoniveau; Minimales Risiko bei erwarteter Rendite; Portfolio mit der höchsten Sortino-Quote

In diesem Artikel werde ich durch die ersten beiden Ansätze optimieren. Im dritten Segment, das ‚Rendimiento máximo a un nivel de riesgo‘ und das ‚Minimales Risiko bei erwarteter Rendite‘ sie sind ganz einfach, Während derjenige, der auf dem IndexDas "Index" Es ist ein grundlegendes Werkzeug in Büchern und Dokumenten, Dies ermöglicht es Ihnen, die gewünschten Informationen schnell zu finden. Allgemein, Sie wird am Anfang einer Arbeit präsentiert und organisiert die Inhalte hierarchisch, mit Kapiteln und Abschnitten. Die richtige Vorbereitung erleichtert die Navigation und verbessert das Verständnis des Materials, was es zu einer unverzichtbaren Ressource sowohl für Studenten als auch für Fachleute in verschiedenen Bereichen macht.... ähnelt dem Sharpe-Index.

1. Mindestvolatilität

Um die Kombination der minimalen Volatilität zu finden, Wir wählen die Zeile in unserem Datenrahmen aus, die der minimalen Varianz entspricht, und finden diese Zeile mit der .idxmin-Funktion (). Der Code, um dasselbe zu tun, ist unten gezeigt:

Die Gewichte, die wir daraus erhalten, sind:

Jetzt, Finden Sie heraus, wo der niedrigste Punkt der Volatilität auf der obigen Kurve liegt. Die Antwort wird am Ende angezeigt! Aber betrüge nicht!

2. Höheres Schärfeverhältnis

Der Sharpe-Index ist die durchschnittliche Rendite, die über dem risikofreien Zinssatz pro Volatilitäts- oder Gesamtrisikoeinheit liegt.. Die Formel zur Berechnung des Sharpe-Verhältnisses ist unten angegeben:

Schärfeverhältnis = (R_Seite – R_F)/ DAKOTA DEL ON_Seite

wo,

• R_Seite ist die Rendite des Portfolios
• R_F ist der risikofreie Zinssatz
• Dakota del Sur_Seite ist die Standardabweichung der Portfoliorenditen

Der Code zur Berechnung des optimalen Portfolios, nämlich, Portfolio mit dem höchsten Sharpe-Index, unten gezeigt:

Dann, Portfoliogewichtungen, die den höchsten Sharpe-Index ergeben, werden angezeigt:

Finden Sie heraus, wo sich der höchste Punkt der Sharpe-Beziehung auf der obigen Kurve befindet. Die Antwort ist unten gezeigt! Ein Mal noch, Betrüge nicht!

Wie versprochen hier die Antwort auf die beiden obigen Fragen!!

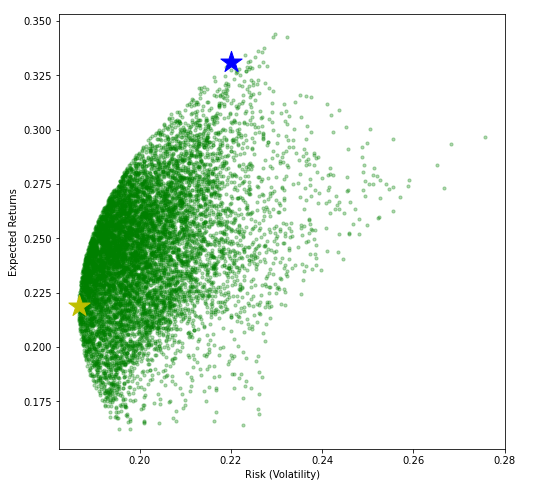
Der blaue Stern entspricht dem höchsten Sharpe-Beziehungspunkt und der gelbe Stern entspricht dem Punkt minimaler Volatilität.

Jetzt, bevor Sie diesen Artikel beenden, le animo a encontrar la cartera de Rentabilidad Máxima a un nivel de riesgo ‚Ja‘ Riesgo Mínimo a un Nivel de Rentabilidad Esperada ‚y marcarlos en el gráfico anterior.

Zusätzlich zur Verwendung der Sharpe-Beziehung, Wir können das Portfolio auch mit der Sortino-Relation optimieren.

Kurz darüber geben:

das Sortino-Beziehung ist eine Variation des Sharpe-Index, die schädliche Volatilität von der Gesamtvolatilität unterscheidet, indem sie die Asset-Standardabweichung negativer Portfoliorenditen verwendet (Abweichung nach unten) statt der Gesamtstandardabweichung der Portfoliorenditen. Die Sortino-Ratio nimmt die Rendite eines Vermögenswerts oder Portfolios und subtrahiert den risikofreien Zinssatz, und dann dividiere diesen Betrag durch die Abwärtsdrift des Vermögenswerts. [Investopedia]

Sortierverhältnis = (R_Seite – R_F)/ DAKOTA DEL OND

wo,

• R_Seite ist die Rendite des Portfolios
• R_F ist der risikofreie Zinssatz
• Dakota del SurD ist die Standardabweichung des Handicaps

Falls Sie Probleme bei der Implementierung oder dem Verständnis haben 3 Optimierungsmethoden, die ich oben beschrieben habe, schreib mir an [E-Mail geschützt] | [E-Mail geschützt] | oder kontaktieren Sie LinkedIn unter https://www.linkedin.com/in/parth-tyagi-4b867452/

Hinweis zum Autor: Parth Tyagi studiert derzeit PGDBA am IIM Kalkutta, IIT Kharagpur & Indian Statistical Institute-Kolkata und hat den B.Tech vom IIT Delhi abgeschlossen. Hat ~ 4 Jahre Berufserfahrung im Bereich Advanced Analytics.

Verwandt