Lineare vs. logistische Regression | Lineare und logistische Regression

Dieser Artikel wurde im Rahmen der Data Science Blogathon.

Einführung

Auf dieses Thema werde ich weiter unten ausführlich eingehen..

Schritte der linearen Regression

Wie der Name schon sagt, Die Idee hinter der linearen Regression ist, dass wir zu einer linearen Gleichung gelangen sollten, die die Beziehung zwischen den abhängigen und unabhängigen Variablen beschreibt.

Paso 1

Supongamos que tenemos un conjunto de datos donde x es la VariableIn Statistik und Mathematik, ein "Variable" ist ein Symbol, das einen Wert darstellt, der sich ändern oder variieren kann. Es gibt verschiedene Arten von Variablen, und qualitativ, die nicht-numerische Eigenschaften beschreiben, und quantitative, numerische Größen darstellen. Variablen sind grundlegend in Experimenten und Studien, da sie die Analyse von Beziehungen und Mustern zwischen verschiedenen Elementen ermöglichen, das Verständnis komplexer Phänomene zu erleichtern.... independiente e Y es una función de x (Ja= f (x)). Deswegen, Mit Hilfe der linearen Regression können wir die folgende Gleichung bilden (Gleichung für die beste Anpassungslinie):

Y = mx + C

Dies ist eine Geradengleichung, wobei m die Steigung der Geraden und c der Achsenabschnitt ist.

Paso 2

Jetzt, um die Best-Fit-Linie abzuleiten, zuerst weisen wir my und c zufällige Werte zu und berechnen den entsprechenden Wert von Y für ein gegebenes x. Dieser Y-Wert ist der Ausgabewert.

Paso 3

Wie die logistische Regression ein überwachter maschineller Lernalgorithmus ist, wir kennen bereits den Wert von reellem Y (abhängige Variable). Jetzt, da wir unseren berechneten Ausgabewert haben (lass es uns darstellen als ŷ), wir können überprüfen, ob unsere Vorhersage richtig ist oder nicht.

Bei linearer Regression, Wir berechnen diesen Fehler (Restwert) mit der MSE-Methode (mittlerer quadratischer Fehler) y lo denominamos Verlust-FunktionDie Verlustfunktion ist ein grundlegendes Werkzeug des maschinellen Lernens, das die Diskrepanz zwischen Modellvorhersagen und tatsächlichen Werten quantifiziert. Ziel ist es, den Trainingsprozess zu steuern, indem dieser Unterschied minimiert wird, Dadurch kann das Modell effektiver lernen. Es gibt verschiedene Arten von Verlustfunktionen, wie z. B. mittlerer quadratischer Fehler und Kreuzentropie, jeder für unterschiedliche Aufgaben geeignet und...:

Die Verlustfunktion kann geschrieben werden als:

L = 1 / n ∑ ((Ja – ŷ)²)

Wobei n die Anzahl der Beobachtungen ist.

Paso 4

Um die beste Passform zu erreichen, wir müssen den Wert der Verlustfunktion minimieren.

Um die Verlustfunktion zu minimieren, utilizamos una técnica llamada descenso de SteigungGradient ist ein Begriff, der in verschiedenen Bereichen verwendet wird, wie Mathematik und Informatik, um eine kontinuierliche Variation von Werten zu beschreiben. In Mathematik, bezieht sich auf die Änderungsrate einer Funktion, während des Studiums im Grafikdesign, Gilt für den Farbübergang. Dieses Konzept ist unerlässlich, um Phänomene wie die Optimierung von Algorithmen und die visuelle Darstellung von Daten zu verstehen, ermöglicht eine bessere Interpretation und Analyse in....

Lassen Sie uns analysieren, wie der Gradientenabstieg funktioniert (obwohl ich nicht auf die Details eingehen werde, da dies nicht der Schwerpunkt dieses Artikels ist).

Gradientenabstieg

Betrachten wir die Formel für die Verlustfunktion, das ‚mittlerer quadratischer Fehler‘ bedeutet, dass der Fehler in Termen zweiter Ordnung dargestellt wird.

Wenn wir die Verlustfunktion für das Gewicht grafisch darstellen (in unserer Gleichung sind die Gewichte myc), wird eine parabolische Kurve sein. Jetzt wo unser Fahrrad die Verlustfunktion minimieren soll, wir müssen das ende der kurve erreichen.

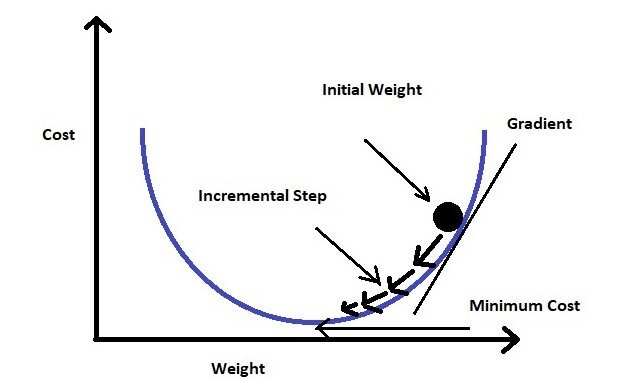
Um das zu erreichen, wir müssen die Ableitung erster Ordnung der Verlustfunktion für die Gewichte nehmen (mein C). Dann subtrahieren wir das Ergebnis der Ableitung des Anfangsgewichts durch Multiplizieren mit einer Lernrate (ein). Wir werden diesen Schritt so lange wiederholen, bis wir den Mindestwert erreicht haben (wir nennen es globale minima). Wir setzen einen Schwellenwert von einem sehr kleinen Wert (Beispiel: 0.0001) als globales Minimum. Wenn wir den Schwellenwert nicht festlegen, es kann ewig dauern, bis der genaue Nullwert erreicht ist.

Paso 5

Sobald die Verlustfunktion minimiert ist, wir erhalten die endgültige Gleichung für die beste Anpassungsgerade und können den Wert von Y für jedes gegebene X vorhersagen.

Hier endet die lineare Regression und wir sind nur noch einen Schritt von der logistischen Regression entfernt..

Logistische Regression

Wie ich bereits gesagt habe, grundsätzlich, logistische Regression wird verwendet, um Elemente einer Menge in zwei Gruppen zu klassifizieren (binäre Klassifikation) Berechnung der Wahrscheinlichkeit jedes Elements der Menge.

Schritte der logistischen Regression

In der logistischen Regression, wir bestimmen eine Wahrscheinlichkeitsschwelle. Wenn die Wahrscheinlichkeit eines bestimmten Elements größer als die Wahrscheinlichkeitsschwelle ist, wir klassifizieren dieses Element in eine Gruppe oder umgekehrt.

Paso 1

Um die binäre Trennung zu berechnen, erste, Wir bestimmen die am besten angepasste Linie nach den Schritten der linearen Regression.

Paso 2

Die Regressionsgerade, die wir aus der linearen Regression erhalten, ist sehr anfällig für Ausreißer. Deswegen, wird keine gute Arbeit leisten, zwei Klassen zu klassifizieren.

Deswegen, der vorhergesagte Wert wird in Wahrscheinlichkeit umgewandelt, indem er der Sigmoidfunktion zugeführt wird.

Die Sigmoid-Gleichung:

Wie wir in Abb. sehen können. 3, Wir können der Sigmoid-Funktion eine beliebige reelle Zahl zuführen und sie gibt einen Wert zwischen zurück 0 Ja 1.

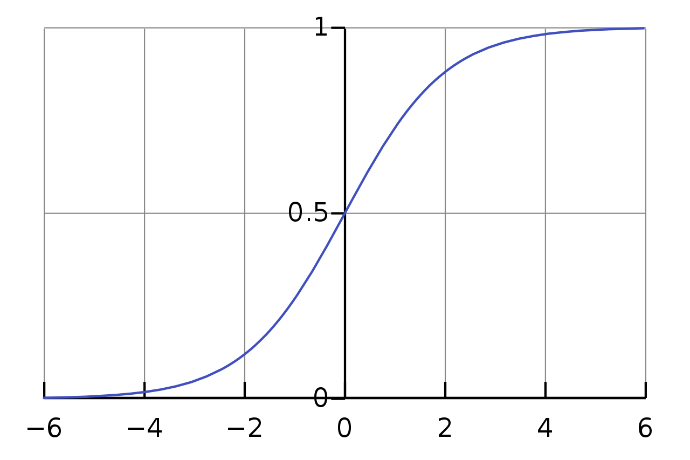
Feige 2: Sigmoidkurve (Bild aus Wikipedia)

Deswegen, wenn wir die Ausgabe füttern ŷ Wert auf die Sigmoidfunktion stimmt einen Wahrscheinlichkeitswert zwischen 0 Ja 1.

Paso 3

Schließlich, der Ausgabewert der Sigmoidfunktion wird 0 Ö 1 (diskrete Werte) nach dem Schwellenwert. Wie gewöhnlich, wir setzen den Schwellenwert auf 0,5. Daher, wir erhalten die binäre Klassifikation.

Jetzt haben wir die Grundidee, wie lineare Regression und logistische Regression zusammenhängen, Sehen wir uns den Prozess an einem Beispiel an.

Beispiel

Stellen Sie sich ein Problem vor, bei dem uns ein Datensatz zur Verfügung gestellt wird, der die Größe und das Gewicht einer Gruppe von Personen enthält. Unsere Aufgabe ist es, das Gewicht für neue Einträge in der Spalte Höhe vorherzusagen.

Wir können also herausfinden, dass dies ein Regressionsproblem ist, bei dem wir ein lineares Regressionsmodell erstellen. Wir werden das Modell mit den angegebenen Größen- und Gewichtswerten trainieren. Sobald das Modell trainiert ist, wir können das Gewicht für einen gegebenen unbekannten Höhenwert vorhersagen.

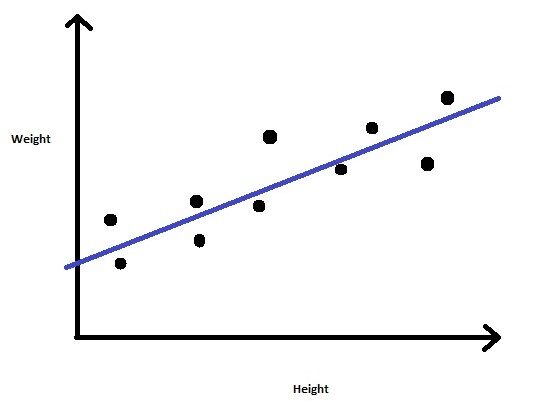
Feige 3: Lineare Regression

Angenommen, wir haben ein zusätzliches Feld Fettleibigkeit und wir müssen anhand ihrer Größe und ihres Gewichts klassifizieren, ob eine Person fettleibig ist oder nicht. Dies ist eindeutig ein Klassifizierungsproblem, bei dem wir den Datensatz in zwei Klassen aufteilen müssen (fettleibig und nicht fettleibig).

Dann, für das neue problem, wir können die Schritte der linearen Regression erneut durchlaufen und eine Regressionslinie konstruieren. Diesmal, la línea se basará en dos ParameterDas "Parameter" sind Variablen oder Kriterien, die zur Definition von, ein Phänomen oder System zu messen oder zu bewerten. In verschiedenen Bereichen wie z.B. Statistik, Informatik und naturwissenschaftliche Forschung, Parameter sind entscheidend für die Etablierung von Normen und Standards, die die Datenanalyse und -interpretation leiten. Ihre richtige Auswahl und Handhabung sind entscheidend, um genaue und relevante Ergebnisse in jeder Studie oder jedem Projekt zu erhalten.... Altura y Peso y la línea de regresión se ajustará entre dos conjuntos de valores discretos. Da diese Regressionsgerade sehr anfällig für Ausreißer ist, dient nicht dazu, zwei Klassen zu klassifizieren.

Um ein besseres Ranking zu bekommen, wir füttern die Ausgabewerte der Regressionsgerade in die Sigmoidfunktion. Die Sigmoidfunktion gibt die Wahrscheinlichkeit jedes Ausgabewerts der Regressionsgerade zurück. Jetzt, basierend auf einem vordefinierten Schwellenwert, Wir können die Ausgabe leicht in zwei Klassen von fettleibig oder nicht fettleibig einteilen.

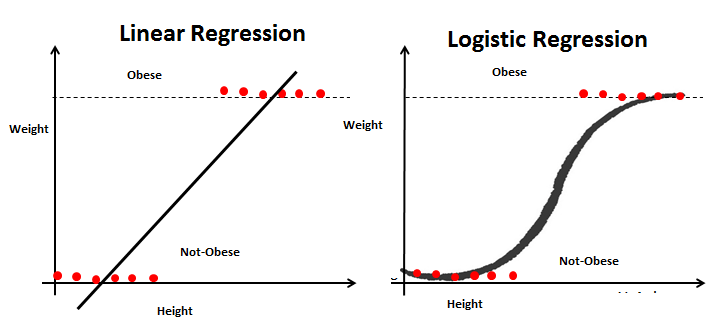
Schließlich, Wir können die Ähnlichkeiten und Unterschiede zwischen diesen beiden Modellen zusammenfassen.

Die Ähnlichkeiten zwischen linearer Regression und logistischer Regression

• Sowohl die lineare Regression als auch die logistische Regression sind überwachte maschinelle Lernalgorithmen.
• Lineare Regression und logistische Regression, beide Modelle sind parametrische Regression, nämlich, beide Modelle verwenden lineare Gleichungen für Vorhersagen.

Das sind alle Ähnlichkeiten, die wir zwischen diesen beiden Modellen haben.

Aber trotzdem, in Bezug auf die Funktionalität, diese beiden sind komplett verschieden. Unten sind die Unterschiede.

Unterschiede zwischen linearer Regression und logistischer Regression

• Lineare Regression wird verwendet, um Regressionsprobleme zu behandeln, während die logistische Regression verwendet wird, um Klassifikationsprobleme zu behandeln.
• Lineare Regression bietet kontinuierliche Ausgabe, aber die logistische Regression liefert eine diskrete Ausgabe.
• Der Zweck der linearen Regression besteht darin, die am besten passende Gerade zu finden, während die logistische Regression einen Schritt voraus ist und die Werte der Linie an die Sigmoidkurve anpasst.
• Die Methode zur Berechnung der Verlustfunktion bei der linearen Regression ist der quadratische Mittelwertfehler, während es für die logistische Regression die Maximum-Likelihood-Schätzung ist.

Notiz: Beim Schreiben dieses Artikels, Ich ging davon aus, dass der Leser bereits mit dem Grundkonzept der linearen Regression und der logistischen Regression vertraut ist. Ich hoffe, dieser Artikel erklärt die Beziehung zwischen diesen beiden Konzepten.

Verwandt