Cet article a été publié dans le cadre du Blogathon sur la science des données.
introduction
L'analyse de cluster ou le clustering est un algorithme d'apprentissage automatique non supervisé qui regroupe des ensembles de données non étiquetés. Son objectif est de former des clusters ou des groupes en utilisant les points de données d'un ensemble de données de manière à ce qu'il y ait une forte similarité entre les clusters et une faible similarité entre les clusters.. En termes simples, le clustering vise à former des sous-ensembles ou des groupes au sein d'un ensemble de données constitué de points de données qui sont en fait similaires les uns aux autres et les groupes ou sous-ensembles ou clusters formés peuvent différer considérablement les uns des autres.
pourquoi groupe?
Supposons que nous ayons un ensemble de données et que nous n'en sachions rien. Ensuite, un algoritmo de regroupementLe "regroupement" Il s’agit d’un concept qui fait référence à l’organisation d’éléments ou d’individus en groupes ayant des caractéristiques ou des objectifs communs. Ce procédé est utilisé dans diverses disciplines, y compris la psychologie, Éducation et biologie, faciliter l’analyse et la compréhension de comportements ou de phénomènes. Dans le domaine de l’éducation, par exemple, Le regroupement peut améliorer l’interaction et l’apprentissage entre les élèves en encourageant le travail.. puede descubrir grupos de objetos donde las distancias promedio entre los miembros / les points de données de chaque groupe sont plus proches que les membres / points de données dans d'autres groupes.
Certaines des applications pratiques du clustering dans la vie réelle comme:
1) SegmentaciónLa segmentation est une technique de marketing clé qui consiste à diviser un large marché en groupes plus petits et plus homogènes. Cette pratique permet aux entreprises d’adapter leurs stratégies et leurs messages aux spécificités de chaque segment, améliorant ainsi l’efficacité de vos campagnes. Le ciblage peut se faire sur des critères démographiques, Psychographique, géographique ou comportementale, Faciliter une communication plus pertinente et personnalisée avec le public cible.... de clients: Encontrar un grupo de clientes con un comportamiento similar dada una gran base de donnéesUne base de données est un ensemble organisé d’informations qui vous permet de stocker, Gérez et récupérez efficacement les données. Utilisé dans diverses applications, Des systèmes d’entreprise aux plateformes en ligne, Les bases de données peuvent être relationnelles ou non relationnelles. Une bonne conception est essentielle pour optimiser les performances et garantir l’intégrité de l’information, facilitant ainsi la prise de décision éclairée dans différents contextes.... de clients (un exemple pratique est donné en utilisant la segmentation de la clientèle bancaire)
2) Classification du trafic réseau: Regroupement des caractéristiques des sources de trafic. Les types de trafic peuvent être facilement classés à l'aide de clusters.
3) filtre anti-spam: Les données sont regroupées dans différentes sections (entête, expéditeur et contenu) et ensuite ils peuvent aider à classer lesquels d'entre eux sont des spams.
4)urbanisme: Regroupement des maisons selon leur situation géographique, valeur et type de maison.
Différents types d'algorithmes de clustering
1) Regroupement des bas K – Utilisation de cet algorithme, nous trions un ensemble de données donné sur un certain nombre de clusters prédéterminés ou « k » groupes.
2) Regroupement hiérarchique – Suit deux approches Divisive et Agglomérative.
Agglomerative considère chaque observation comme un seul groupe, puis regroupe des points de données similaires jusqu'à ce qu'ils fusionnent en un seul groupe et Divisive fonctionne juste devant..
3) Clustering significatif C flou – Le fonctionnement de l'algorithme FCM est presque similaire à l'algorithme de clustering k-means, la principale différence est que dans FCM, un point de données peut être placé dans plus d'un groupe.
4) Regroupement spatial basé sur la densité – Útil en las áreas de aplicación donde requerimos estructuras de grappeUn cluster est un ensemble d’entreprises et d’organisations interconnectées qui opèrent dans le même secteur ou la même zone géographique, et qui collaborent pour améliorer leur compétitivité. Ces regroupements permettent le partage des ressources, Connaissances et technologies, favoriser l’innovation et la croissance économique. Les grappes peuvent couvrir une variété d’industries, De la technologie à l’agriculture, et sont fondamentaux pour le développement régional et la création d’emplois.... no lineales, basé uniquement sur la densité.
À présent, ici dans cet article, nous nous concentrerons profondément sur l'algorithme de clustering k-means, explications théoriques du fonctionnement des k-means, avantages et inconvénients, et un problème de regroupement pratique résolu qui améliorera la compréhension théorique et vous donnera un aperçu approprié. comment fonctionne le clustering k-means.
Quoi il est k-demi CLuster?
La agrupación de K-Means es un algoritmo de Apprentissage non superviséL’apprentissage non supervisé est une technique d’apprentissage automatique qui permet aux modèles d’identifier des modèles et des structures dans des données sans étiquettes prédéfinies. Grâce à des algorithmes tels que les k-moyennes et l’analyse en composantes principales, Cette approche est utilisée dans une variété d’applications, comme la segmentation de la clientèle, Détection d’anomalies et compression de données. Sa capacité à révéler des informations cachées en fait un outil précieux dans le..., qui est utilisé pour regrouper l'ensemble de données non étiqueté en différents groupes / sous-ensembles.
Ahora debe estar preguntándose qué significa ‘k’ Oui ‘ça veut dire’ dans k-means clustering cela signifie ??
Laissant toutes vos hypothèses de côté ici, ‘k’ définit le nombre de groupes prédéfinis à créer dans le processus de regroupement, disons si k = 2, il y aura deux groupes, et pour k = 3, il y aura trois groupes et ainsi de suite. Comme c'est un algorithme basé sur le centroïde, ‘des médias’ dans le clustering k-means, il est lié au centroïde des points de données où chaque cluster est associé à un centroïde. Le concept d'un algorithme basé sur le centroïde sera expliqué dans l'explication de travail de k-means.
Principalement, l'algorithme de clustering k-means effectue deux tâches:
- Détermine la valeur la plus optimale pour K points centraux ou centroïdes grâce à un processus itératif.
- Mappez chaque point de données à son centre k le plus proche. Le cluster est créé avec des points de données proches du centre particulier k.
Comment fonctionne le clustering k-means?
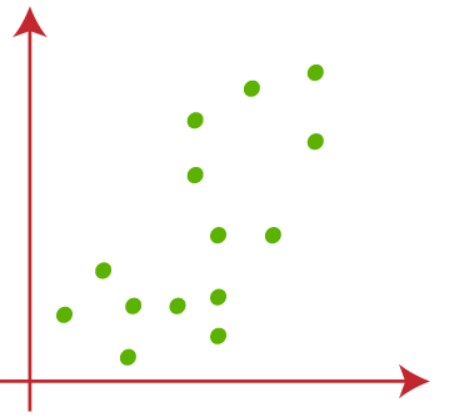
Supposons que nous ayons deux variables X1 et X2, Diagramme de dispersionLe nuage de points est un outil graphique utilisé en statistiques pour visualiser la relation entre deux variables. Il se compose d’un ensemble de points dans un plan cartésien, où chaque point représente une paire de valeurs correspondant aux variables analysées. Ce type de graphique vous permet d’identifier des modèles, Tendances et corrélations possibles, faciliter l’interprétation des données et la prise de décision sur la base des informations visuelles présentées.... ensuite:
(1) Supposons que la valeur de k, qui est le nombre de groupes prédéfinis, il est 2 (k = 2), donc ici nous allons regrouper nos données en 2 groupes.
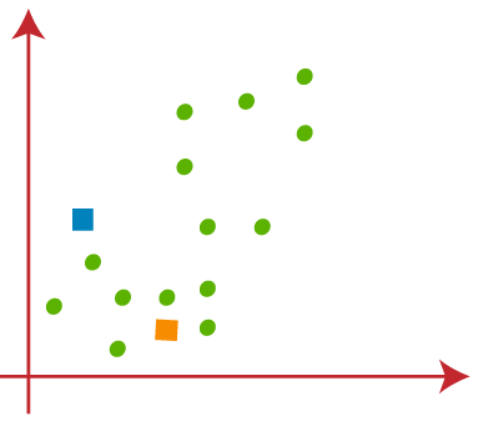
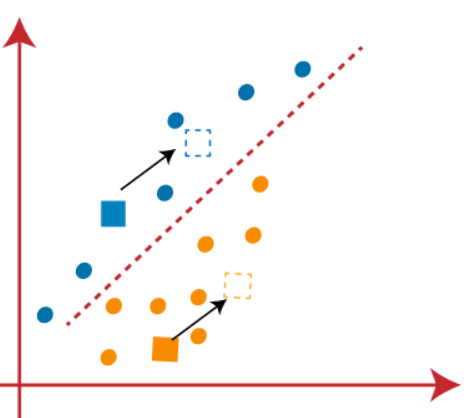
Il faut choisir k points au hasard pour former les groupes. Il ne peut y avoir aucune restriction sur la sélection de k points aléatoires à l'intérieur des données ou à l'extérieur.. Ensuite, ici nous envisageons 2 points comme k points (qui ne font pas partie de notre jeu de données) que se muestran en la siguiente chiffre"Chiffre" est un terme utilisé dans divers contextes, De l’art à l’anatomie. Dans le domaine artistique, fait référence à la représentation de formes humaines ou animales dans des sculptures et des peintures. En anatomie, désigne la forme et la structure du corps. En outre, en mathématiques, "chiffre" Il est lié aux formes géométriques. Sa polyvalence en fait un concept fondamental dans de multiples disciplines....:
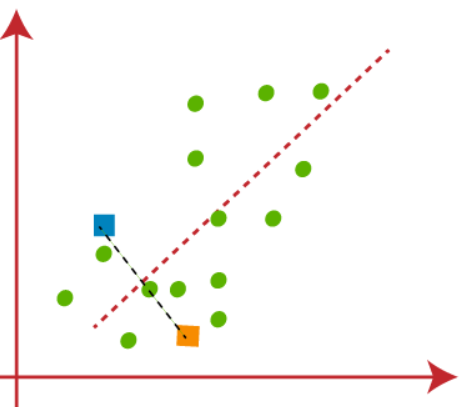
(2) L'étape suivante consiste à attribuer chaque point de données dans l'ensemble de données sur le nuage de points à son point k le plus proche, esto se hará calculando la distancia euclidiana entre cada punto con un punto k y dibujando una médianLa médiane est une mesure statistique qui représente la valeur centrale d’un ensemble de données ordonnées. Pour le calculer, Les données sont organisées de la plus basse à la plus élevée et le numéro au milieu est identifié. S’il y a un nombre pair d’observations, La moyenne des deux valeurs fondamentales est calculée. Cet indicateur est particulièrement utile dans les distributions asymétriques, puisqu’il n’est pas affecté par les valeurs extrêmes.... entre ambos centroides, montré dans la figure ci-dessous-
Nous pouvons clairement voir que le point à gauche de la ligne rouge est proche de K1 ou du barycentre bleu et les points à droite de la ligne rouge sont proches de K2 ou du barycentre orange..
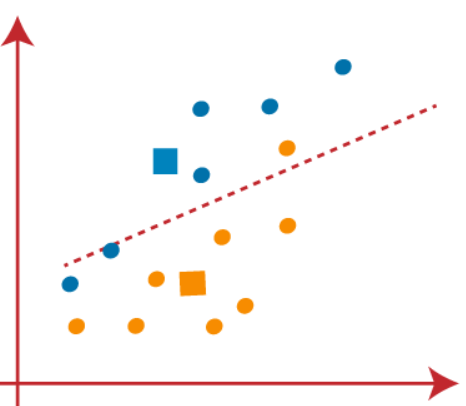
(3) Puisque nous devons trouver le point le plus proche, nous allons répéter le processus en choisissant un nouveau centroïde. Pour choisir les nouveaux centroïdes, nous allons calculer le centre de gravité de ces centroïdes et trouver de nouveaux centroïdes comme indiqué ci-dessous:
(4) À présent, nous devons remapper chaque point de données sur un nouveau centroïde. Pour cela, nous devons répéter le même processus de recherche d'une ligne médiane. La médiane sera comme ci-dessous:
Dans l'image ci-dessus, on peut voir, un point orange est sur le côté gauche de la ligne et deux points bleus sont juste à côté de la ligne. Ensuite, ces trois points seront affectés à de nouveaux barycentres
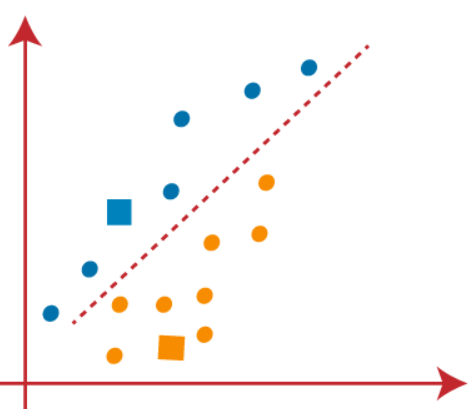
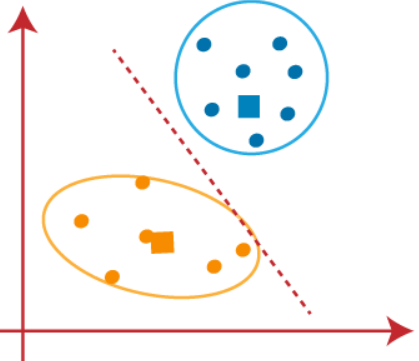
Nous continuerons à trouver de nouveaux centroïdes jusqu'à ce qu'il n'y ait plus de points différents des deux côtés de la ligne.
Nous pouvons maintenant supprimer les centroïdes supposés, et les deux derniers groupes seront comme indiqué dans l'image ci-dessous
Jusqu'à présent, nous avons vu comment fonctionne l'algorithme k-means et les différentes étapes nécessaires pour atteindre la destination finale des clusters de différenciation..
Maintenant tout le monde doit se demander comment choisir la valeur de k nombre de clusters.
El rendimiento del algoritmo de agrupación de K-means depende en gran mesureLa "mesure" C’est un concept fondamental dans diverses disciplines, qui fait référence au processus de quantification des caractéristiques ou des grandeurs d’objets, phénomènes ou situations. En mathématiques, Utilisé pour déterminer les longueurs, Surfaces et volumes, tandis qu’en sciences sociales, il peut faire référence à l’évaluation de variables qualitatives et quantitatives. La précision des mesures est cruciale pour obtenir des résultats fiables et valides dans toute recherche ou application pratique.... de las agrupaciones que forma. Choisir le nombre optimal de clusters est une tâche difficile. Il existe plusieurs façons de trouver le nombre optimal de clusters, mais ici nous discutons de deux méthodes pour trouver le nombre de clusters ou la valeur de K qui est le Méthode du coude et notation de la silhouette.
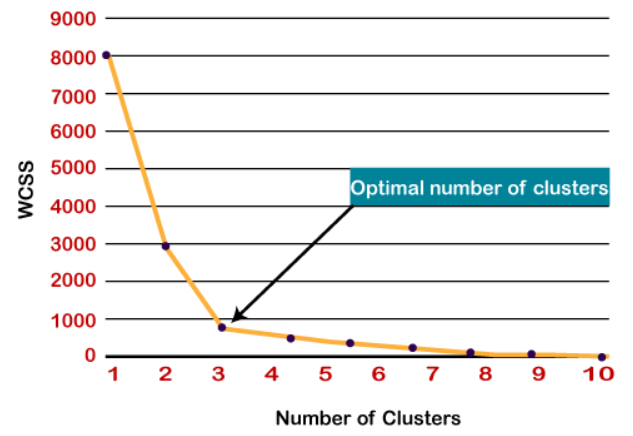
Método del codo para encontrar ‘k’ nombre de groupes:[1]
La méthode Elbow est la plus populaire pour trouver un nombre optimal de clusters., cette méthode utilise WCSS (Somme des carrés dans les clusters) représentant les variations totales au sein d'un cluster.
WCSS = ∑Pi et Cluster1 distance (Pje C1)2 + ??Pi et Cluster2distance (Pje C2)2+ ??Pi en CLuster3 distance (Pje C3)2
Dans la formule ci-dessus ∑Pi et Cluster1 distance (Pje C1)2 est la somme du carré des distances entre chaque point de données et son centre de gravité dans un groupe1 de même pour les deux autres termes de la formule ci-dessus.
Étapes impliquées dans la méthode du coude:
- K- signifie que le clustering est fait pour différentes valeurs de k (de 1 une 10).
- Le WCSS est calculé pour chaque groupe.
- Une courbe est tracée entre les valeurs WCSS et le nombre de clusters k.
- Le point de courbure aigu ou un point de tracé ressemble à un bras, alors ce point est considéré comme la meilleure valeur de K.
Alors ici, comme nous pouvons le voir, une courbe raide est à k = 3, donc le nombre optimal de groupes est 3.
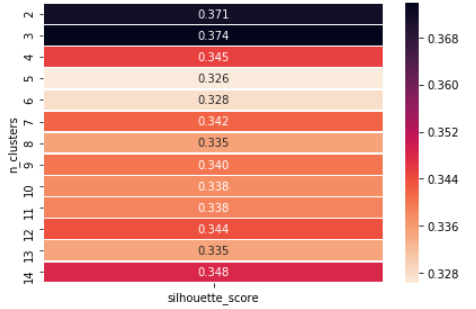
ponctuation des silhouettes Método para encontrar ‘k’ nombre de grappes
La valeur de la silhouette est une mesure de la similarité d'un objet avec son propre groupe (cohésion) par rapport aux autres groupes (séparation). La silhouette varie de -1 une +1, où une valeur élevée indique que l'objet correspond bien à son propre groupe et non aux groupes voisins. Si la plupart des objets ont une valeur élevée, alors la configuration de regroupement est appropriée. Si de nombreux points ont une valeur faible ou négative, alors la configuration de clustering peut avoir trop ou trop peu de clusters.
Ejemplo que muestra cómo podemos elegir el valor de ‘k’, puisque nous pouvons voir qu'en n = 3 nous avons le score maximum de silhouette, donc, on choisit la valeur de k = 3.
Avantages de l'utilisation du clustering k-means
- Facile à mettre en œuvre.
- Avec beaucoup de variables, K-Means peut être plus rapide en termes de calcul que le clustering hiérarchique (si K est petit).
- k-means peut produire des clusters plus élevés que les clusters hiérarchiques.
Inconvénients de l'utilisation du clustering k-means
Il est difficile de prédire le nombre de clusters (Valeur K).
Les graines initiales ont un fort impact sur les résultats finaux.
Implémentation pratique de l'algorithme de clustering K-means en utilisant Python (segmentation de la clientèle bancaire)
Ici, nous importons les bibliothèques nécessaires à notre analyse.
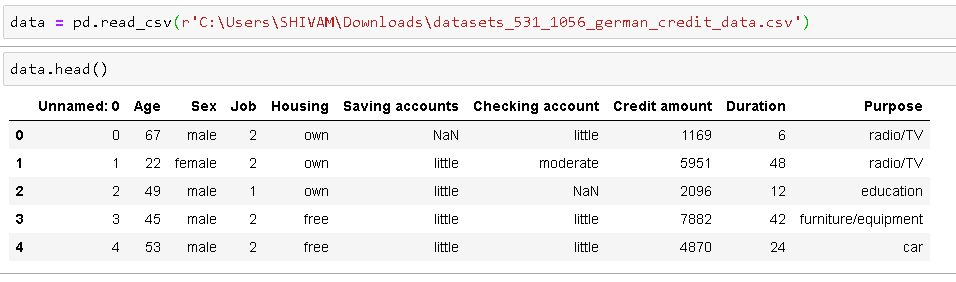
Lire les données et obtenir le 5 meilleures observations pour examiner l'ensemble de données
Code pour EDA non inclus (L'analyse exploratoire des données), L'EDA a été réalisée sur ces données et une analyse des valeurs aberrantes a été réalisée pour nettoyer les données et les rendre adaptées à notre analyse..
Comme nous savons, Les K-moyennes sont effectuées uniquement sur des données numériques, nous choisissons donc les colonnes numériques pour notre analyse.
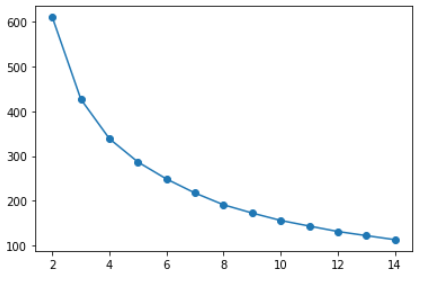
À présent, pour effectuer le clustering k-means comme indiqué précédemment dans cet article, necesitamos encontrar el valor del número ‘k’ de groupements et nous pouvons le faire en utilisant le code suivant, ici, nous utilisons différentes valeurs de k pour le regroupement, puis la sélection à l'aide de la Méthode du coude.
Lorsque le nombre de grappes augmente, l'écart (somme des carrés dans le cluster) diminue. le coude dans 3 O 4 groupes représente le compromis le plus parcimonieux entre la minimisation du nombre de groupes et la minimisation de la variance au sein de chaque groupe, nous pouvons donc choisir une valeur de k pour être 3 O 4
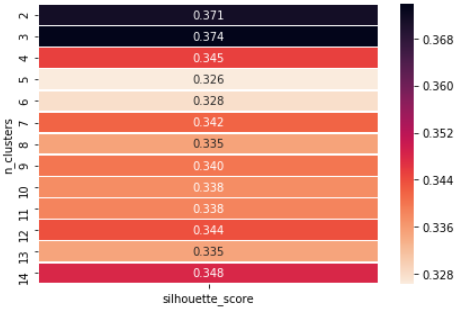
Ahora se muestra cómo podemos usar el método del valor de silueta para encontrar el valor de ‘k’.
Si nous observons, nous obtenons le nombre optimal de clusters à n = 3, donc finalement on peut choisir la valeur de k = 3.
À présent, ajuster l'algorithme pour k signifie utiliser la valeur de k = 3 y trazar el carte de chaleurUn "carte de chaleur" est une représentation graphique qui utilise des couleurs pour montrer la densité des données dans une zone spécifique. Couramment utilisé dans l’analyse de données, Etudes marketing et comportementales, Ce type de visualisation vous permet d’identifier rapidement les modèles et les tendances. Par des variations chromatiques, Les cartes thermiques facilitent l’interprétation de grands volumes d’informations, aider à prendre des décisions éclairées.... para los clústeres.
analyse finale
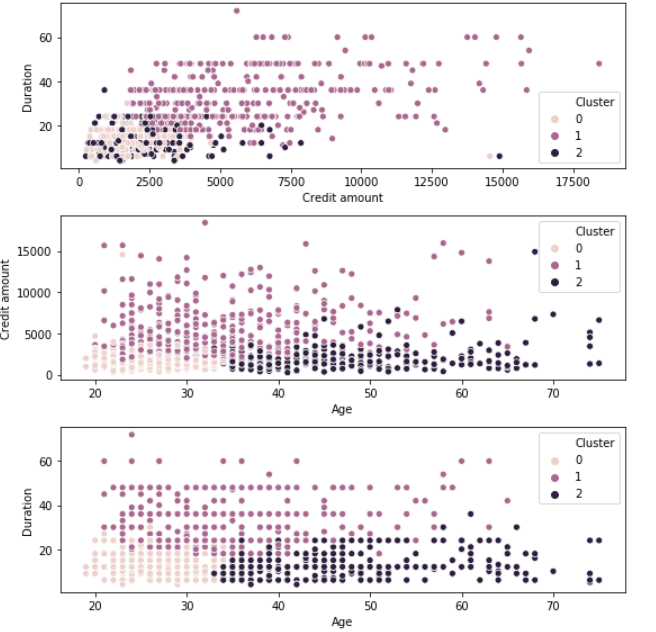
groupe 0: jeunes clients souscrivant des prêts à faible crédit pour une courte période
Grouper 1: Clients d'âge moyen qui contractent des prêts à crédit élevé sur une longue période
Grouper 2: Clients âgés qui obtiennent des prêts de crédit moyen pour une courte période
conclusion
Nous avons discuté de ce qu'est le clustering, leurs types et leur application dans différentes industries. Nous discutons de ce qu'est le clustering k-means, comment fonctionne l'algorithme de clustering k-means, dos métodos para seleccionar el número ‘k’ de groupements, et ses avantages et inconvénients. Alors, nous sommes passés par la mise en œuvre pratique de l'algorithme de clustering k-means en utilisant le problème de segmentation de la clientèle bancaire en Python.
Les références:
(1) img (1) une image (8) Oui [1] , référence tirée de « Algorithme de clustering K-means »
https://www.javatpoint.com/k-means-clustering-algorithm-in-machine-learning
En rapport
Articles Similaires:
- K signifie regroupement | K signifie algorithme de clustering en machine learning
- Regroupement des bas K | K-means clustering avec R pour les data scientists
- Regroupement en R | Guide du débutant sur le clustering dans R
- Le moniteur n'écrit pas de signal, Aucun signal détecté, Vérifiez le câble de signal, Qu'est-ce que cela signifie et que dois-je faire?