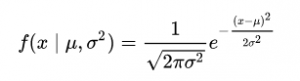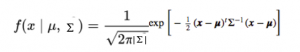Algorithme de maximisation des attentes | Explication de l'algorithme EM

Cet article a été publié dans le cadre du Blogathon sur la science des données

introduction

sont observables. Puisque nous n'avons pas les valeurs pour les variables non observées (latent), la Attente-Maximisation El algoritmo intenta utilizar los datos existentes para determinar los valores óptimos para estas variables y luego encuentra los paramètresLes "paramètres" sont des variables ou des critères qui sont utilisés pour définir, mesurer ou évaluer un phénomène ou un système. Dans divers domaines tels que les statistiques, Informatique et recherche scientifique, Les paramètres sont essentiels à l’établissement de normes et de standards qui guident l’analyse et l’interprétation des données. Leur sélection et leur manipulation correctes sont cruciales pour obtenir des résultats précis et pertinents dans toute étude ou projet.... del modelo.

Table des matières

• ?? Quel est l'algorithme de maximisation des attentes (DANS)?
• ?? Explication détaillée de l'algorithme EM
• ?? Diagramme de flux
• Avantages et inconvénients
• Applications de l'algorithme EM
• 👉 Cas d'utilisation de l'algorithme EM
  • Introduction aux distributions gaussiennes
  • Modèles de mélange gaussien (GMM)
• Implémentation de modèles de mélanges gaussiens en Python

Quel est l'algorithme de maximisation des attentes (DANS)?

👉 Es un modelo de variableEn statistique et en mathématiques, ongle "variable" est un symbole qui représente une valeur qui peut changer ou varier. Il existe différents types de variables, et qualitatif, qui décrivent des caractéristiques non numériques, et quantitatif, représentation de grandeurs numériques. Les variables sont fondamentales dans les expériences et les études, puisqu’ils permettent l’analyse des relations et des modèles entre différents éléments, faciliter la compréhension de phénomènes complexes.... latente.

Premier, Comprenons ce que l'on entend par modèle à variable latente.

Un modèle à variables latentes consiste en observable variables avec inobservable variables. Les variables observées sont les variables de l'ensemble de données qui peuvent être mesurées, tandis que les variables non observées (latent / caché) sont déduits des variables observées.

• 👉 Peut être utilisé pour trouver maximum de vraisemblance local (MLE) paramètres ou maximum a posteriori (CARTE) paramètres pour les variables latentes
  dans un modèle statistique ou mathématique.
• 👉 Utilisé pour prédire ces valeurs manquantes dans l'ensemble de données, à condition de connaître la forme générale de la distribution de probabilité associée à ces variables latentes.
• En termes simples, l'idée de base derrière cet algorithme est d'utiliser les échantillons observables de variables latentes pour prédire les valeurs d'échantillons qui ne sont pas observables pour l'apprentissage. Ce processus est répété jusqu'à ce que la convergence des valeurs se produise.

Explication détaillée de l'algorithme EM

?? Voici l'algorithme que vous devez suivre:

• Étant donné un ensemble de données incomplet, commencer avec un ensemble de paramètres initialisés.
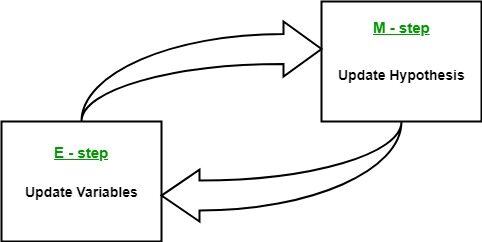
• Étape d'attente (étape E): Dans cette étape d'attente, en utilisant les données observées disponibles à partir de l'ensemble de données, nous pouvons essayer d'estimer ou de deviner les valeurs de données manquantes. Finalement, après cette étape, nous obtenons des données complètes sans valeurs manquantes.
• Étape de maximisation (étape M): À présent, nous devons utiliser toutes les données, qui se préparent dans l'étape d'attente, et mettre à jour les paramètres.
• Répéter l'étape 2 et le pas 3 jusqu'à ce que nous convergeons vers notre solution.

Source de l'image: Relier

??

Objectif de l'algorithme de maximisation des attentes

L'algorithme de maximisation des attentes vise à utiliser les données observées disponibles à partir de l'ensemble de données pour estimer les données manquantes pour les variables latentes, puis à utiliser ces données pour mettre à jour les valeurs des paramètres dans l'étape de maximisation..

Comprenons l'algorithme EM en détail:

• jeÉtape d'initialisation: Dans cette étape, on initialise les valeurs des paramètres avec un ensemble de valeurs initiales, puis nous livrons l'ensemble de données observé incomplet au système en supposant que les données observées proviennent d'un modèle spécifique. c'est-à-dire, distribution de probabilité.
• Étape d'attente: Dans cette étape, utiliser les données observées pour estimer ou deviner les valeurs de données manquantes ou incomplètes. Utilisé pour mettre à jour les variables.
• Étape de maximisation: Dans cette étape, nous utilisons les données complètes générées dans le “Attente” étape pour mettre à jour les valeurs des paramètres, c'est-à-dire, mettre à jour l'hypothèse.
• Vérification de la convergence Étape: À présent, dans cette étape, on vérifie si les valeurs convergent ou non, si c'est ainsi, Arrêter, sinon répétez ces deux étapes, c'est-à-dire, les “Attente” étape et “Maximisation” étape jusqu'à ce que la convergence se produise.

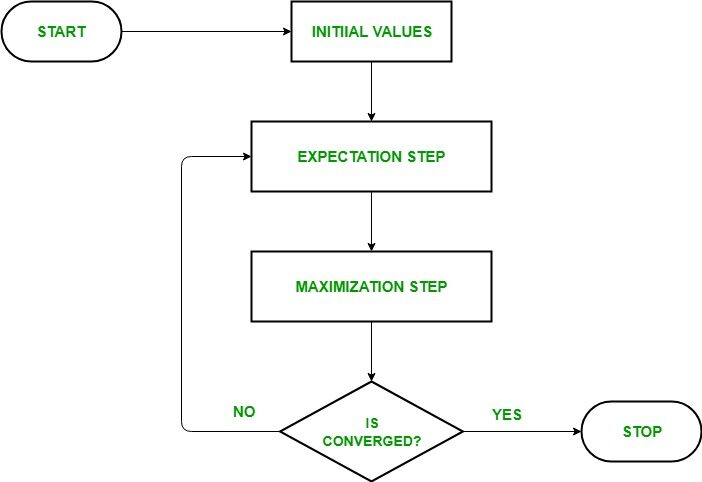
Organigramme de l'algorithme EM

Source de l'image: Relier

Avantages et inconvénients de l'algorithme EM

?? avantage

• Les deux étapes de base de l'algorithme EM, c'est-à-dire, E-étape et M-étape, sont généralement assez faciles pour de nombreux problèmes d'apprentissage automatique en termes de mise en œuvre.
• La solution aux étapes M existe souvent sous forme fermée.
• La valeur de probabilité est toujours garantie d'augmenter après chaque itération.

?? Désavantages

• Possède convergence lente.
• Converger vers le optimum local seulement.
• Il prend en compte à la fois les probabilités avant et arrière. Ceci contraste avec l'optimisation numérique qui ne considère que chances d'avance.

Applications de l'algorithme EM

Le modèle de variable latente a plusieurs applications réelles dans l'apprentissage automatique:

• Utilisé pour calculer le Densité gaussienne d'une fonction.
• Utile pour compléter le données perdues lors d'un spectacle.
• Trouve beaucoup d'utilisation dans différents domaines comme Traitement du langage naturel (PNL), Vision par ordinateur, etc.
• Utilisé dans la reconstruction d'images dans le domaine de Médecine et génie des structures.
• Il est utilisé pour estimer les paramètres du Modèle de Markov caché (HMM) et aussi pour certains autres modèles mixtes comme mélange gaussien Des modèlesetc.
• Il est utilisé pour trouver les valeurs des variables latentes.

Cas d'utilisation de l'algorithme EM

Notions de base sur la distribution gaussienne

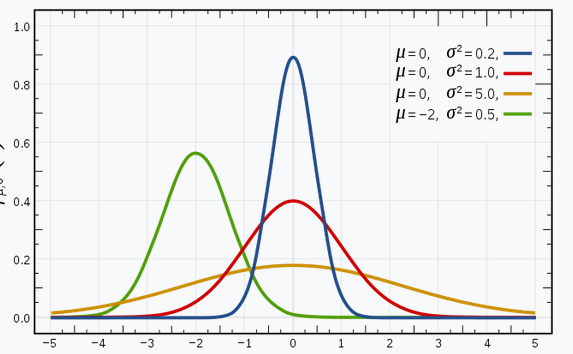
Je suis sûr que vous connaissez les distributions gaussiennes (ou la distribution normale), car cette distribution est beaucoup utilisée dans le domaine de l'apprentissage automatique et des statistiques. A une courbe en forme de cloche, avec les observations distribuées symétriquement autour de la valeur moyenne (moyenne).

L'image donnée a des distributions gaussiennes avec différentes valeurs de la moyenne (??) et l'écart (??²). Rappelez-vous que plus la valeur de est grande (écart-type), plus l'extension le long de l'axe est grande.

Source de l'image: Relier

Dans l'espace 1D, les fonction de densité de probabilité d'une distribution gaussienne est donnée par:

Figure. Fonction de densité de probabilité (PDF)

où représente la moyenne et σ² représente l'écart.

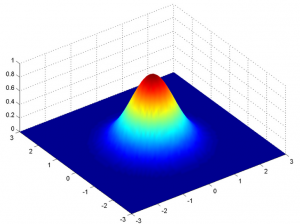
Mais cela ne serait vrai que pour une variable en 1-D uniquement. Dans le cas de deux variables, nous aurons une courbe en cloche 3D au lieu d'une courbe en forme de cloche 2D comme indiqué ci-dessous:

La fonction de densité de probabilité serait donnée par:

où x est le vecteur d'entrée, μ est le vecteur moyen 2-D et Σ est la matrice de covariance 2 × 2. Podemos generalizar lo mismo para la dimension"Dimension" C’est un terme qui est utilisé dans diverses disciplines, comme la physique, Mathématiques et philosophie. Il s’agit de la mesure dans laquelle un objet ou un phénomène peut être analysé ou décrit. En physique, par exemple, On parle de dimensions spatiales et temporelles, alors qu’en mathématiques, il peut faire référence au nombre de coordonnées nécessaires pour représenter un espace. Sa compréhension est fondamentale pour l’étude et... ré.

Donc, pour le modèle gaussien multivarié, on a x et comme vecteurs de longueur d, et serait un dxd Matrice de covariance.

Donc, pour un ensemble de données qui a ré fonctionnalités, nous aurions un mélange de k Distributions gaussiennes (où k représente le nombre de clusters), chacun avec un vecteur moyen et une matrice de variance déterminés.

Mais notre question est: “Comment pouvons-nous trouver la moyenne et la variance de chaque gaussienne?”

Pour trouver ces valeurs, nous utilisons une technique appelée Espérance-Maximisation (DANS).

Modèles de mélange gaussien

L'hypothèse principale de ces modèles de mélange est qu'il existe un certain nombre de distributions gaussiennes, et chacune de ces distributions représente un groupe. Donc, un modèle de mélange gaussien tente de regrouper les observations qui appartiennent à une seule distribution.

Los modelos de mezcla gaussianos son modelos probabilísticos que utilizan el enfoque de regroupementLe "regroupement" Il s’agit d’un concept qui fait référence à l’organisation d’éléments ou d’individus en groupes ayant des caractéristiques ou des objectifs communs. Ce procédé est utilisé dans diverses disciplines, y compris la psychologie, Éducation et biologie, faciliter l’analyse et la compréhension de comportements ou de phénomènes. Dans le domaine de l’éducation, par exemple, Le regroupement peut améliorer l’interaction et l’apprentissage entre les élèves en encourageant le travail.. suave para distribuir las observaciones en diferentes grupos, c'est-à-dire, différentes distributions gaussiennes.

Par exemple, le modèle de mélange gaussien de 2 Distributions gaussiennes

On a deux distributions gaussiennes: N (??₁, ??₁²) et n(??₂, ??₂²)

Ici, nous devons estimer un total de 5 paramètres:

= (p, ??₁, ??₁²,??₂, ??₂²)

où p est la probabilité que les données proviennent de la première distribution gaussienne et 1-p qu'elles proviennent de la deuxième distribution gaussienne.

Ensuite, la fonction de densité de probabilité (PDF) du modèle de mélange est donnée par:

g (X |??) = p₁(X | ??₁, ??₁²) + (1-p) g₂(X | ??₂, ??₂² )

Cibler: Pour mieux ajuster une densité de probabilité donnée en trouvant = (p, ??₁, ??₁², ??₂, ??₂²) via des itérations EM.

Implémentation GMM en Python

Il est temps de plonger dans le code! Ici pour la mise en œuvre, nous utilisons le Bibliothèque Sklearn de Python.

De sklearn, nous utilisons la classe GaussianMixture qui implémente l'algorithme EM pour ajuster un mélange de modèles gaussiens. Après la création de l'objet, en utilisant le Mélange gaussien.fit método podemos aprender un modelo de mezcla gaussiana a partir de los datos de entraînementLa formation est un processus systématique conçu pour améliorer les compétences, connaissances ou aptitudes physiques. Il est appliqué dans divers domaines, Comme le sport, Éducation et développement professionnel. Un programme d’entraînement efficace comprend la planification des objectifs, Pratique régulière et évaluation des progrès. L’adaptation aux besoins individuels et la motivation sont des facteurs clés pour obtenir des résultats réussis et durables dans toutes les disciplines.....

Paso 1: Importez les packages nécessaires

importer numpy en tant que np
importer matplotlib.pyplot en tant que plt
de sklearn.mixture importer GaussianMixture

Paso 2: créer un objet de la classe Mélange gaussien

gmm = mélange gaussien(n_composants = 2, péage=0.000001)

Paso 3: adapte l'objet créé à un ensemble de données donné

gmm.fit(np.expand_dims(Les données, 1))

Paso 4: Paramètres d'impression de 2 gaussiennes entrantes

Gaussienne_nr = 1
imprimer('Entrée Normal_distb {:}: = {:.2}, = {:.2}'.format("1", Moyenne1, Standard_dev1))
imprimer('Entrée Normal_distb {:}: = {:.2}, = {:.2}'.format("2", Moyenne2, Standard_dev2))

Sortir:

Entrée Normal_distb 1: = 2.0, = 4.0

Entrée Normal_distb 2: = 9.0, = 2.0

Paso 5: Paramètres d'impression après mélange 2 gaussianos

pour mu, Dakota du Sud, p en zip(gmm.means_.flatten(), np.sqrt(gmm.covariances_.flatten()), gmm.poids_):
    imprimer('Normal_distb {:}: = {:.2}, = {:.2}, poids = {:.2}'.format(Gaussienne_nr, mu, Dakota du Sud, p))
    g_s = stats.norm(mu, Dakota du Sud).pdf(X) * p
    plt.plot(X, g_s, étiquette="sklearn gaussien");
    Gaussienne_nr += 1

Production:

Normal_distb 1: = 1,7, = 3,8, poids = 0,61

Normal_distb 2: = 8.8, = 2.2, poids = 0.39

Paso 6: Tracer les parcelles de distribution

sns.distplot(Les données, bacs=20, kde = Faux, norm_hist=Vrai)
gmm_sum = np.exp([gmm.score_samples(e.remodeler(-1, 1)) pour e dans x]) 
plt.plot(X, gmm_sum, étiquette="mélange gaussien");
plt.légende();

Production:

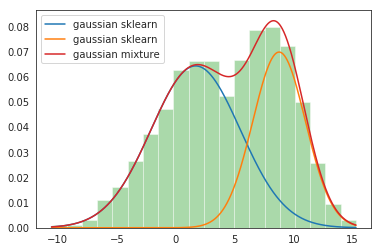
Ceci termine notre implémentation GMM !!

Remarques finales

Merci pour la lecture!

Si vous avez aimé cela et que vous voulez en savoir plus, visitez mes autres articles sur la science des données et l'apprentissage automatique en cliquant sur le Relier

N'hésitez pas à me contacter au Linkedin, Courrier électronique.

Tout ce qui n'est pas mentionné ou voulez-vous partager vos pensées? N'hésitez pas à commenter ci-dessous et je vous répondrai.

A propos de l'auteur

Chirag Goyal

Actuellement, Je poursuis mon Bachelor of Technology (B.Tech) en informatique et ingénierie de Institut indien de technologie Jodhpur (IITJ). Je suis très enthousiasmé par l'apprentissage automatique, les l'apprentissage en profondeurL'apprentissage en profondeur, Une sous-discipline de l’intelligence artificielle, s’appuie sur des réseaux de neurones artificiels pour analyser et traiter de grands volumes de données. Cette technique permet aux machines d’apprendre des motifs et d’effectuer des tâches complexes, comme la reconnaissance vocale et la vision par ordinateur. Sa capacité à s’améliorer continuellement au fur et à mesure que de nouvelles données lui sont fournies en fait un outil clé dans diverses industries, de la santé... y la inteligencia artificial.

Les médias présentés dans cet article sur Algorithme de maximisation des attentes ne sont pas la propriété de DataPeaker et sont utilisés à la discrétion de l'auteur.

En rapport