Algoritmo de regressão linear para fácil previsão

Este artigo foi publicado como parte do Data Science Blogathon

Introdução

. Un problema de regresión es cuando la variávelEm estatística e matemática, uma "variável" é um símbolo que representa um valor que pode mudar ou variar. Existem diferentes tipos de variáveis, e qualitativo, que descrevem características não numéricas, e quantitativo, representando quantidades numéricas. Variáveis são fundamentais em experimentos e estudos, uma vez que permitem a análise de relações e padrões entre diferentes elementos, facilitando a compreensão de fenômenos complexos.... de salida es un valor real o continuo.

Em regressão, nós traçamos um gráfico entre as variáveis ​​que melhor se ajustam aos pontos de dados fornecidos. O modelo de aprendizado de máquina pode fornecer previsões sobre os dados. Aqui estão algumas dicas grátis!, “A regressão exibe uma linha ou curva que passa por todos os pontos de dados em um gráfico de previsão de destino de tal forma que a distância vertical entre os pontos de dados e a linha de regressão seja mínima”. É usado principalmente para prever, prever, modelar séries temporais e determinar a relação causal-efeito entre as variáveis.

Tipos de modelos de regressão

1. Regressão linear
2. Regressão polinomial
3. Regressão logística

Regressão linear

A regressão linear é um método de regressão estatística simples e silencioso usado para análise preditiva e mostra a relação entre variáveis ​​contínuas. A regressão linear mostra a relação linear entre a variável independente (Eixo X) e a variável dependente (Eixo y), conseqüentemente chamado de regressão linear. Se houver uma única variável de entrada (x), a referida regressão linear é chamada Regressão linear simples. E se houver mais de uma variável de entrada, a referida regressão linear é chamada Regressão linear múltipla. O modelo de regressão linear fornece uma linha reta inclinada que descreve a relação dentro das variáveis.

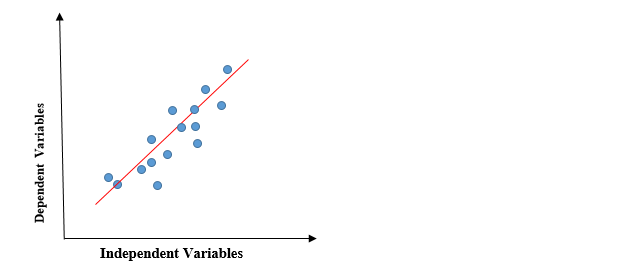
O gráfico anterior apresenta a relação linear entre a variável dependente e as variáveis ​​independentes. Quando o valor de x (variável independente) aumenta, o valor de y (variável dependente) também está aumentando. A linha vermelha é conhecida como a linha reta de melhor ajuste.. Com base nos pontos de dados fornecidos, tentamos traçar uma linha que modele melhor os pontos.

Para calcular a regressão linear da linha de melhor ajuste, uma forma tradicional de interceptação de declive é usada.

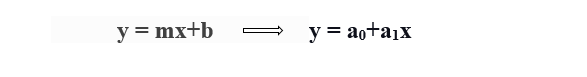
y = variável dependente.

x = variável independente.

a0 = intersecção da linha.

a1 = Coeficiente de regressão linear.

Necessidade de uma regressão linear

Como mencionado anteriormente, a regressão linear estima a relação entre uma variável dependente e uma variável independente. Vamos entender isso com um exemplo simples:

Digamos que desejamos estimar o salário de um funcionário com base no ano de experiência. Você tem os dados recentes da empresa, o que indica que a relação entre experiência e salário. Aqui, o ano de experiência é uma variável independente e o salário do funcionário é uma variável dependente., uma vez que o salário de um funcionário depende da experiência do funcionário. Com esta informação, podemos prever o futuro salário do funcionário com base nas informações atuais e passadas.

Uma linha de regressão pode ser uma relação linear positiva ou uma relação linear negativa.

Relação linear positiva

Se a variável dependente se expande no eixo Y e a variável independente progride no eixo X, esta relação é chamada de relação linear positiva.

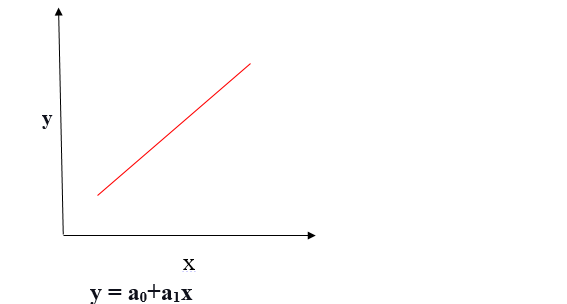
Relação linear negativa

Se a variável dependente diminui no eixo Y e a variável independente aumenta no eixo X, esta relação é chamada de relação linear negativa.

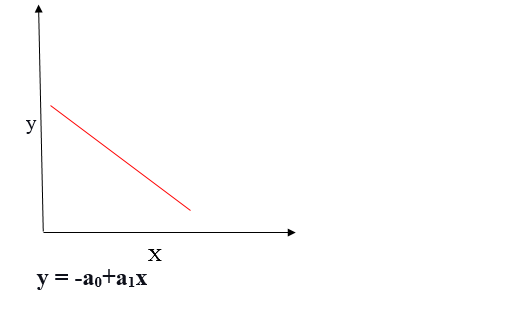
O objetivo do algoritmo de regressão linear é obter os melhores valores para a0 e a1 para encontrar a linha de melhor ajuste. A linha de melhor ajuste deve ter o menor erro, o que significa que o erro entre os valores previstos e os valores reais deve ser minimizado.

Função de custo

A função de custo ajuda a determinar os melhores valores possíveis para a0 e a1, que fornece a linha de melhor ajuste para os pontos de dados.

A função de custo otimiza os coeficientes ou pesos de regressão e mede o desempenho de um modelo de regressão linear. A função de custo é usada para encontrar a precisão do função de mapeamento que mapeia a variável de entrada para a variável de saída. Esta função de mapeamento também é conhecida como a função de hipótese.

Em regressão linear, Raiz do erro quadrático médio (MSE) A função de custo é usada, que é a média do erro quadrático que ocorreu entre os valores previstos e os valores reais.

Pela equação linear simples y = mx + b podemos calcular MSE como:

Vamos y = valores reais, e_eu = valores preditos

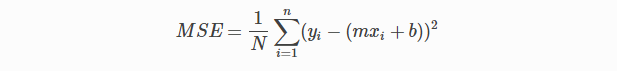
Usando a função MSE, vamos alterar os valores de a0 e a1 para que o valor MSE seja definido para os mínimos. Parâmetroso "parametros" são variáveis ou critérios usados para definir, medir ou avaliar um fenômeno ou sistema. Em vários domínios, como a estatística, Ciência da Computação e Pesquisa Científica, Os parâmetros são essenciais para estabelecer normas e padrões que orientam a análise e interpretação dos dados. Sua seleção e manuseio adequados são cruciais para obter resultados precisos e relevantes em qualquer estudo ou projeto.... del modelo XI, b (uma₀,uma₁) pode ser manipulado para minimizar a função de custo. Esses parâmetros podem ser determinados usando o método de gradiente descendente para que o valor da função de custo seja mínimo.

Gradiente descendente

O gradiente descendente é um método de atualizar a0 e a1 para minimizar a função de custo (MSE). Um modelo de regressão usa gradiente descendente para atualizar os coeficientes da linha (a0, a1 => XI, b) reduzindo a função de custo usando uma seleção aleatória de valores de coeficiente e, em seguida, atualizando iterativamente os valores para alcançar a função de custo mínimo.

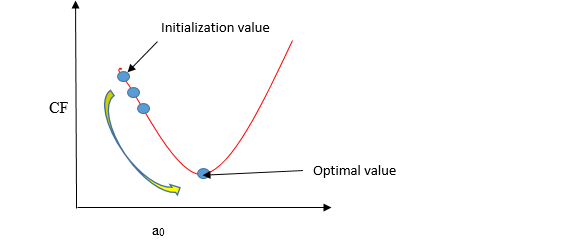
Imagine um poço em forma de U. Você está no ponto mais alto do poço e seu objetivo é chegar ao fundo do poço. Existe um tesouro, e você só pode seguir um número discreto de etapas para chegar ao fundo. Se você decidir dar um passo de cada vez, você eventualmente alcançará o fundo do poço, mas isso vai demorar mais. Se você optar por dar passos mais longos a cada vez, pode chegar mais cedo, mas existe a possibilidade de passar pelo fundo do poço e não perto do fundo. No algoritmo de descida gradiente, o número de passos que você dá é a taxa de aprendizagem, e isso decide o quão rápido o algoritmo converge para os mínimos.

Para atualizar um₀ e um₁, pegamos gradientes da função de custo. Para encontrar esses gradientes, tomamos derivadas parciais para um₀ e um₁.

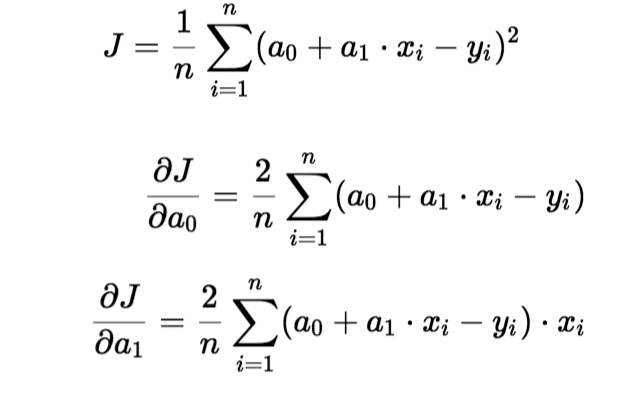
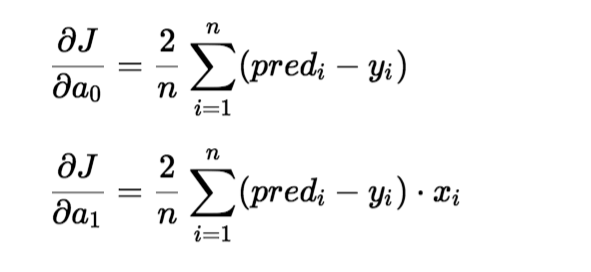
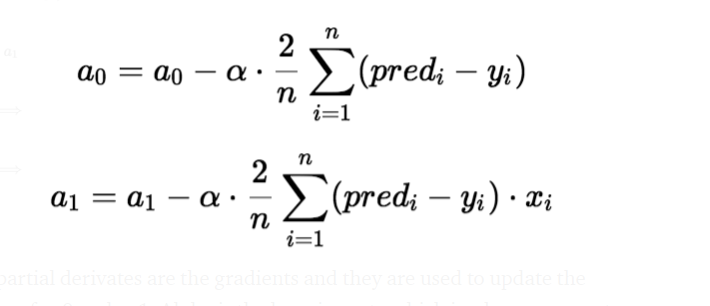
As derivadas parciais são os gradientes e são usadas para atualizar os valores de um₀ e um₁. Alpha é a taxa de aprendizagem.

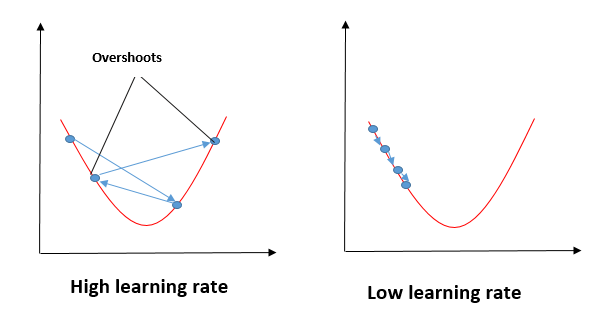
Impacto de diferentes valores para a taxa de aprendizagem

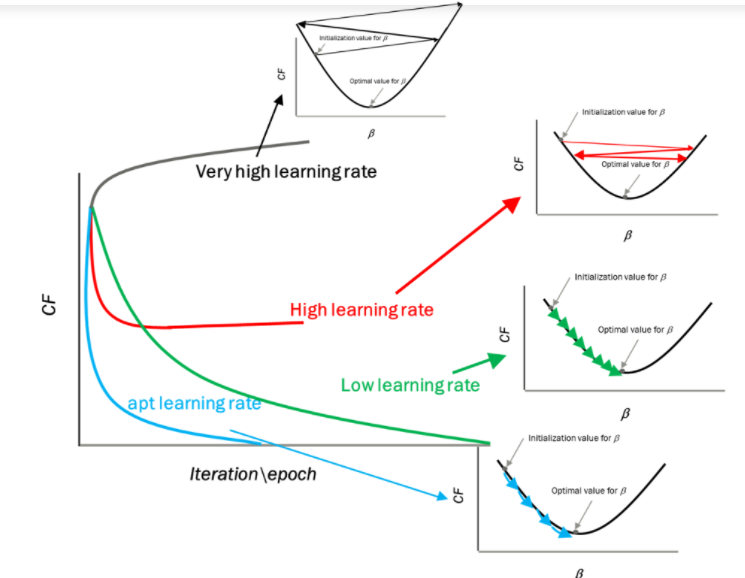
Fonte: mygreatleaning.com

A linha azul representa o valor ideal da taxa de aprendizagem e o valor da função de custo é minimizado em algumas iterações. A linha verde representa se a taxa de aprendizagem é menor que o valor ideal, então o número de iterações necessárias é alto para minimizar a função de custo. Se a taxa de aprendizagem selecionada for muito alta, a função de custo pode continuar a aumentar com iterações e saturar para um valor superior ao valor mínimo, aquele representado por uma linha vermelha e preta.

Caso de uso

Nisto, Vou pegar números aleatórios para a variável dependente (salário) e uma variável independente (experiência) e vou prever o impacto de um ano de experiência no salário.

Etapas para implementar o modelo de regressão linear

importar algumas bibliotecas necessárias

import matplotlib.pyplot as plt
import pandas as pd
import numpy as np

Defina o conjunto de dados

x= np.array([2.4,5.0,1.5,3.8,8.7,3.6,1.2,8.1,2.5,5,1.6,1.6,2.4,3.9,5.4])
y = np.array([2.1,4.7,1.7,3.6,8.7,3.2,1.0,8.0,2.4,6,1.1,1.3,2.4,3.9,4.8])
n = np.size(x)

Plote os pontos de dados

plt.scatter(experiência,salário, color ="vermelho")
plt.xlabel("Experiência")
plt.ylabel("Salário")
plt.show()

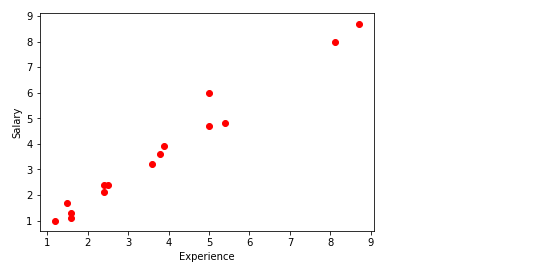
A principal função para calcular valores de coeficiente.

1. Parâmetros de inicialização.
2. Prever o valor de uma variável dependente dada uma variável independente.
3. Calcule o erro na previsão para todos os pontos de dados.
4. Calcule a derivada parcial wrt a0 e a1.
5. Calcule o custo de cada número e adicione-os.
6. Atualize os valores de a0 e a1.

#initialize the parameters
a0 = 0                  #intercept
a1 = 0                  #Slop
lr = 0.0001             #Learning rate
iterations = 1000       # Number of iterations
error = []              # Conjunto de erros para calcular o custo de cada iteração.
para itr em alcance(Iterações):
    error_cost = 0
    cost_a0 = 0
    cost_a1 = 0
    para eu no alcance(len(experiência)):
        y_pred = a0+a1 *experiência[eu]   # predict value for given x
        error_cost = error_cost +(salário[eu]-y_pred)**2
        para j no intervalo(len(experiência)):
            partial_wrt_a0 = -2 *(salário[j] - (a0 + a1 *experiência[j]))                #partial derivative w.r.t a0
            partial_wrt_a1 = (-2*experiência[j])*(salário[j]-(a0 + a1 *experiência[j]))   #partial derivative w.r.t a1
            cost_a0 = cost_a0 + partial_wrt_a0      #calculate cost for each number and add
            cost_a1 = cost_a1 + partial_wrt_a1      #calculate cost for each number and add
        a0 = a0 - lr * cost_a0    #update a0
        a1 = a1 - lr * cost_a1    #update a1
        print(itr,a0,a1)          #Check iteration and updated a0 and a1
    error.append(error_cost)      #Anexar os dados no array

En una iteración aproximada de 50-60, obtuvimos el valor de a0 y a1.

imprimir(a0)
imprimir(a1)

Trazar el erro para cada iteración.

plt.figure(figsize =(10,5))
plt.plot(np.arange(1,len(erro)+1),erro,color ="vermelho",largura de linha = 5)
plt.title("Erro de realidade virtual de iteração")
plt.xlabel("Iterações")
plt.ylabel("Erro")

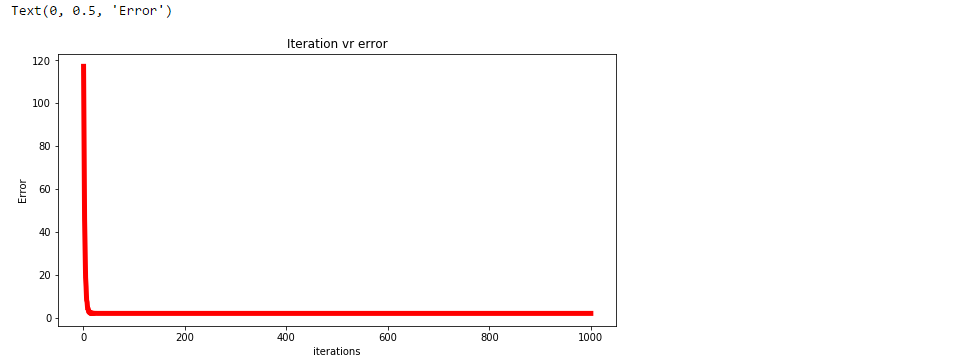
Prever valores.

pred = a0+a1*experience
print(pred)

Rastreie a linha de regressão.

plt.scatter(experiência,salário,color ="vermelho")
plt.plot(experiência,pred, color ="verde")
plt.xlabel("experiência")
plt.ylabel("salário")

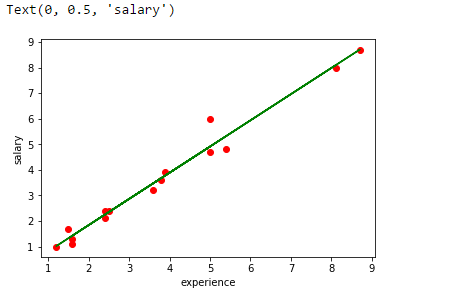
Analise o desempenho do modelo calculando o erro quadrado médio.

erro1 = salário - pred
se = np.sum(erro1 ** 2)
mse = se/n
print("erro quadrado significa é", mse)

Use a biblioteca scikit para confirmar as etapas anteriores.

from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error 
experience = experience.reshape(-1,1)
model = LinearRegression()
model.fit(experiência,salário)
salary_pred = modelo.prever(experiência)
Mse = mean_squared_error(salário, salary_pred)
imprimir('slop', model.coef_)
imprimir("Interceptar", model.intercept_)
imprimir("MSE", Mse)

Resumo

Em regressão, nós traçamos um gráfico entre as variáveis ​​que melhor se ajustam aos pontos de dados fornecidos. A regressão linear mostra a relação linear entre a variável independente (Eixo X) e a variável dependente (Eixo y).Para calcular a regressão linear da linha de melhor ajuste, uma forma tradicional de interceptação de declive é usada. Uma linha de regressão pode ser uma relação linear positiva ou uma relação linear negativa.

O objetivo do algoritmo de regressão linear é obter os melhores valores para a0 e a1 para encontrar a melhor linha de ajuste e a linha de ajuste melhor deve ter o menor erro.. Em regressão linear, Raiz do erro quadrático médio (MSE) a função de custo é usada, naquela ajuda a determinar os melhores valores possíveis para a0 e a1, que fornece a linha de melhor ajuste para os pontos de dados. Usando a função MSE, vamos alterar os valores de a0 e a1 para que o valor MSE seja definido para os mínimos. O gradiente descendente é um método de atualizar a0 e a1 para minimizar a função de custo (MSE)

A mídia mostrada neste artigo não é propriedade da DataPeaker e é usada a critério do autor.

Relacionado