Este artigo foi publicado como parte do Data Science Blogathon.
Introdução
APERTE PARA IMPACTO! CLAMP! CLAMP! CLAMP!
UPS!!! Nosso avião caiu, mas felizmente estamos todos seguros. Somos cientistas de dados, então queremos abrir a caixa preta e ver quais coisas aleatórias foram registradas dentro. sim, vamos passar ao nosso tópico.
O que são florestas aleatórias?
Você deve ter resolvido pelo menos uma vez um problema de probabilidade em sua escola, no qual deveria encontrar a probabilidade de obter uma bola de uma cor específica de uma bolsa contendo bolas de cores diferentes., dado o número de bolas de cada cor. As florestas aleatórias são simples se tentarmos aprendê-las com esta analogia em mente.
As florestas aleatórias (RF) eles são basicamente um saco contendo n árvores de decisão (DT) que têm um conjunto diferente de hiperparâmetros e são treinados em diferentes subconjuntos de dados. Digamos que tenho 100 árvores de decisão na minha bolsa florestal aleatória! Como eu acabei de dizer, estos árboles de decisión tienen un conjunto diferente de hiperparámetros y un subconjunto diferente de datos de TreinamentoO treinamento é um processo sistemático projetado para melhorar as habilidades, Conhecimento ou habilidades físicas. É aplicado em várias áreas, como esporte, Educação e desenvolvimento profissional. Um programa de treinamento eficaz inclui planejamento de metas, prática regular e avaliação do progresso. A adaptação às necessidades individuais e a motivação são fatores-chave para alcançar resultados bem-sucedidos e sustentáveis em qualquer disciplina...., então a decisão ou previsão dada por essas árvores pode variar muito. Vamos considerar que, de alguma forma, treinei todos esses 100 árvores com seus respectivos subconjuntos de dados. Agora vou perguntar às cem árvores na minha bolsa qual é a previsão deles nos meus dados de teste. Agora só precisamos tomar uma decisão sobre um exemplo ou dados de teste, nós fazemos isso por meio de um simples voto. Seguimos o que a maioria das árvores previu para aquele exemplo.
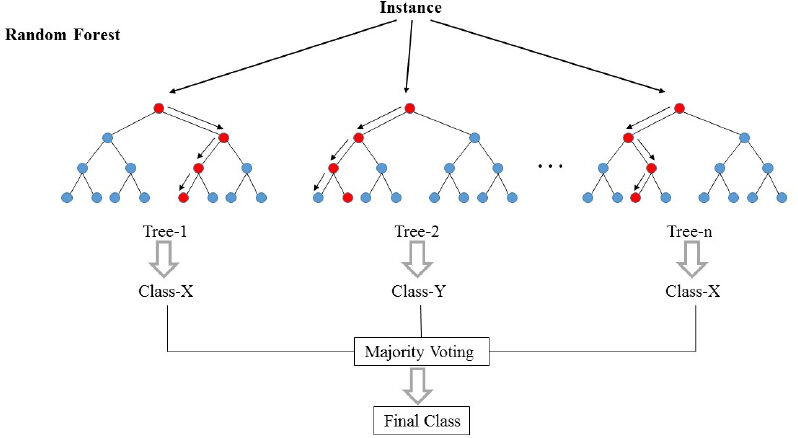
Na foto acima, podemos ver como um exemplo é classificado usando n árvores onde a previsão final é feita por meio de uma votação de todas as n árvores.
Na linguagem do aprendizado de máquina, RFs também são chamados de métodos de montagem ou ensacamento. Acho que a palavra bolsa pode vir da analogia que acabamos de discutir!!
Vamos nos aproximar um pouco mais de ML Jargons !!
El bosque aleatorio es básicamente un algoritmo de aprendizagem supervisionadaO aprendizado supervisionado é uma abordagem de aprendizado de máquina em que um modelo é treinado usando um conjunto de dados rotulados. Cada entrada no conjunto de dados está associada a uma saída conhecida, permitindo que o modelo aprenda a prever resultados para novas entradas. Este método é amplamente utilizado em aplicações como classificação de imagens, Reconhecimento de fala e previsão de tendências, destacando sua importância em.... Isso pode ser usado para tarefas de regressão e classificação. Mas discutiremos seu uso para classificação porque é mais intuitivo e fácil de entender.. A floresta aleatória é um dos algoritmos mais utilizados pela sua simplicidade e estabilidade.
Ao construir subconjuntos de dados para árvores, palavra “aleatória” entra em cena. Um subconjunto de dados é criado selecionando aleatoriamente x número de recursos (colunas) y y número de exemplos (filas) do conjunto de dados original de n características e m exemplos.
Florestas aleatórias são mais estáveis e confiáveis do que apenas uma árvore de decisão. Isso significa simplesmente que é melhor votar em todos os ministros do que simplesmente aceitar a decisão dada pelo primeiro-ministro..
Como vimos, as florestas aleatórias nada mais são do que a coleção de árvores de decisão, torna-se essencial conhecer a árvore de decisão. Então, vamos mergulhar nas árvores de decisão.
O que é uma árvore de decisão?
Em palavras muito simples, é um “Conjunto de regras” criado ao aprender com um conjunto de dados que pode ser usado para fazer previsões sobre dados futuros. Tentaremos entender isso com um exemplo.
Aqui está um pequeno conjunto de dados simples. Neste conjunto de dados, as primeiras quatro características são características independentes e as quatro últimas são características dependentes. As características independentes descrevem as condições climáticas em um determinado dia e a característica dependente nos diz se fomos ou não capazes de jogar tênis naquele dia..
Agora vamos tentar criar algumas regras usando características independentes para prever características dependentes. Apenas por observação, podemos ver que se o Outlook estiver nublado, o jogo é sempre sim, independentemente de outras características. de forma similar, podemos criar todas as regras para descrever completamente o conjunto de dados. Aqui estão todas as regras.
- R1: E (Outlook = Sunny) E (Umidade = Alta) Então jogar = não
- R2: E (Outlook = Sunny) E (Umidade = Normal) Então jogue = Sim
- R3: E (Outlook = Nublado) Então jogue = Sim
- R4: E (Outlook = Chuva) E (Vento = forte) Então jogar = não
- R5: E (Perspectiva = Chuva) E (Vento = Fraco) Então pague = Sim
Podemos facilmente converter essas regras em um diagrama de árvore. Aqui está o gráfico de árvore.
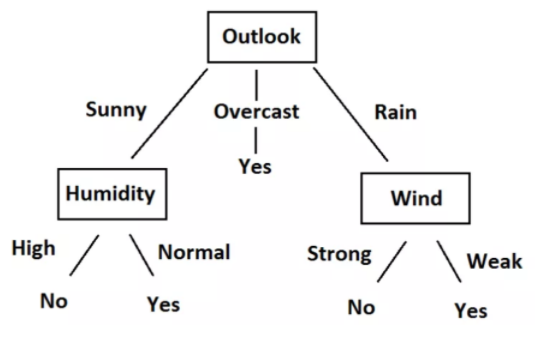
Olhando para os dados, as regras e a árvore, Você entenderá que agora podemos prever se devemos ou não jogar tênis., dada a situação climática com base em características independentes. Todo esse processo de criação de regras para um dado dado nada mais é do que o treinamento do modelo de árvore de decisão.
Poderíamos definir regras e fazer uma árvore apenas olhando aqui porque o conjunto de dados é tão pequeno. Mas, Como treinamos a árvore de decisão em um conjunto de dados maior? Para isso, precisamos saber um pouco de matemática. Agora vamos tentar entender a matemática por trás da árvore de decisão.
Conceitos matemáticos por trás da árvore de decisão
Esta seção consiste em dois conceitos importantes: Entropia e ganho de informação.
Entropia
La entropía es una mediro "medir" É um conceito fundamental em várias disciplinas, que se refere ao processo de quantificação de características ou magnitudes de objetos, Fenômenos ou situações. Na matemática, Usado para determinar comprimentos, Áreas e volumes, enquanto nas ciências sociais pode se referir à avaliação de variáveis qualitativas e quantitativas. A precisão da medição é crucial para obter resultados confiáveis e válidos em qualquer pesquisa ou aplicação prática.... de la aleatoriedad de un sistema. A entropia do espaço amostral S é o número esperado de bits necessários para codificar a classe de um membro sorteado aleatoriamente de S. Aqui temos 14 linhas em nossos dados, pelo que 14 membros.
Entropia E (S) = -∑p (x) * registro2(p (x))
A entropia do sistema é calculada usando a fórmula acima, onde p (x) é a probabilidade de obter a classe x daqueles 14 membros. Temos duas aulas aqui, um é Sim e o outro é Não na coluna Play. Tenho 9 Sim e 5 Não está em nosso conjunto de dados. Então, o cálculo da entropia aqui será o seguinte
E (S) = -[p(sim)*registro(p(sim))+ p(Não)*registro(p(Não))]= -[(9/14)*registro((9/14))+ (5/14*registro((5/14)))]= 0,94
Ganho de informação
O ganho de informação é a quantidade em que a Entropia do sistema é reduzida devido à divisão que fizemos. Nós criamos a árvore usando observações. Mas, Por que decidimos que devemos dividir os dados primeiro com base no Outlook e não em qualquer outra função? A razão é que essa divisão estava reduzindo a entropia pela quantidade máxima, mas fizemos isso intuitivamente no exemplo acima.
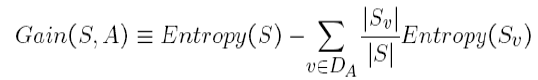
A divisão da árvore acima nos mostra que 9 Sim e 5 Eles não foram divididos como (2 E, 3 N), (4 E, 0 N), (3 E, 2 N), quando fazemos a divisão de acordo com a perspectiva. Os valores E abaixo de cada divisão mostram valores de entropia considerando-se um sistema completo e usando a fórmula de entropia acima. Mais tarde, calculamos o ganho de informação para a divisão do cliente potencial usando a fórmula de ganho acima.
de forma similar, podemos calcular o ganho de informação para cada divisão de recursos independentemente. E obtemos os seguintes resultados:
- Ganho (S, Panorama) = 0,247
- Ganho (S, umidade) = 0,151
- Ganho (S, vento) = 0.048
- Ganho (S, temperatura) = 0.029
Podemos ver que estamos obtendo o máximo ganho de informação ao dividir a função Outlook. Repetimos este procedimento para criar a árvore inteira. Eu espero que você tenha gostado de ler o artigo. Se você gostou do artigo, compartilhe com seus colegas e amigos. Leitura feliz!!!
