K significa agrupamento simplificado em Python

Visão geral

• O que é K significa Clustering?
• Implementação de K significa Clustering
• WCSS e método cotovelo para encontrar o número de clusters
• Implementação Python do K Means Clustering

K significa é um dos algoritmos de aprendizado de máquina não supervisionados mais populares usados ​​para resolver problemas de classificação. K significa que ele segrega os dados não rotulados em vários grupos, chamados clusters, baseado em ter características semelhantes, padrões comuns.

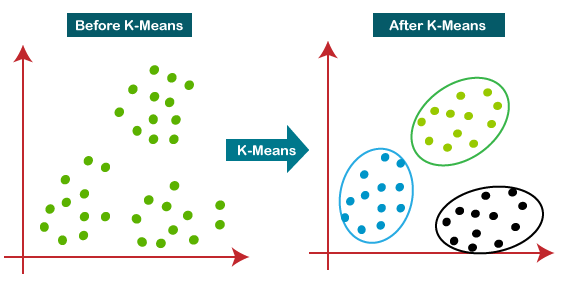
Tabela de conteúdo

1. O que é aglomeração?
2. O que significa o algoritmo de K?
3. Implementação esquemática do cluster KMeans
4. Escolha o número correto de clusters
5. Implementação Python

1. O que é aglomeração?

Suponha que temos um número N de conjuntos de dados multivariados não rotulados de vários animais, como cães, gatos, pássaros, etc. A técnica para segregar conjuntos de dados em vários grupos, baseado em ter características e características semelhantes, isso se chama agrupamento..

Os grupos que são formados são conhecidos como Clusters. A técnica de clustering está sendo usada em vários campos, como reconhecimento de imagem, filtragem de spam

La agrupación en clústeres se utiliza en el algoritmo de Aprendizado não supervisionadoO aprendizado não supervisionado é uma técnica de aprendizado de máquina que permite que os modelos identifiquem padrões e estruturas em dados sem rótulos predefinidos. Por meio de algoritmos como k-means e análise de componentes principais, Essa abordagem é usada em uma variedade de aplicações, como segmentação de clientes, detecção de anomalias e compactação de dados. Sua capacidade de revelar informações ocultas o torna uma ferramenta valiosa no... en el aprendizaje automático como dados multivariados podem ser segregados em vários grupos, sem nenhum supervisor, com base em um padrão comum oculto em conjuntos de dados.

2. O que significa o algoritmo de K?

O algoritmo Kmeans é um algoritmo iterativo que divide um grupo de n conjuntos de dados em k subgrupos / clusters com base na semelhança e sua distância média do centroide desse subgrupo / formado em particular..

K, aqui está o número predefinido de clusters que o algoritmo irá formar. Se K = 3, significa que o número de clusters que serão formados a partir do conjunto de dados é 3

Etapas do algoritmo K significa

A operação do algoritmo K-Means é explicada nas etapas a seguir:

Paso 1: Selecione o valor de K para decidir o número de clusters a serem formados.

Paso 2: Selecione K pontos aleatórios que atuarão como centróides.

Paso 3: Mapeie cada ponto de dados, com base em sua distância de pontos selecionados aleatoriamente (centroide), para o centróide mais próximo / close que formará os grupos predefinidos.

Paso 4: coloque um novo centroide de cada grupo.

Paso 5: Repita o passo 3, que reatribui cada ponto de dados ao novo centroide mais próximo de cada grupo.

Paso 6: Se ocorrer alguma reatribuição, vá para o passo 4; pelo contrário, vá para o passo 7.

Paso 7: TERMINAR

3. A implementação esquemática de K significa agrupamento

PASO 1:Vamos escolher o número k de clusters, quer dizer, K = 2, para segregar o conjunto de dados e colocá-los em diferentes clusters respectivos. vamos escolher alguns 2 pontos aleatórios que atuarão como centróides para formar o grupo.

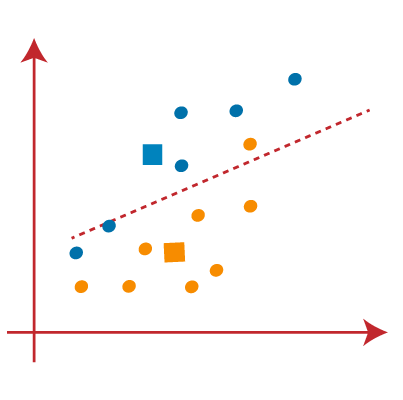
PASO 2: Ahora asignaremos cada punto de datos a un Diagrama de dispersãoO gráfico de dispersão é uma ferramenta gráfica usada em estatística para visualizar a relação entre duas variáveis. Consiste em um conjunto de pontos em um plano cartesiano, onde cada ponto representa um par de valores correspondentes às variáveis analisadas. Este tipo de gráfico permite identificar padrões, Tendências e possíveis correlações, facilitando a interpretação dos dados e a tomada de decisão com base nas informações visuais apresentadas.... basado en su distancia desde el punto K o centroide más cercano. Se hará dibujando una medianaA mediana é uma medida estatística que representa o valor central de um conjunto de dados ordenados. Para calculá-lo, Os dados são organizados do menor para o maior e o número no meio é identificado. Se houver um número par de observações, Os dois valores principais são calculados em média. Este indicador é especialmente útil em distribuições assimétricas, uma vez que não é afetado por valores extremos.... entre ambos centroides. Considere a seguinte imagem:

PASO 3: os pontos do lado esquerdo da linha estão perto do centroide azul e os pontos do lado direito da linha estão perto do centroide amarelo. O da esquerda forma um grupo com um centróide azul e o da direita com um centróide amarelo..

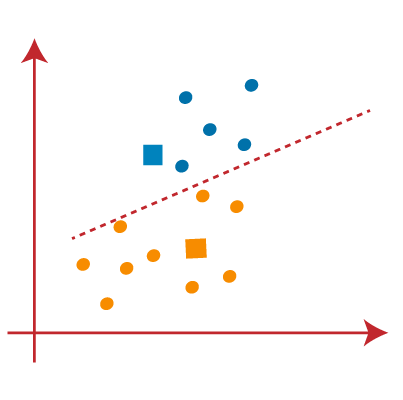
PASO 4:repita o processo escolhendo um novo centroide. Para escolher os novos centroides, encontraremos o novo centro de gravidade desses centróides, mostrado abaixo:

PASO 5: A seguir, vamos reatribuir cada ponto de dados ao novo centroide. Vamos repetir o mesmo processo anterior (usando uma linha mediana). O ponto de dados amarelo no lado azul da linha mediana será incluído no grupo azul

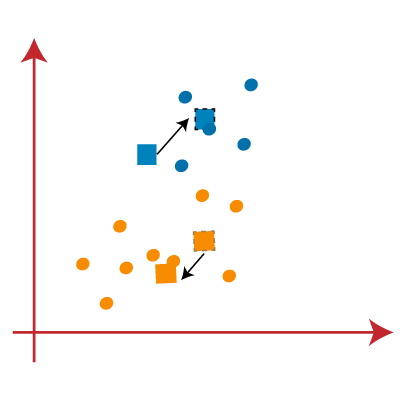
PASO 6: UMA mediro "medir" É um conceito fundamental em várias disciplinas, que se refere ao processo de quantificação de características ou magnitudes de objetos, Fenômenos ou situações. Na matemática, Usado para determinar comprimentos, Áreas e volumes, enquanto nas ciências sociais pode se referir à avaliação de variáveis qualitativas e quantitativas. A precisão da medição é crucial para obter resultados confiáveis e válidos em qualquer pesquisa ou aplicação prática.... que se haya realizado la reasignación, vamos repetir o passo anterior de encontrar novos centróides.

PASO 7: Vamos repetir o processo anterior de encontrar o centro de gravidade dos centróides, como é mostrado a seguir.

PASO 8: Depois de encontrar os novos centróides, vamos desenhar a linha mediana novamente e reatribuir os pontos de dados, como nos passos anteriores.

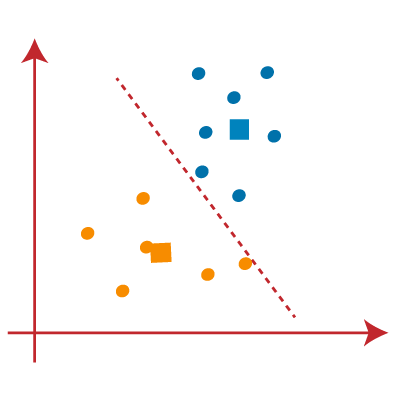
PASO 9: Finalmente, vamos segregar pontos com base na linha mediana, para que dois grupos sejam formados e nenhum ponto diferente seja incluído em um único grupo.

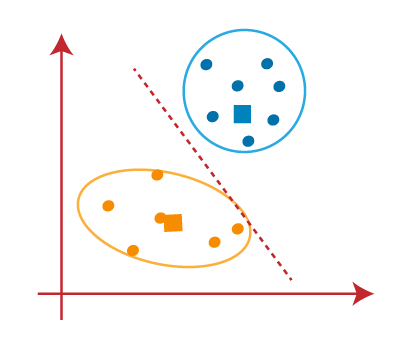
O grupo final que está sendo formado é o seguinte

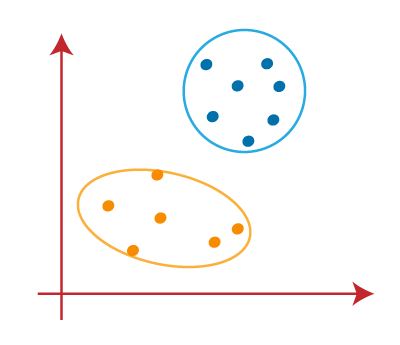
4. Escolha o número correto de clusters

O número de clusters que escolhemos para o algoritmo não deve ser aleatório. Cada cluster é formado calculando e comparando as distâncias médias de cada ponto de dados dentro de um cluster de seu centroide.

Podemos elegir el número correcto de clústeres con la ayuda del método de suma de cuadrados dentro del cachoUm cluster é um conjunto de empresas e organizações interconectadas que operam no mesmo setor ou área geográfica, e que colaboram para melhorar sua competitividade. Esses agrupamentos permitem o compartilhamento de recursos, Conhecimentos e tecnologias, Promover a inovação e o crescimento económico. Os clusters podem abranger uma variedade de setores, Da tecnologia à agricultura, e são fundamentais para o desenvolvimento regional e a criação de empregos.... (WCSS).

WCSS Representa a soma dos quadrados das distâncias dos pontos de dados em cada grupo de seu centroide.

A ideia principal é minimizar a distância entre os pontos de dados e o centroide dos clusters. O processo é iterado até atingir um valor mínimo para a soma das distâncias.

Para encontrar o valor ideal de clusters, método de cotovelo siga os passos abaixo:

1 Executar o agrupamentoo "agrupamento" É um conceito que se refere à organização de elementos ou indivíduos em grupos com características ou objetivos comuns. Este processo é usado em várias disciplinas, incluindo psicologia, Educação e biologia, para facilitar a análise e compreensão de comportamentos ou fenômenos. No campo educacional, por exemplo, O agrupamento pode melhorar a interação e o aprendizado entre os alunos, incentivando o trabalho.. de K-medias en un conjunto de datos dado para diferentes valores de K (variando de 1 al 10).

2 Para cada valor de K, calcula o valor WCSS.

3 Plotar um gráfico / curva entre os valores WCSS e o respectivo número de clusters K.

4 O ponto afiado da curvatura ou um ponto (que se parece com uma articulação cotovelo) da trama como um braço, será considerado como o melhor / valor ideal de K

5. Implementação Python

Importar bibliotecas relevantes

import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
de sklearn.cluster import KMeans

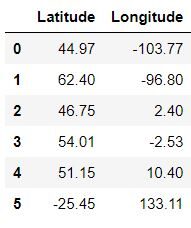
Carregando os dados

data = pd.read_csv('Countryclusters.csv')
dados

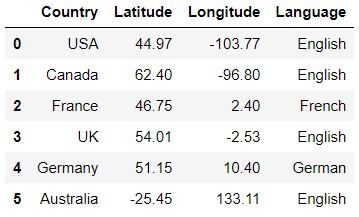
Gráfico dos dados

plt.scatter(dados['Comprimento'],dados['Latitude'])
plt.xlim(-180,180)
plt.ylim(-90,90)
plt.show()

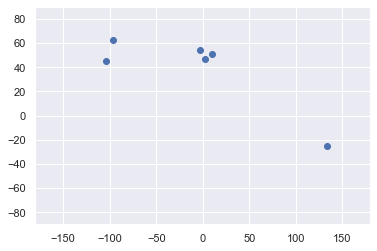
Selecione o recurso

 x = data.iloc[:,1:3] # 1t for rows and second for columns
x

Agrupamento

kmeans = KMeans(3)
significa.fit(x)

Resultados de agrupamento

identified_clusters = kmeans.fit_predict(x)
identified_clusters

variedade([1, 1, 0, 0, 0, 2])

data_with_clusters = data.copy()
data_with_clusters['Clusters'] = identified_clusters 
plt.scatter(data_with_clusters['Comprimento'],data_with_clusters['Latitude'],c=data_with_clusters['Clusters'],cmap='arco-íris')

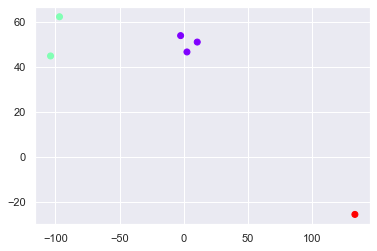
Tente um método diferente (para encontrar não. De grupos para selecionar)

Método WCSS e cotovelo

wcss=[]
para eu no alcance(1,7):
kmeans = KMeans(eu)
kmeans.fit(x)
wcss_iter = kmeans.inertia_
wcss.append(wcss_iter)

number_clusters = alcance(1,7)
plt.plot(number_clusters,wcss)
plt.title('O título do Cotovelo')
plt.xlabel('Número de clusters')
plt.ylabel('WCSS')

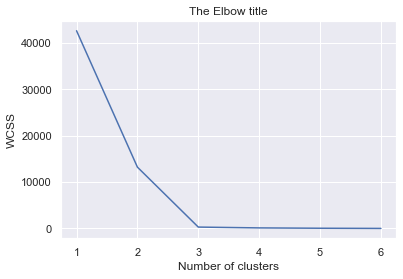
podemos escolher 3 É claro. de conglomerados, este método mostra o que o bom número de clusters são.

Com isso eu termino este blog.
Olá a todos, Namaste
Meu nome é Pranshu Sharma e sou um entusiasta da ciência de dados
Muito obrigado por dedicar seu valioso tempo para ler este blog.. Sinta-se à vontade para apontar quaisquer erros (depois de tudo, eu sou um aprendiz) e fornecer os comentários correspondentes ou deixar um comentário.
Dhanyvaad !!
Comentários:
Correio eletrônico: [e-mail protegido]

Relacionado