Implementar el aprendizaje automático con Caret en R

Introducción

Uno de los mayores desafíos que enfrentan los principiantes en el aprendizaje automático es en qué algoritmos aprender y en qué enfocarse. En el caso de R, el problema se ve acentuado por el hecho de que varios algoritmos tendrían una sintaxis diferente, diferentes parámetrosLos "parámetros" son variables o criterios que se utilizan para definir, medir o evaluar un fenómeno o sistema. En diversos campos como la estadística, la informática y la investigación científica, los parámetros son fundamentales para establecer normas y estándares que guían el análisis y la interpretación de datos. Su adecuada selección y manejo son cruciales para obtener resultados precisos y relevantes en cualquier estudio o proyecto.... para ajustar y diferentes requisitos en el formato de datos. Esto podría ser demasiado para un principiante.

Entonces, ¿cómo se puede transformar de un principiante a un científico de datos construyendo cientos de modelos y apilándolos juntos? Ciertamente no hay ningún atajo, pero lo que te diré hoy te permitirá aplicar cientos de modelos de aprendizaje automático sin tener que:

• recuerde los diferentes nombres de paquetes para cada algoritmo.
• sintaxis de la aplicación de cada algoritmo.
• parámetros para ajustar para cada algoritmo.

Todo esto ha sido posible gracias a los años de esfuerzo que han ido detrás CARET (EntrenamientoEl entrenamiento es un proceso sistemático diseñado para mejorar habilidades, conocimientos o capacidades físicas. Se aplica en diversas áreas, como el deporte, la educación y el desarrollo profesional. Un programa de entrenamiento efectivo incluye la planificación de objetivos, la práctica regular y la evaluación del progreso. La adaptación a las necesidades individuales y la motivación son factores clave para lograr resultados exitosos y sostenibles en cualquier disciplina.... de clasificación y regresión) que es posiblemente el proyecto más grande en R. Este paquete por sí solo es todo lo que necesita saber para resolver casi cualquier problema de aprendizaje automático supervisado. Proporciona una interfaz uniforme para varios algoritmos de aprendizaje automático y estandariza otras tareas como la división de datos, el preprocesamiento, la selección de funciones, la estimación de importancia variableEn estadística y matemáticas, una "variable" es un símbolo que representa un valor que puede cambiar o variar. Existen diferentes tipos de variables, como las cualitativas, que describen características no numéricas, y las cuantitativas, que representan cantidades numéricas. Las variables son fundamentales en experimentos y estudios, ya que permiten analizar relaciones y patrones entre diferentes elementos, facilitando la comprensión de fenómenos complejos...., etc.

Para obtener una descripción detallada de las diversas funcionalidades proporcionadas por Caret, puede consultar este artículo.

Hoy trabajaremos en el Problema de predicción de préstamos III para mostrarte el poder del paquete Caret.

PD Si bien caret definitivamente simplifica el trabajo hasta cierto punto, no puede quitarle el trabajo duro y la práctica que necesita para convertirse en un maestro en aprendizaje automático.

Tabla de contenido

1. Empezando
2. Preprocesamiento con Caret
3. Dividir los datos con Caret
4. Selección de funciones con Caret
5. Modelos de entrenamiento con Caret
6. Ajuste de parámetros con Caret
7. Estimación de importancia variable con Caret
8. Hacer predicciones con Caret

1. Empezando

En pocas palabras, Caret es esencialmente un contenedor para más de 200 algoritmos de aprendizaje automático. Además, proporciona varias características que lo convierten en una solución integral para todas las necesidades de modelado para problemas de aprendizaje automático supervisados.

Caret intenta no cargar todos los paquetes de los que depende al principio. En cambio, los carga solo cuando se necesitan los paquetes. Pero asume que ya tiene todos los algoritmos instalados en su sistema.

Para instalar Caret en su sistema, use el siguiente comando. Aviso: puede llevar algún tiempo:

> install.packages("caret", dependencies = c("Depends", "Suggests"))

Ahora, comencemos a usar el paquete de intercalación en Problema de predicción de préstamos 3:

#Loading caret package library("caret") #Loading training data train<-read.csv("train_u6lujuX_CVtuZ9i.csv",stringsAsFactors = T) #Looking at the structure of caret package. str(train) #'data.frame':         614 obs. of  13 variables: #$ Loan_ID          : Factor w/ 614 levels "LP001002","LP001003",..: 1 2 3 4 5 6 7 8 9 #10 .. #$ Gender           : Factor w/ 3 levels "","Female","Male": 3 3 3 3 3 3 3 3 3 3 ... #$ Married          : Factor w/ 3 levels "","No","Yes": 2 3 3 3 2 3 3 3 3 3 ... #$ Dependents       : Factor w/ 5 levels "","0","1","2",..: 2 3 2 2 2 4 2 5 4 3 ... #$ Education        : Factor w/ 2 levels "Graduate","Not Graduate": 1 1 1 2 1 1 2 1 1 #1 ... #$ Self_Employed    : Factor w/ 3 levels "","No","Yes": 2 2 3 2 2 3 2 2 2 2 ... #$ ApplicantIncome  : int  5849 4583 3000 2583 6000 5417 2333 3036 4006 12841 #... #$ CoapplicantIncome: num  0 1508 0 2358 0 ... #$ LoanAmount       : int  NA 128 66 120 141 267 95 158 168 349 ... #$ Loan_Amount_Term : int  360 360 360 360 360 360 360 360 360 360 ... #$ Credit_History   : int  1 1 1 1 1 1 1 0 1 1 ... #$ Property_Area    : Factor w/ 3 levels "Rural","Semiurban",..: 3 1 3 3 3 3 3 2 3 2 #... #$ Loan_Status      : Factor w/ 2 levels "N","Y": 2 1 2 2 2 2 2 1 2 1 ...

En este problema, tenemos que predecir el estado del préstamo de una persona en función de su perfil.

2. Procesamiento previo con Caret

Necesitamos preprocesar nuestros datos antes de poder usarlos para modelar. Comprobemos si a los datos les faltan valores:

sum(is.na(train)) #[1] 86

A continuación, usemos Caret para imputar estos valores perdidos usando el algoritmo KNN. Predeciremos estos valores perdidos en función de otros atributos para esa fila. Además, escalaremos y centraremos los datos numéricos utilizando el conveniente preproceso () en Caret.

#Imputing missing values using KNN.Also centering and scaling numerical columns preProcValues <- preProcess(train, method = c("knnImpute","center","scale")) library('RANN') train_processed <- predict(preProcValues, train) sum(is.na(train_processed)) #[1] 0

También es muy fácil usar una codificación en caliente en Caret para crear variables ficticias para cada nivel de una variable categórica. Pero primero, convertiremos la variable dependiente en numérica.

#Converting outcome variable to numeric train_processed$Loan_Status<-ifelse(train_processed$Loan_Status=='N',0,1) id<-train_processed$Loan_ID train_processed$Loan_ID<-NULL #Checking the structure of processed train file str(train_processed) #'data.frame':         614 obs. of  12 variables: #$ Gender           : Factor w/ 3 levels "","Female","Male": 3 3 3 3 3 3 3 3 3 3 ... #$ Married          : Factor w/ 3 levels "","No","Yes": 2 3 3 3 2 3 3 3 3 3 ... #$ Dependents       : Factor w/ 5 levels "","0","1","2",..: 2 3 2 2 2 4 2 5 4 3 ... #$ Education        : Factor w/ 2 levels "Graduate","Not Graduate": 1 1 1 2 1 1 2 1 1 #1 ... #$ Self_Employed    : Factor w/ 3 levels "","No","Yes": 2 2 3 2 2 3 2 2 2 2 ... #$ ApplicantIncome  : num  0.0729 -0.1343 -0.3934 -0.4617 0.0976 ... #$ CoapplicantIncome: num  -0.554 -0.0387 -0.554 0.2518 -0.554 ... #$ LoanAmount       : num  0.0162 -0.2151 -0.9395 -0.3086 -0.0632 ... #$ Loan_Amount_Term : num  0.276 0.276 0.276 0.276 0.276 ... #$ Credit_History   : num  0.432 0.432 0.432 0.432 0.432 ... #$ Property_Area    : Factor w/ 3 levels "Rural","Semiurban",..: 3 1 3 3 3 3 3 2 3 2 #... #$ Loan_Status      : num  1 0 1 1 1 1 1 0 1 0 ...

Ahora, creando variables ficticias usando una codificación en caliente:

#Converting every categorical variable to numerical using dummy variables dmy <- dummyVars(" ~ .", data = train_processed,fullRank = T) train_transformed <- data.frame(predict(dmy, newdata = train_processed)) #Checking the structure of transformed train file str(train_transformed) #'data.frame':         614 obs. of  19 variables: #$ Gender.Female          : num  0 0 0 0 0 0 0 0 0 0 ... #$ Gender.Male            : num  1 1 1 1 1 1 1 1 1 1 ... #$ Married.No             : num  1 0 0 0 1 0 0 0 0 0 ... #$ Married.Yes            : num  0 1 1 1 0 1 1 1 1 1 ... #$ Dependents.0           : num  1 0 1 1 1 0 1 0 0 0 ... #$ Dependents.1           : num  0 1 0 0 0 0 0 0 0 1 ... #$ Dependents.2           : num  0 0 0 0 0 1 0 0 1 0 ... #$ Dependents.3.          : num  0 0 0 0 0 0 0 1 0 0 ... #$ Education.Not.Graduate : num  0 0 0 1 0 0 1 0 0 0 ... #$ Self_Employed.No       : num  1 1 0 1 1 0 1 1 1 1 ... #$ Self_Employed.Yes      : num  0 0 1 0 0 1 0 0 0 0 ... #$ ApplicantIncome        : num  0.0729 -0.1343 -0.3934 -0.4617 0.0976 ... #$ CoapplicantIncome      : num  -0.554 -0.0387 -0.554 0.2518 -0.554 ... #$ LoanAmount             : num  0.0162 -0.2151 -0.9395 -0.3086 -0.0632 ... #$ Loan_Amount_Term       : num  0.276 0.276 0.276 0.276 0.276 ... #$ Credit_History         : num  0.432 0.432 0.432 0.432 0.432 ... #$ Property_Area.Semiurban: num  0 0 0 0 0 0 0 1 0 1 ... #$ Property_Area.Urban    : num  1 0 1 1 1 1 1 0 1 0 ... #$ Loan_Status            : num  1 0 1 1 1 1 1 0 1 0 ... #Converting the dependent variable back to categorical train_transformed$Loan_Status<-as.factor(train_transformed$Loan_Status)

Aquí, «fullrank = T» creará solo (n-1) columnas para una columna categórica con n niveles diferentes. Esto funciona especialmente para los predictores categóricos que representan como género, casado, etc., donde solo tenemos dos niveles: Masculino / Femenino, Sí / No, etc. porque 0 se puede usar para representar una clase mientras que 1 representa la otra clase en la misma columna.

3. Dividir datos usando el símbolo de intercalación

Crearemos un conjunto de validación cruzada a partir del conjunto de entrenamiento para evaluar nuestro modelo. Es importante confiar más en el conjunto de validación cruzada para la evaluación real de su modelo, de lo contrario, podría terminar sobreajustando la tabla de clasificación pública.

Usaremos createDataPartition () para dividir nuestros datos de entrenamiento en dos conjuntos: 75% y 25%. Dado que nuestra variable de resultado es de naturaleza categórica, esta función se asegurará de que la distribución de las clases de variables de resultado sea similar en ambos conjuntos.

#Spliting training set into two parts based on outcome: 75% and 25% index <- createDataPartition(train_transformed$Loan_Status, p=0.75, list=FALSE) trainSet <- train_transformed[ index,] testSet <- train_transformed[-index,] #Checking the structure of trainSet str(trainSet) #'data.frame':         461 obs. of  19 variables: #$ Gender.Female          : num  0 0 0 0 0 0 0 0 0 0 ... #$ Gender.Male            : num  1 1 1 1 1 1 1 1 1 1 ... #$ Married.No             : num  1 0 0 0 1 0 0 0 0 0 ... #$ Married.Yes            : num  0 1 1 1 0 1 1 1 1 1 ... #$ Dependents.0           : num  1 0 1 1 1 0 1 0 0 0 ... #$ Dependents.1           : num  0 1 0 0 0 0 0 0 1 0 ... #$ Dependents.2           : num  0 0 0 0 0 1 0 0 0 1 ... #$ Dependents.3.          : num  0 0 0 0 0 0 0 1 0 0 ... #$ Education.Not.Graduate : num  0 0 0 1 0 0 1 0 0 0 ... #$ Self_Employed.No       : num  1 1 0 1 1 0 1 1 1 1 ... #$ Self_Employed.Yes      : num  0 0 1 0 0 1 0 0 0 0 ... #$ ApplicantIncome        : num  0.0729 -0.1343 -0.3934 -0.4617 0.0976 ... #$ CoapplicantIncome      : num  -0.554 -0.0387 -0.554 0.2518 -0.554 ... #$ LoanAmount             : num  0.0162 -0.2151 -0.9395 -0.3086 -0.0632 ... #$ Loan_Amount_Term       : num  0.276 0.276 0.276 0.276 0.276 ... #$ Credit_History         : num  0.432 0.432 0.432 0.432 0.432 ... #$ Property_Area.Semiurban: num  0 0 0 0 0 0 0 1 1 0 ... #$ Property_Area.Urban    : num  1 0 1 1 1 1 1 0 0 1 ... #$ Loan_Status            : Factor w/ 2 levels "0","1": 2 1 2 2 2 2 2 1 1 2 ...

4. Selección de funciones con Caret

La selección de características es una parte extremadamente crucial del modelado. Para comprender la importancia de la selección de funciones y las diversas técnicas utilizadas para la selección de funciones, le recomiendo encarecidamente que lea mi artículo anterior. Por ahora, usaremos la eliminación de características recursivas, que es un método contenedor para encontrar el mejor subconjunto de características para usar en el modelado.

#Feature selection using rfe in caret
control <- rfeControl(functions = rfFuncs,                    method = "repeatedcv",                    repeats = 3,                    verbose = FALSE) outcomeName<-'Loan_Status' predictors<-names(trainSet)[!names(trainSet) %in% outcomeName] Loan_Pred_Profile <- rfe(trainSet[,predictors], trainSet[,outcomeName],                       rfeControl = control) Loan_Pred_Profile #Recursive feature selection #Outer resampling method: Cross-Validated (10 fold, repeated 3 times) #Resampling performance over subset size: #  Variables Accuracy  Kappa AccuracySD KappaSD Selected #4   0.7737 0.4127    0.03707 0.09962         #8   0.7874 0.4317    0.03833 0.11168         #16   0.7903 0.4527    0.04159 0.11526         #18   0.7882 0.4431    0.03615 0.10812         #The top 5 variables (out of 16): #  Credit_History, LoanAmount, Loan_Amount_Term, ApplicantIncome, CoapplicantIncome #Taking only the top 5 predictors predictors<-c("Credit_History", "LoanAmount", "Loan_Amount_Term", "ApplicantIncome", "CoapplicantIncome")

5. Modelos de entrenamiento con Caret

Esta es probablemente la parte en la que Caret se destaca de cualquier otro paquete disponible. Proporciona la capacidad de implementar más de 200 algoritmos de aprendizaje automático utilizando una sintaxis coherente. Para obtener una lista de todos los algoritmos que admite Caret, puede usar:

names(getModelInfo())
#[1] "ada"                 "AdaBag"              "AdaBoost.M1"         "adaboost"           #[5] "amdai"               "ANFIS"               "avNNet"              "awnb"               #[9] "awtan"               "bag"                 "bagEarth"            "bagEarthGCV"        #[13] "bagFDA"              "bagFDAGCV"           "bam"                 "bartMachine"        #[17] "bayesglm"            "bdk"                 "binda"               "blackboost"         #[21] "blasso"              "blassoAveraged"      "Boruta"              "bridge"              #…. #[205] "svmBoundrangeString" "svmExpoString"       "svmLinear"           "svmLinear2"         #[209] "svmLinear3"          "svmLinearWeights"    "svmLinearWeights2"   "svmPoly"            #[213] "svmRadial"           "svmRadialCost"       "svmRadialSigma"      "svmRadialWeights"   #[217] "svmSpectrumString"   "tan"                 "tanSearch"           "treebag"            #[221] "vbmpRadial"          "vglmAdjCat"          "vglmContRatio"       "vglmCumulative"     #[225] "widekernelpls"       "WM"                  "wsrf"                "xgbLinear"          #[229] "xgbTree"             "xyf"

Para obtener más detalles de cualquier modelo, puede consultar aquí.

Simplemente podemos aplicar una gran cantidad de algoritmos con una sintaxis similar. Por ejemplo, para aplicar GBM, bosque aleatorio, red neuronalLas redes neuronales son modelos computacionales inspirados en el funcionamiento del cerebro humano. Utilizan estructuras conocidas como neuronas artificiales para procesar y aprender de los datos. Estas redes son fundamentales en el campo de la inteligencia artificial, permitiendo avances significativos en tareas como el reconocimiento de imágenes, el procesamiento del lenguaje natural y la predicción de series temporales, entre otros. Su capacidad para aprender patrones complejos las hace herramientas poderosas... y regresión logística:

model_gbm<-train(trainSet[,predictors],trainSet[,outcomeName],method='gbm') model_rf<-train(trainSet[,predictors],trainSet[,outcomeName],method='rf') model_nnet<-train(trainSet[,predictors],trainSet[,outcomeName],method='nnet') model_glm<-train(trainSet[,predictors],trainSet[,outcomeName],method='glm')

Puede continuar sintonizando los parámetros en todos estos algoritmos utilizando las técnicas de ajuste de parámetros.

6. Ajuste de parámetros con Caret

Es extremadamente fácil ajustar los parámetros usando Caret. Normalmente, el ajuste de parámetros en Caret se realiza de la siguiente manera:

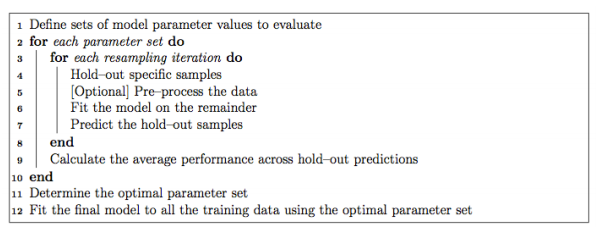
Es posible personalizar casi todos los pasos del proceso de ajuste. La técnica de remuestreo utilizada para evaluar el rendimiento del modelo utilizando un conjunto de parámetros en Caret de forma predeterminada es bootstrap, pero proporciona alternativas para usar k-fold, k-fold repetido y la validación cruzada Leave-one-out (LOOCV) que se puede especificar usando trainControl (). En este ejemplo, usaremos la validación cruzada de 5 partes repetida 5 veces.

fitControl <- trainControl(   method = "repeatedcv",   number = 5,   repeats = 5)

Si el espacio de búsqueda de parámetros no está definido, Caret usará 3 valores aleatorios de cada parámetro ajustable y usará los resultados de la validación cruzada para encontrar el mejor conjunto de parámetros para ese algoritmo. De lo contrario, hay dos formas más de ajustar los parámetros:

6.1.Uso de tuneGrid

Para encontrar los parámetros de un modelo que se pueden ajustar, puede utilizar

modelLookup(model="gbm") #model         parameter                   label forReg forClass probModel #1   gbm           n.trees   # Boosting Iterations   TRUE     TRUE      TRUE #2   gbm interaction.depth          Max Tree Depth   TRUE     TRUE      TRUE #3   gbm         shrinkage               Shrinkage   TRUE     TRUE      TRUE #4   gbm    n.minobsinnode Min. Terminal Node Size   TRUE     TRUE      TRUE #using grid search #Creating grid grid <- expand.grid(n.trees=c(10,20,50,100,500,1000),shrinkage=c(0.01,0.05,0.1,0.5),n.minobsinnode = c(3,5,10),interaction.depth=c(1,5,10)) # training the model model_gbm<-train(trainSet[,predictors],trainSet[,outcomeName],method='gbm',trControl=fitControl,tuneGrid=grid) # summarizing the model print(model_gbm) #Stochastic Gradient Boosting #461 samples #5 predictor #2 classes: '0', '1' #No pre-processing #Resampling: Cross-Validated (5 fold, repeated 5 times) #Summary of sample sizes: 368, 370, 369, 369, 368, 369, ... #Resampling results across tuning parameters: #  shrinkage  interaction.depth  n.minobsinnode  n.trees  Accuracy   Kappa    #0.01        1                  3                10     0.6876416  0.0000000 #0.01        1                  3                20     0.6876416  0.0000000 #0.01        1                  3                50     0.7982345  0.4423609 #0.01        1                  3               100     0.7952190  0.4364383 #0.01        1                  3               500     0.7904882  0.4342300 #0.01        1                  3              1000     0.7913627  0.4421230 #0.01        1                  5                10     0.6876416  0.0000000 #0.01        1                  5                20     0.6876416  0.0000000 #0.01        1                  5                50     0.7982345  0.4423609 #0.01        1                  5               100     0.7943635  0.4351912 #0.01        1                  5               500     0.7930783  0.4411348 #0.01        1                  5              1000     0.7913720  0.4417463 #0.01        1                 10                10     0.6876416  0.0000000 #0.01        1                 10                20     0.6876416  0.0000000 #0.01        1                 10                50     0.7982345  0.4423609 #0.01        1                 10               100     0.7943635  0.4351912 #0.01        1                 10               500     0.7939525  0.4426503 #0.01        1                 10              1000     0.7948362  0.4476742 #0.01        5                  3                10     0.6876416  0.0000000 #0.01        5                  3                20     0.6876416  0.0000000 #0.01        5                  3                50     0.7960556  0.4349571 #0.01        5                  3               100     0.7934987  0.4345481 #0.01        5                  3               500     0.7775055  0.4147204 #... #0.50        5                 10               100     0.7045617  0.2834696 #0.50        5                 10               500     0.6924480  0.2650477 #0.50        5                 10              1000     0.7115234  0.3050953 #0.50       10                  3                10     0.7389117  0.3681917 #0.50       10                  3                20     0.7228519  0.3317001 #0.50       10                  3                50     0.7180833  0.3159445 #0.50       10                  3               100     0.7172417  0.3189655 #0.50       10                  3               500     0.7058472  0.3098146 #0.50       10                  3              1000     0.7001852  0.2967784 #0.50       10                  5                10     0.7266895  0.3378430 #0.50       10                  5                20     0.7154746  0.3197905 #0.50       10                  5                50     0.7063535  0.2984819 #0.50       10                  5               100     0.7151012  0.3141440 #0.50       10                  5               500     0.7108516  0.3146822 #0.50       10                  5              1000     0.7147320  0.3225373 #0.50       10                 10                10     0.7314871  0.3327504 #0.50       10                 10                20     0.7150814  0.3081869 #0.50       10                 10                50     0.6993723  0.2815981 #0.50       10                 10               100     0.6977416  0.2719140 #0.50       10                 10               500     0.7037864  0.2854748 #0.50       10                 10              1000     0.6995610  0.2869718

Se utilizó la precisión para seleccionar el modelo óptimo utilizando el valor más grande.

Los valores finales utilizados para el modelo fueron n. Árboles = 10, profundidad de interacción = 1, contracción = 0.05 y n. Aminobsinnodo = 3

plot(model_gbm)

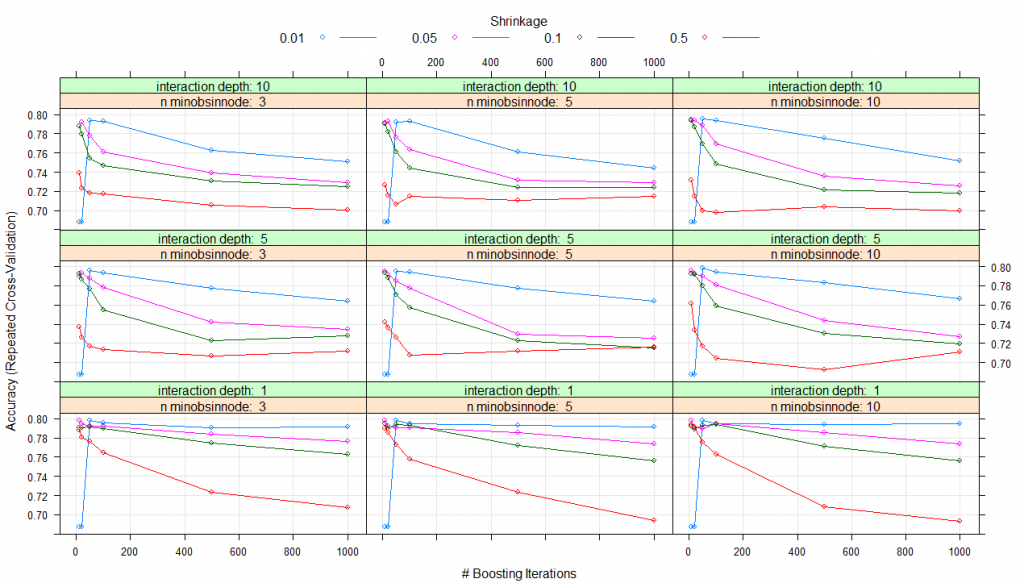
Por lo tanto, para todas las combinaciones de parámetros que enumeró en expand.grid (), se creará y probará un modelo mediante validación cruzada. El conjunto de parámetros con el mejor rendimiento de validación cruzada se utilizará para crear el modelo final que obtendrá al final.

6.2. Usando tuneLength

En lugar de especificar los valores exactos para cada parámetro de ajuste, simplemente podemos pedirle que use cualquier número de valores posibles para cada parámetro de ajuste a través de tuneLength. Probemos un ejemplo usando tuneLength = 10.

#using tune length model_gbm<-train(trainSet[,predictors],trainSet[,outcomeName],method='gbm',trControl=fitControl,tuneLength=10) print(model_gbm) #Stochastic Gradient Boosting #461 samples #5 predictor #2 classes: '0', '1' #No pre-processing #Resampling: Cross-Validated (5 fold, repeated 5 times) #Summary of sample sizes: 368, 369, 369, 370, 368, 369, ... #Resampling results across tuning parameters: #  interaction.depth  n.trees  Accuracy   Kappa    #1                  50      0.7978084  0.4541008 #1                 100      0.7978177  0.4566764 #1                 150      0.7934792  0.4472347 #1                 200      0.7904310  0.4424091 #1                 250      0.7869714  0.4342797 #1                 300      0.7830488  0.4262414 ... #10                 100      0.7575230  0.3860319 #10                 150      0.7479757  0.3719707 #10                 200      0.7397290  0.3566972 #10                 250      0.7397285  0.3561990 #10                 300      0.7362552  0.3513413 #10                 350      0.7340812  0.3453415 #10                 400      0.7336416  0.3453117 #10                 450      0.7306027  0.3415153 #10                 500      0.7253854  0.3295929

El parámetro de ajuste ‘contracción’ se mantuvo constante en un valor de 0,1

El parámetro de ajuste ‘n.minobsinnode’ se mantuvo constante en un valor de 10

Se utilizó la precisión para seleccionar el modelo óptimo utilizando el valor más grande.

Los valores finales utilizados para el modelo fueron n. Árboles = 50, profundidad de interacción = 2, contracción = 0,1 y n. Aminobsinnodo = 10.

plot(model_gbm)

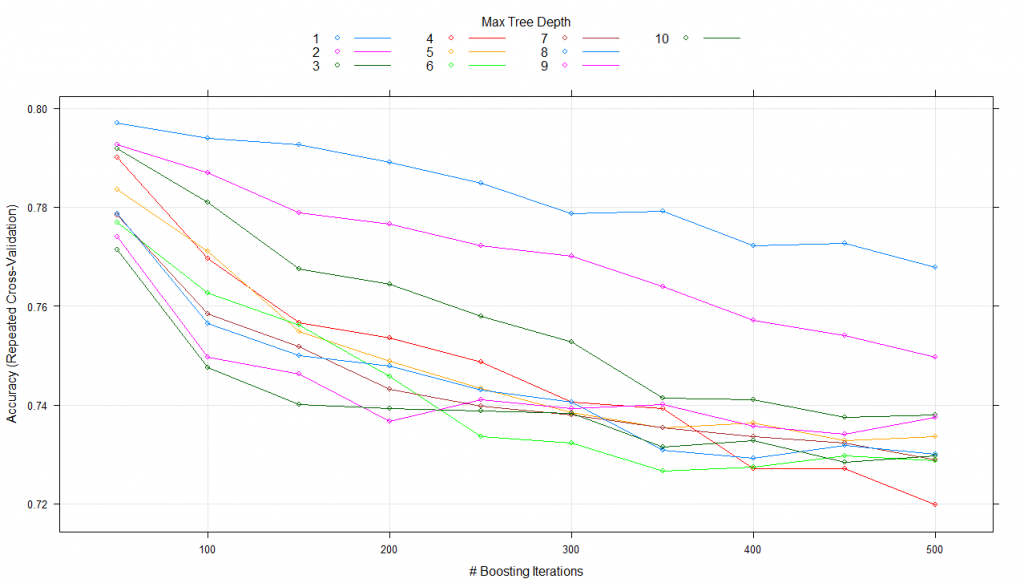
Aquí, mantiene constantes los parámetros de contracción y n. Aminobsinnodo mientras que altera n. Árboles y la profundidad de interacción sobre 10 valores y utiliza la mejor combinación para entrenar el modelo final.

7. Estimación de la importancia de la variable mediante intercalación

Caret también hace que las estimaciones de importancia de las variables sean accesibles con el uso de varImp () para cualquier modelo. Echemos un vistazo a la importancia de la variable para los cuatro modelos que creamos:

#Checking variable importance for GBM #Variable Importance varImp(object=model_gbm) #gbm variable importance #Overall #Credit_History    100.000 #LoanAmount         16.633 #ApplicantIncome     7.104 #CoapplicantIncome   6.773 #Loan_Amount_Term    0.000 #Plotting Varianle importance for GBM plot(varImp(object=model_gbm),main="GBM - Variable Importance")

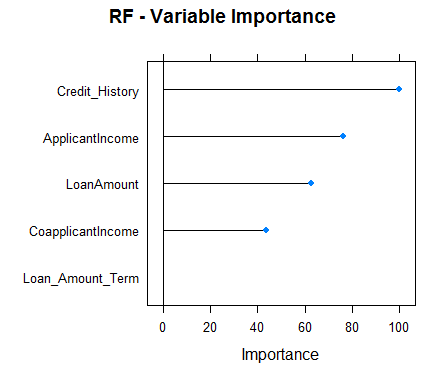
#Checking variable importance for RF varImp(object=model_rf) #rf variable importance #Overall #Credit_History     100.00 #ApplicantIncome     73.46 #LoanAmount          60.59 #CoapplicantIncome   40.43 #Loan_Amount_Term     0.00 #Plotting Varianle importance for Random Forest plot(varImp(object=model_rf),main="RF - Variable Importance")

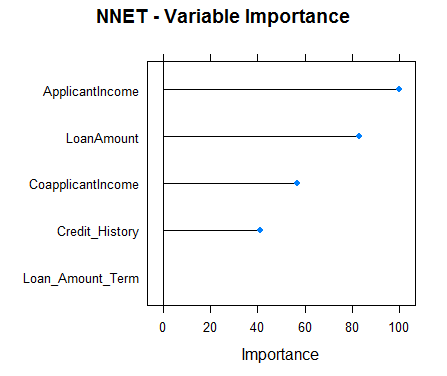
#Checking variable importance for NNET varImp(object=model_nnet) #nnet variable importance #Overall #ApplicantIncome    100.00 #LoanAmount          82.87 #CoapplicantIncome   56.92 #Credit_History      41.11 #Loan_Amount_Term     0.00 #Plotting Variable importance for Neural Network plot(varImp(object=model_nnet),main="NNET - Variable Importance")

#Checking variable importance for GLM varImp(object=model_glm) #glm variable importance #Overall #Credit_History    100.000 #CoapplicantIncome  17.218 #Loan_Amount_Term   12.988 #LoanAmount          5.632 #ApplicantIncome     0.000 #Plotting Variable importance for GLM plot(varImp(object=model_glm),main="GLM - Variable Importance")

Claramente, las estimaciones de importancia variable de diferentes modelos difieren y, por lo tanto, podrían usarse para obtener una visión más holística de la importancia de cada predictor. Dos usos principales de importancia variable de varios modelos son:

• Los predictores que son importantes para la mayoría de los modelos representan predictores realmente importantes.
• En conjunto, deberíamos usar predicciones de modelos que tienen una importancia variable significativamente diferente, ya que también se espera que sus predicciones sean diferentes. Aunque, una cosa que debe asegurarse es que todos ellos sean lo suficientemente precisos.

8. Predicciones con Caret

Para predecir la variable dependiente para el conjunto de pruebas, Caret ofrece predict.train (). Debe especificar el nombre del modelo, los datos de prueba. Para problemas de clasificación, Caret también ofrece otra característica denominada type que se puede configurar como «prob» o «raw». Para type = ”raw”, las predicciones serán solo las clases de resultado para los datos de prueba, mientras que para type = ”prob”, dará probabilidades de ocurrencia de cada observación en varias clases de la variable de resultado.

Echemos un vistazo a las predicciones de nuestro modelo GBM:

#Predictions predictions<-predict.train(object=model_gbm,testSet[,predictors],type="raw") table(predictions) #predictions #0   1 #28 125

Caret también proporciona una función confusionMatrix que proporcionará la matriz de confusión junto con varias otras métricas para sus predicciones. Aquí está el análisis de rendimiento de nuestro modelo GBM:

confusionMatrix(predictions,testSet[,outcomeName]) #Confusion Matrix and Statistics #Reference #Prediction   0   1 #0  25   3 #1  23 102 #Accuracy : 0.8301         #95% CI : (0.761, 0.8859) #No Information Rate : 0.6863         #P-Value [Acc > NIR] : 4.049e-05      #Kappa : 0.555          #Mcnemar's Test P-Value : 0.0001944      #Sensitivity : 0.5208         #Specificity : 0.9714         #Pos Pred Value : 0.8929 #Neg Pred Value : 0.8160         #Prevalence : 0.3137         #Detection Rate : 0.1634         #Detection Prevalence : 0.1830         #Balanced Accuracy : 0.7461         #'Positive' Class : 0

Recursos adicionales

Notas finales

Caret es uno de los paquetes más poderosos y útiles jamás creados en R. Solo tiene la capacidad de satisfacer todas las necesidades de modelado predictivo desde el preprocesamiento hasta la interpretación. Además, su sintaxis también es muy fácil de usar. Si usa R, lo alentaré a que use Caret.

Caret es un paquete muy completo y, en lugar de cubrir todas las funcionalidades que ofrece, pensé que sería una mejor idea mostrar una implementación de extremo a extremo de Caret en un conjunto de datos de hackathon J real. Intenté cubrir tantas funciones en Caret como pude, pero Caret tiene mucho más que ofrecer. Para profundizar, puede que los recursos mencionados anteriormente le resulten muy útiles. Varios de estos recursos han sido escritos por el mismo Max Kuhn (el creador del paquete caret).

Puede poner a prueba sus habilidades y conocimientos. Verificar Competiciones en vivo y compita con los mejores científicos de datos de todo el mundo en los comentarios a continuación.

Relacionado